Навигация
Дифференциальное уравнение относительного движения механической системы
Задание
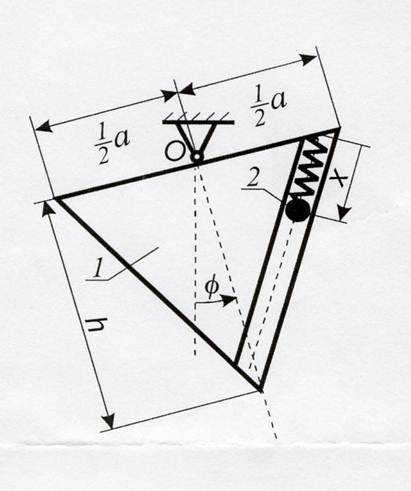
Исходные данные
| Форма тела 1 | Однородная пластина | ||
| Масса тела 1 | m1 | кг | 5 |
| Масса материальной точки 2 | m2 | кг | 0,1 |
| Размеры | a | м | 2 |
| h | м | 3 | |
| Обобщенные координаты | Обозначения | Начальные значения для I этапа | |
| q1 = j | рад | j0 = 0 | |
| q2 = x | м | x0 = 0,8 | |
| Жесткость пружины | с | Н/м | 10 |
| Длина свободной пружины | l0 | м | 0,8 |
| Угловая скорость тела 1 | w1 | рад/c | 4 |
| Конец I этапа движения | t1 | с | 5 |
| Конец II этапа движения | t2 | с | 5 |
Содержание
Введение 1. Поведение системы в условиях стабильного закона движения 2. Поведение системы в конкретных условиях 3. Поведения системы в условиях малых колебаний Список использованной литературыВведение
Изучение теоретической механики как одной из фундаментальных физико-математических дисциплин играет важную роль в подготовке специалистов по механико-математическим и инженерным направлениям. Оно позволяет будущим специалистам не только получить глубокие знания о природе, но и вырабатывает у них необходимые навыки для решения сложных научных и технических задач, для которых требуется построение математических моделей разнообразных механических систем, развивает способности к научным обобщениям и выводам
Теоретическая механика, как часть естествознания, использующая математические методы, имеет дело не с самими материальными объектами, а их математическими моделями. Такими моделями являются материальные точки, системы материальных точек, твердые тела и деформируемая сплошная среда. В курсовой работе рассматриваются простейшие системы, которые состоят из твердых тел, совершающих простейшие движения, и перемещающейся по телу материальной точки.
1. Поведение системы в условиях стабильного закона движения
1.1 Относительное движение материальной точки
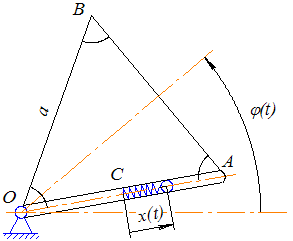
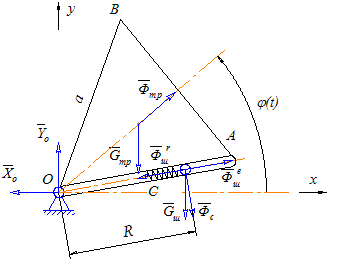
Рис.1 Схема механической системы и действующие на шарик силы
Свяжем подвижную систему координат Оxy с вращающейся пластиной как показано на рисунке.
Вращение пластины вместе с системой координат Oxy вокруг оси является переносным движением для шарика. Относительным движением шарика является его движение вдоль трубки, расположенной вдоль пластины.
Дифференциальное уравнение относительного движения для рассматриваемого случая равномерного вращения пластины имеет вид
![]() , (1.1.1)
, (1.1.1)
где m – масса материальной точки;
![]() - ускорение точки в подвижной системе отсчета;
- ускорение точки в подвижной системе отсчета;
![]() - внешние силы:
- внешние силы: ![]() ,
, ![]()
![]() - реакции связей:
- реакции связей: ![]() -нормальная реакция стенки трубки;
-нормальная реакция стенки трубки;
![]() и
и ![]() - переносная и кориолисова силы инерции.
- переносная и кориолисова силы инерции.
Вращение пластины происходит равномерно, следовательно ![]() =0, значит
=0, значит ![]() -.
-.
Силы инерции ![]() и
и ![]() направлены противоположно переносному центростремительному
направлены противоположно переносному центростремительному ![]() и кориолисову ускорению
и кориолисову ускорению ![]() , соответственно. Направление ускорения
, соответственно. Направление ускорения ![]() определим по правилу Жуковского: необходимо спроектировать относительную скорость шарика в плоскость вращения, а затем повернуть вектор этой скорости на 900 по направлению вращения, и получим направление ускорения Кориолиса.
определим по правилу Жуковского: необходимо спроектировать относительную скорость шарика в плоскость вращения, а затем повернуть вектор этой скорости на 900 по направлению вращения, и получим направление ускорения Кориолиса.
Предположим, что относительная скорость шарика положительна. В этом случае кориолисова сила инерции ![]() направлена параллельно оси Оy подвижной системы координат.
направлена параллельно оси Оy подвижной системы координат.
Модули сил инерции определяются по формулам:
![]() =
=![]()
![]()
![]() =
=![]() .
.
Найдем зависимость he от х:
![]()
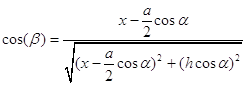
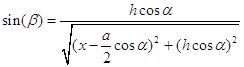
В итоге уравнение (1.1.1) примет вид:
![]()
![]()
Спроектируем векторное уравнение относительного движения шарика на оси подвижной системы координат Оxy:
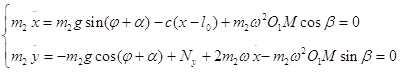 (1.1.2)
(1.1.2)
![]() . Выберем φ0=0 → φ=
. Выберем φ0=0 → φ=![]() ;
; ![]()
Рассмотрим проекцию на ось Ох. Разделим обе части уравнения на массу тела:
![]()
![]() , где
, где ![]()
![]() (1.1.3)
(1.1.3)
Общее решение полученного линейного неоднородного дифференциального уравнения с постоянными коэффициентами будем искать виде
x=X+![]() ,
,
где Х – общее решение соответствующего однородного уравнения,
![]() -частное решение неоднородного уравнения.
-частное решение неоднородного уравнения.
Однородное уравнение имеет вид
![]() =0, (1.1.4)
=0, (1.1.4)
которому соответствует следующее характеристическое уравнение
![]()
![]()
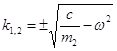 i,
i,
Т.к. величина под корнем отрицательна, то общим решением однородного дифференциального уравнения (1.1.3) будет являться функция:
Х=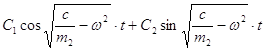 ,
,
где С1 и С2 – постоянные интегрирования.
Частное решение уравнения (1.1.3) будем находить как результат суперпозиции двух решений: ![]() .
.
Для ![]() имеем:
имеем:
![]() (1.1.5)
(1.1.5)
![]() , где
, где ![]() k=0, значит
k=0, значит
![]()
![]()
![]()
Подставим в (1.1.4):
![]()
![]()
При sin![]() :
: ![]()
B=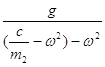
При cos![]() :
: ![]()
A=![]()
Тогда 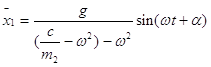
Для ![]() имеем:
имеем:
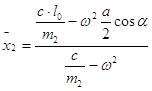
Тогда общее решение дифференциального уравнения относительного движения шарика (1.1.3) принимает вид
x=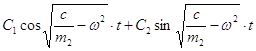
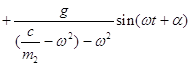
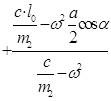
Скорость этого движения равна
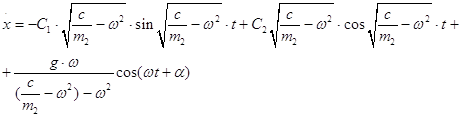
Составляющую реакции стенки трубки Nyопределим из второго уравнения системы (1.1.2)
![]()
где ![]() определяется соответствующим выражением.
определяется соответствующим выражением.
1.2 Закон изменения движущих сил, обеспечивающих заданное движение тела. Реакции внешних опор.
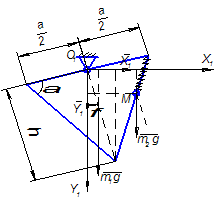
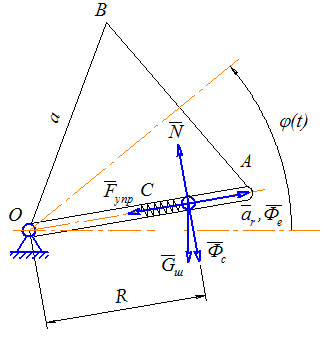
Рис.2 Определение реакций в опорах
Определим проекции реакций опоры на оси неподвижной декартовой системы координат O1x1y1 (рис. 2).
Запишем уравнение теоремы о движении центра масс для рассматриваемой механической системы в векторном виде:
![]() (1.2.1)
(1.2.1)
Проектируя уравнение (2.1) на оси системы координат О1x1y1 получаем
![]() ,
,
![]() (1.2.2)
(1.2.2)
По известным формулам находим координаты центра тяжести системы,
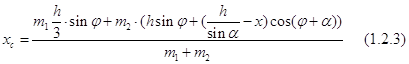
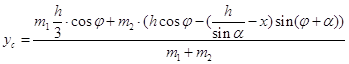 (1.2.4)
(1.2.4)
Дифференцируя уравнения 1.2.3,1.2.4, получим
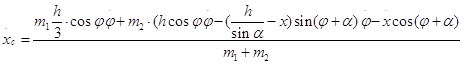
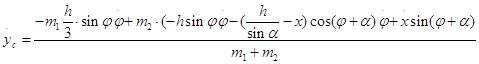
Вычисляя вторые производные получим
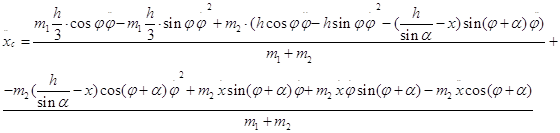
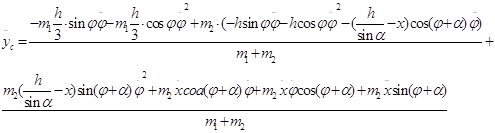 (1.2.5)
(1.2.5)
Подставляя (1.2.5) в уравнения (1.2.2), получаем проекции реакций в опоре О1 на оси неподвижной системы координат:
![]()
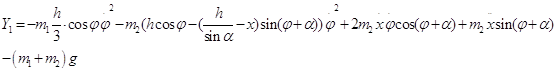
При этом мы учли, что ![]()
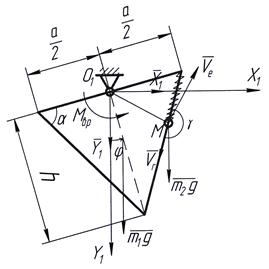
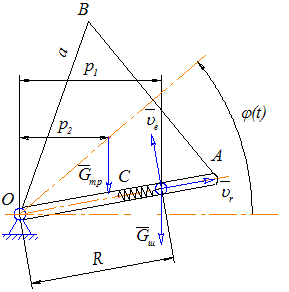
Рис.3 Определение вращательного момента
Применим теорему об изменении кинетического момента для определения внешнего момента, обеспечивающего равномерное движение ведущего звена механической системы. Выберем за ось z ось вращения:
![]() . (1.3.1)
. (1.3.1)
Определим кинетический момент рассматриваемой системы относительно оси Oz.
![]() ,
,
где ![]() - осевой момент инерции пластины,
- осевой момент инерции пластины, ![]() -угловая скорость вращения.
-угловая скорость вращения.
Шарик М совершает сложное движение- относительное вдоль желоба пластины(см. рис.3) со скоростью ![]() и переносное вместе с пластиной. Переносная скорость
и переносное вместе с пластиной. Переносная скорость ![]() перпендикулярна пластине и по модулю равна:
перпендикулярна пластине и по модулю равна:
![]() ,
,
где ![]()
Кинетический момент шарика относительно оси z равен
![]()
![]() ,
,
Кинетический момент всей системы равен
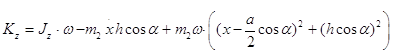 (1.3.2)
(1.3.2)
Определим главный момент внешних сил относительно оси z. Реакции опор ![]() пересекают ось вращения и момент относительно этой оси не создают. Определим момент силы тяжести шарика и пластины:
пересекают ось вращения и момент относительно этой оси не создают. Определим момент силы тяжести шарика и пластины:![]()
![]()
![]()
Отсюда имеем:
![]() , (1.3.3)
, (1.3.3)
где Mвр.- внешний момент, обеспечивающий равномерное вращение пластины.
Подставляя 1.3.2, 1.3.3 в уравнение теоремы об изменении кинетического момента системы 1.3.1, получаем
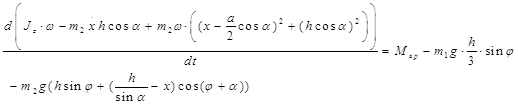 .
.
Учитывая, что ω=const получим:
![]()
Похожие работы
... в шарнире можно найти по формуле: , где и определяются выражениями (4.5) и (4.7); график её зависимости от времени приведён в приложении к курсовой работе (рис. 4). 5. Исследование движения механической системы с двумя степенями свободы с помощью уравнений Лагранжа II рода 5.1 Составление уравнений движения системы методом Лагранжа Уравнения второго рода являются одним из наиболее ...
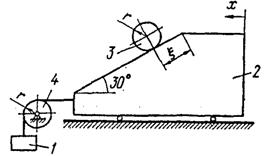
... производные в уравнения Лагранжа (11): или (j=1,2,…, s). (12) Уравнения (12) называются уравнениями Лагранжа второго рода для консервативной системы. 7 Применение уравнений Лагранжа II рода к исследованию движения механической системы Массы тел механической системы m= 2m; m= 6m; m=m. Начальные условия:,,,. Найти уравнения движения системы в обобщенных координатах ,. Для ...
... груза, его скорости и ускорения, а также динамических реакций внешних и внутренних связей. Результаты расчетов: 5. Анализ результатов вычислений Математическая модель, описывающая поведение исследуемой механической системы, построена при следующих основных допущениях: ...
... и реакции внешних и внутренних связей. Произведен численный анализ полученного решения с использованием ЭВМ. Исходные данные: m = 1 кг r = 0.1 м с = 4000 H/м Часть 1. Применение основных теорем динамики механической системы 1.1 Постановка второй основной задачи динамики системы. Расчетная ...
0 комментариев