Навигация
Классификация видов графиков
1.2. Классификация видов графиков.
Существует множество видов графических изображений (рис. 1.1; 1.2) . Их классификация основана на ряде признаков:
а) способ построения графического образа;
б) геометрические знаки, изображающие статистические показатели и отношения;
в) задачи, решаемые с помощью графического изображения.
статистические графики по форме графического образа
| линейные | плоскостные | объемные |
| статистические кривые | - столбиковые - полосовые - квадратные - круговые - секторные - фигурные - точечные - фоновые | поверхности распределения |
Рис. 1.1. Классификация статистических графиков по форме графического образа
статистические графики по способу построения и задачам изображения
диаграммы статистические карты
диаграммы диаграммы картограммы картодиаграммы
сравнения динамики
структурные
диаграммы
Рис. 1.2. Классификация статистических графиков по способу построения и задачам изображения
По способу построения статистические графики делятся на диаграммы и статистические карты. Диаграммы - наиболее распространенный способ графических изображений. Это графики количественных отношений. Виды и способы их построения разнообразны. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т. д. При этом сравнение исследуемых совокупностей производится по какому-либо существенному варьирующему признаку. Статистические карты - графики количественного распределения по поверхности. По своей основной цели они близко примыкают к диаграммам и специфичны лишь в том отношении, что представляют собой условные изображения статистических данных на контурной географической карте, т. е. показывают пространственное размещение или пространственную распространенность статистических данных. Геометрические знаки, как было сказано выше, - это либо точки, либо линии или плоскости, либо геометрические тела. В соответствии с этим различают графики точечные, линейные, плоскостные и пространственные (объемные).
При построении точечных диаграмм в качестве графических образов применяются совокупности точек; при построении линейных - линии. Основной принцип построения всех плоскостных диаграмм сводится к тому, что статистические величины изображаются в виде геометрических фигур и, в свою очередь, подразделяются на столбиковые, полосовые, круговые, квадратные и фигурные.
Статистические карты по графическому образу делятся на картограммы и картодиаграммы.
В зависимости от круга решаемых задач выделяются диаграммы сравнения, структурные диаграммы и диаграммы динамики.
ГЛАВА 2. ДИАГРАММЫ.
2.1. Диаграммы сравнения.
Наиболее распространенными диаграммами сравнения являются столбиковые диаграммы, принцип построения которых состоит в изображении статистических показателей в виде поставленных по вертикали прямоугольников - столбиков. Каждый столбик изображает величину отдельного уровня исследуемого статистического ряда. Таким образом, сравнение статистических показателей возможно потому, что все сравниваемые показатели выражены в одной единице измерения.
При построении столбиковых диаграмм необходимо начертить систему прямоугольных координат, в которой располагаются столбики. На горизонтальной оси располагаются основания столбиков, величина основания определяется произвольно, но устанавливается одинаковой для всех.
Шкала, определяющая масштаб столбиков по высоте, расположена по вертикальной оси. Величина каждого столбика по вертикали соответствует размеру изображаемого на графике статистического показателя. Таким образом, у всех столбиков, составляющих диаграмму, переменной величиной является только одно измерение (пример 1).
Размещение столбиков в поле графика может быть различным:
- на одинаковом расстоянии друг от друга;
- вплотную друг к другу;
- в частном наложении друг на друга.
Правила построения столбиковых диаграмм допускают одновременное расположение на одной горизонтальной оси изображений нескольких показателей. В этом случае столбики располагаются группами, для каждой из которых может быть принята разная размерность варьирующих признаков (пример 2).
Разновидности столбиковых диаграмм составляют так называемые ленточные или полосовые диаграммы. Их отличие состоит в том, что масштабная шкала расположена по горизонтали сверху и она определяет величину полос по длине (пример 3).
Область применения столбиковых и полосовых диаграмм одинакова, так как идентичны правила их построения. Одномерность изображаемых статистических показателей и их одномасштабность для различных столбиков и полос требуют выполнения единственного положения: соблюдения соразмерности (столбиков - по высоте, полос - по длине) и пропорциональности изображаемым величинам. Для выполнения этого требования необходимо: во-первых, чтобы шкала, по которой устанавливается размер столбика (полосы) , начиналась с нуля; во-вторых, эта шкала должна быть непрерывной, т.е. охватывать все числа данного статистического ряда; разрыв шкалы и соответственно столбиков (полос) не допускается. Невыполнение указанных правил приводит к искаженному графическому представлению анализируемого статистического материала.
Столбиковые и полосовые диаграммы как прием графического изображения статистических данных, по существу, взаимозаменяемы, т.е. рассматриваемые статистические показатели равно могут быть представлены как столбиками, так и полосами. И в этом, и в другом случае для изображения величины явления используется одно измерение каждого прямоугольника - высота столбика или длина полосы. Поэтому и сфера применения этих двух диаграмм в основном одинакова.
Разновидностью столбиковых (ленточных) диагармм являются направленные диаграммы. Они отличаются от обычных двусторонним расположением столбиков или полос и имеют начало отсчета по масштабу в середине. Обычно такие диаграммы применяются для изображения величин противоположного качественного значения. Сравнение между собой столбиков (полос), направленных в разные стороны, менее эффективно, чем расположенных рядом в одном направлении. Несмотря на это, анализ направленных диаграмм позволяет делать достаточно содержательные выводы, так как особое расположение придает графику яркое изображение. К группе двусторонних относятся диаграммы чистых отклонений. В них полосы направлены в обе стороны от вертикальной нулевой линии: вправо - для прироста; влево - для уменьшения. С помощью таких диаграмм удобно изображать отклонения от плана или некоторого уровня, принятого за базу сравнения. Важным достоинством рассматриваемых диаграмм является возможность видеть размах колебаний изучаемого статистического признака, что само по себе имеет большое значение для анализа (пример 4).
Для простого сравнения не зависимых друг от друга показателей могут также использоваться диаграммы, принцип построения которых состоит в том, что сравниваемые величины изображаются в виде правильных геометрических фигур, которые строятся так, чтобы площади их относились между собой как количества, этими фигурами изображаемые. Иными словами, эти диаграммы выражают величину изображаемого явления размером своей площади.
Для получения диаграмм рассматриваемого типа используют разнообразные геометрические фигуры - квадрат, круг, реже - прямоугольник. Известно, что площадь квадрата равна квадрату его стороны, а площадь круга определяется пропорционально квадрату его радиуса. Поэтому для построения диаграмм необходимо сначала из сравниваемых величин извлечь квадратный корень. Затем на базе полученных результатов определить сторону квадрата или радиус круга соответственно принятому масштабу.
Наиболее выразительным и легко воспринимаемым является способ построения диаграмм сравнения в виде фигур-знаков. В этом случае статистические совокупности изображаются не геометрическими фигурами, а символами или знаками, воспроизводящими в какой-то степени внешний образ статистических данных. Достоинство такого способа графического изображения заключается в высокой степени наглядности, в получении подобного отображения, отражающего содержание сравниваемых совокупностей.
Важнейший признак любой диаграммы - масштаб. Поэтому чтобы правильно построить фигурную диаграмму, необходимо определить единицу счета. В качестве последней принимается отдельная фигура (символ), которой условно присваивается конкретное численное значение. А исследуемая статистическая величина изображается отдельным количеством одинаковых по размеру фигур, последовательно располагающихся на рисунке. Однако в большинстве случаев не удается изобразить статистический показатель целым количеством фигур. Последнюю из них приходится делить на части, так как по масштабу один знак является слишком крупной единицей измерения. Обычно эта часть определяется на глаз. Сложность точного ее определения является недостатком фигурных диаграмм. Однако большая точность представления статистических данных не преследуется, и результаты получаются вполне удовлетворительными (пример 5).
Как правило, фигурные диаграммы широко используются для популяризации статистических данных и рекламы.
Похожие работы
... по действующей программе. Раздел III. Статистика предприятий и перерабатывающих производств в системе АПК должна изучаться студентами всех специальностей. Изучение этого раздела статистики служит основой для изучения отраслевой экономики, организации и планирования производства и изучения рынка труда, предпринимательства, анализа хозяйственной деятельности и ряда других экономических дисциплин. ...
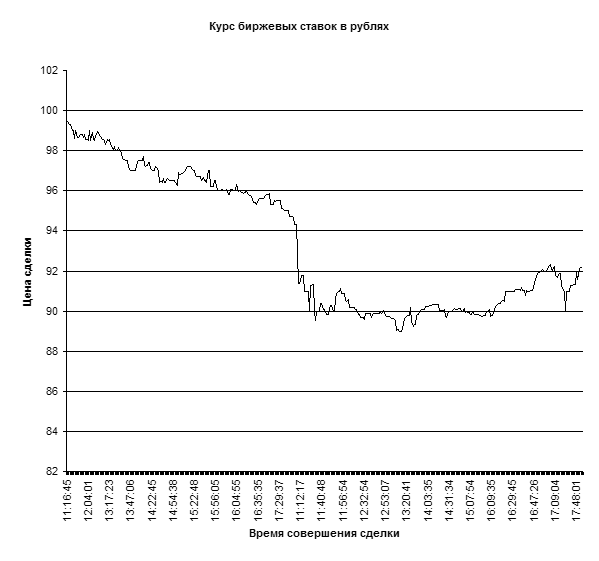
... быстро выполняемой счетной операцией. Данная работа посвящена изучению возможности обработки статистических данных биржевых ставок методами корреляционного и регрессионного анализа с использованием пакета прикладных программ Microsoft Excel. Роль корреляцонно-регрессионного анализа в обработке экономических данных Корреляционный анализ и регрессионный анализ являются смежными разделами ...
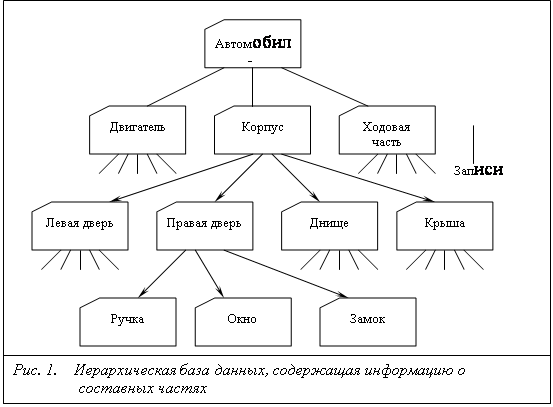
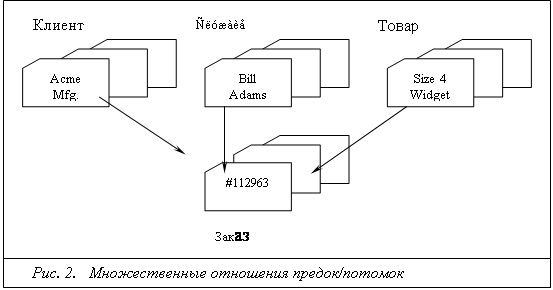
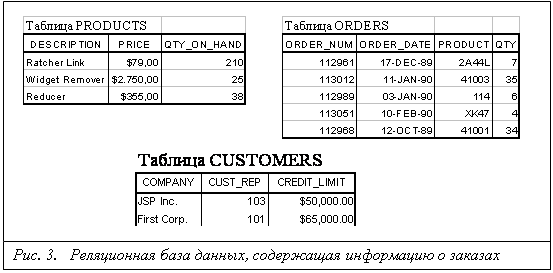
... ЭВМ. Приложения, созданные с помощью SQL и рассчитанные на однопользовательские системы, по мере своего развития могут быть перенесены в более крупные системы. Информация из корпоративных реляционных баз данных может быть загружена в базы данных отдельных подразделений или в личные базы данных. Наконец, приложения для реляционных баз данных можно вначале смоделировать на экономичных персональных ...
... интересует. Соблюдение принципа наглядности – одно из основных требований, которому должно удовлетворять обучение математике в начальных классах. В начальных классах эффективно использовать технические средства обучения (ТСО) и наглядность по несколько минут на различных этапах урока. В процессе работы важно применять технические средства обучения в комплексе с другими средствами наглядности, ...


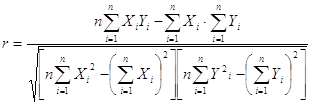


0 комментариев