Навигация
Множественная корреляция
2.3. Множественная корреляция
Проведенный выше анализ статистических совокупностей позволяет изучить взаимосвязь только двух переменных.
На практике же часто приходится исследовать зависимость результирующего признака от нескольких факторных признаков. В этом случае статистическая модель может быть представлена уравнением регрессии с несколькими переменными. Такая регрессия называется множественной (множественная корреляция).
Например, линейная регрессия с m независимыми переменными имеет вид:
yi = a0x0 + a1x1 + a2x2 + … + amxm, (2.1)
где а0, а1, а2, …, аm – параметры уравнения регрессии,
m – число независимых переменных,
х0, х1, х2, …, хm – значения факторного признака,
yi – значение результирующего признака.
При оценке параметров этого уравнения в каждом i-том наблюдении фиксируют значения результирующего признака у и факторных признаков хi0…хim.
Оценки параметров уравнения регрессии находятся с помощью метода наименьших квадратов, который в случае множественной регрессии удобнее представить в матричной форме.
Применяются следующие обозначения:
а = (аj), j = 0,1,…,m – вектор оценок параметров, m – число неизвестных параметров;
у = (уi), i = 1,2,…,n – вектор значений зависимой переменной, n – число наблюдений;
х = (хij) – матрица значений независимых переменных размерностью n(m+1);
е = (ei) – вектор ошибок в уравнении с оцененными параметрами.
Уравнение регрессии с оцененными параметрами имеет вид:
у = Ха, (2.2)
Линейная модель (2.1) в векторном виде имеет вид:
у = Ха + е. (2.3)
Сумма квадратов отклонений равна:
Q = åеi2 = eTe = (y-Xa)T(y-Xa) = yTy – aTXTy – yTXa + aTXTXa =
= yTy – 2aTXTy + aTXTXa, (2.4)
где Т – знак операции транспонирования, т.е. строки исходной матрицы в транспонированной занимают положение столбцов.
Дифференцированием Q по а получается
= -2ХТу + 2(ХТХ)а (2.5)
Приравниванием производной к нулю получается выражение для определения вектора оценки а:
ХТу = ХТХа,
а = (ХТХ)-1(ХТу). (2.6)
Оценку а, определенную изложенным способом, называют оценкой метода наименьших квадратов. Применительно к уравнению регрессии (2.1) матрицы коэффициентов имеют вид:
I x11 x12 … x1m
I x21 x22 … x2m
X = … … … … … ,
… … … … …
I xn1 xn2 … xnm
и, следовательно,
n åxi1 … åxim
åхi1 åxi12… åxi1xim
XTX= … … … … ,
… … … …
åхim åxi1xim … åxim2
åуi
åyixi1
ХТу= : .
:
åyixim
Суммирование производится по числу наблюдений n.
2.4. Применение множественной корреляции к изучению состава кадров на промышленном предприятии
Рассматривается пример:
Переменная у (заработная плата) зависит от разряда х1 и степени выплачивания норм х2 . Принимая линейную модель множественной регрессии в виде
y=a0+a1x1=a2x2
определить оценки а0, а1, а2 параметров по методу наименьших квадратов.
Исходные данные по 30 рабочим приведены в табл. 2.3.
Таблица 2.3.
Сведения о заработной плате, стажу и степени выполнения норм по 30 рабочим на промышленном предприятии
| i | y, зар.плата | x1, разряд | x2, степень вып. норм |
| 1 | 2 | 3 | 4 |
| 1 | 1100,1 | 5 | 117,4 |
| 2 | 1121,3 | 5 | 118,3 |
| 3 | 700,5 | 3 | 102,4 |
| 4 | 801,5 | 5 | 113,7 |
| 5 | 714,5 | 4 | 101,5 |
| 6 | 1500,5 | 7 | 127,5 |
| 7 | 1100,9 | 6 | 118,4 |
| 8 | 575,8 | 4 | 97,4 |
| 9 | 1598,5 | 7 | 134,5 |
| 10 | 704,5 | 4 | 98,5 |
| 11 | 714,5 | 4 | 101,5 |
| 12 | 763,1 | 4 | 109,4 |
| 13 | 670,4 | 2 | 121,3 |
| 14 | 764,3 | 4 | 117,4 |
| 15 | 1307,4 | 7 | 129,7 |
| 16 | 800,4 | 5 | 118,6 |
Продолжение табл.2.3.
| 1 | 2 | 3 | 4 |
| 17 | 619,7 | 4 | 103,3 |
| 18 | 1607,4 | 7 | 136,7 |
| 19 | 614,1 | 6 | 114,9 |
| 20 | 691,8 | 4 | 100,3 |
| 21 | 576,4 | 3 | 100,9 |
| 22 | 900,7 | 5 | 99,6 |
| 23 | 587,3 | 6 | 105,4 |
| 24 | 814,4 | 6 | 103.7 |
| 25 | 767,5 | 5 | 111,1 |
| 26 | 1409.5 | 7 | 127,3 |
| 27 | 1499,7 | 7 | 129,9 |
| 28 | 904,4 | 6 | 117,7 |
| 29 | 871,3 | 5 | 105,4 |
| 30 | 860,5 | 5 | 103,2 |
| Итого | 152 | 3386,9 |
Оценки а0, а1, а2 следует рассчитать по методу наименьших квадратов.
1 5 117,4 1100,1 1 … 1
X = : : : , Y = : , XT = 5 … 5
1 5 103,2 860,5 117,4 … 103,2
30 152 3386,9 27662,9
XTX = 152 824 17466 , XTy = 150068,4 ,
3386,9 17466 38632,4 3215384
0,004570565 -0,000891327 2,27457Е-06
(XTX)-1 = -0,000891327 0,000172501 1,53416Е-07 .
2,27457Е-06 1,53416Е-07 –3,37237Е-07
Вектор оценок параметров уравнения линейной регрессии равен (см.формулу 2.6.) :
-0,01133
а = 42,08981 .
7,313614
Уравнение линейной регрессии с данными оценками параметров имеет следующий вид:
у = -0,01133 + 42,08981*х1 + 7,313614*х2.
Далее следует проводить анализ коэффициентов регрессии.
2.5.Анализ коэффициентов регрессии
В общем случае, чтобы сделать коэффициенты регрессии сопоставимыми, применяют нормированные коэффициенты регрессии.
Коэффициент показывает величину изменения результативного признака в значениях средней квадратичной ошибки при изменении факторного признака хj на одну среднеквадратическую ошибку:
(2.7)
где аj – коэффициент регрессии при факторе хj;
j – 1,2,…,m; m – число факторных признаков;
- среднеквадратическое отклонение факторного признака хj;
- среднеквадратическое отклонение результативного признака.
Для множественной регрессии также определяются частные коэффициенты эластичности Эj относительно хj:
(2.8)
где - частная производная от регрессии по переменной хj;
хj – значение фактора хj на заданном уровне;
у – расчетное значение результативного признака при заданных уровнях факторных признаков.
Коэффициент Эj показывает, на сколько процентов изменится результативный признак при изменении факторного признака на 1 процент при фиксировании значений остальных факторов на каком-либо уровне. Если в качестве такого уровня принять их средние значения, то получаем средний коэффициент эластичности.
По данным рассматриваемого примера имеются следующие оценки:
Среднее квадратическое
отклонение: х1=1,3; х2=11,5; у=30,4.
Среднее: х1=5; х2=112,9; у=922,1.
- коэффициент: 1=1,8; 2=2,8.
Эластичность: Э1=0,241; Э2=0,96.
Из анализа полученных результатов по коэффициенту эластичности вытекает, что в среднем второй фактор (степень выполнения норм) в 3,9 раз сильнее влияет на результат (заработную плату), чем первый (разряд):
Э2/Э1=0,96/0,24=3,9 ,
Анализ же уравнений регрессии по нормированным коэффициентам j показывает, что второй фактор влияет сильнее всего лишь в 1,5 раза ( 1/ 2=1,5), т.е. нормированный коэффициент определяет факторных признаков на результат более точно, т.к. он учитывает вариации факторов.
ЗАКЛЮЧЕНИЕ
Изучив методы статистического анализа, а именно: метод группировки и корреляционный анализ ( парный и множественный ) и применив полученные знания к изучению состава кадров на промышленном предприятии, можно сделать следующие выводы.
С помощью типологической группировки по профессии выявляется следующая тенденция: большинство рабочих на данном промышленном предприятии являются помощниками бурильщиков ( 37% ), что составляет огромный потенциал для дальнейшего профессионального роста и расширения деятельности данной организации.
Структурная группировка по разряду работников характеризует персонал как среднеквалифицированный, т.к. наблюдается наличие большого количества работников 4 и 5 разрядов ( 54%), в то время как работники 6 и 7 разрядов составляют лишь 37% , а низкоквалифицированные (2 и 3 разряды) – 9%.
Группировка работников по стажу показывает, что большинство работников имеет стаж от 2 до 5 лет ( 33%) и стаж от 5 до 8 и от 8 до 11 лет по 20%. Также наблюдается тенденция к снижению работников с высоким стажем, что подтверждает гистограмма распределения работников по стажу (см. рис.1.1).
Парный корреляционный анализ позволил обнаружить зависимость заработной платы от стажа: с увеличением стажа работников увеличивается их заработная плата, хотя работники со стажем 5-8 лет и 8-11 лет получают в среднем одинаковую заработную плату (915 т.р.), также как и работники со стажем в интервале 14-17 лет и свыше 17 лет ( их заработная плата 1515 т.р.).
Это подтверждает таблица, составленная из группировки работников по стажу и соответствующих каждому интервалу средних значений заработной платы (см.табл.2.2).
Многофакторный анализ зависимости зарплаты от степени выполнения норм и разряда работников показывает, что степень выполнения норм влияет на заработную плату в 1,5 раза сильнее, чем разряд работников (при использовании нормированного коэффициента анализа уравнений регрессии).
Таким образом, использование методов группировки и корреляционного анализа позволило провести исследование состава кадров на промышленном предприятии. Основываясь на полученных выводах, можно повысить уровень работы с персоналом, а следовательно косвенно увеличить производительность труда и степень выполнения норм работниками, что особенно важно в условиях постоянно меняющейся экономической ситуации.
СПИСОК ЛИТЕРАТУРЫ
1. Герчук Я.П. Графики в математическо-статистическом анализе. – М.: Статистика, 1972.
2. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – М.:ИНФРА-М, 1996.
3. Кильдишев Г.C., Аболенцев Ю.И. Многомерные группировки. – М.: Статистика, 1978.
4. Общая теория статистики : учебник / Под.ред. А.А.Спирина. – М.: Финансы и статистика, 1996.
5. Сиськов В.И. Корреляционный анализ в экономических исследованиях. – М.: Статистика, 1975.
6. Теория статистикки : учебник /Под.ред. Р.А.Шмойловой. – М.: Финансы и статистика, 1996.
Приложение 1 Состав рабочих на промышленном предприятии
| № | ФИО | Профессия | Разряд | Степень выполнения норм, % | Стаж, лет | Зарплата,т.р. |
| 1 | Алексеев | Бурильщик | 5 | 117,4 | 8 | 1100,1 |
| 2 | Антонов | Бурильщик | 5 | 118,3 | 8 | 1121,3 |
| 3 | Бердяев | Проходчик | 3 | 102,4 | 5 | 700,5 |
| 4 | Воронин | Взрывник | 5 | 113,7 | 4 | 801,5 |
| 5 | Державин | Пом.бурильщика | 4 | 101,5 | 4 | 714,5 |
| 6 | Дронин | Бурильщик | 7 | 127,5 | 17 | 1500,5 |
| 7 | Дьячнов | Проходчик | 6 | 118,4 | 9 | 1100,9 |
| 8 | Жилин | Проходчик | 4 | 97,4 | 0,8 | 575,8 |
| 9 | Княжев | Взрывник | 7 | 134,5 | 19 | 1598,5 |
| 10 | Корлев | Пом.бурильщика | 4 | 98,5 | 2 | 704,5 |
| 11 | Косин | Пом.бурильщика | 4 | 101,5 | 7 | 714,5 |
| 12 | Ламин | Пом.бурильщика | 4 | 109,4 | 7 | 763,1 |
| 13 | Марков | Горнорабочий | 2 | 121,3 | 5 | 670,4 |
| 14 | Москвин | Проходчик | 4 | 117,4 | 4 | 764,3 |
| 15 | Носов | Взрывник | 7 | 129,7 | 6 | 1307,4 |
| 16 | Осипов | Пом.бурильщика | 5 | 118,6 | 4 | 800,4 |
| 17 | Пахомов | Пом.бурильщика | 4 | 103,3 | 3 | 619,4 |
| 18 | Петров | Бурильщик | 7 | 136,7 | 16 | 1607,4 |
| 19 | Порохов | Взрывник | 6 | 114,9 | 4 | 614,1 |
| 20 | Родге | Пом.бурильщика | 4 | 100,3 | 2 | 691,8 |
| 21 | Рылин | Пом.бурильщика | 3 | 100,9 | 2 | 576,4 |
| 22 | Светлов | Бурильщик | 5 | 99,6 | 4 | 900,7 |
| 23 | Тихинов | Взрывник | 6 | 105,4 | 7 | 587,3 |
| 24 | Торопов | Проходчик | 6 | 103,7 | 10 | 814,4 |
| 25 | Уфимов | Проходчик | 5 | 111,1 | 11 | 767,5 |
| 26 | Френкель | Бурильщик | 7 | 127,3 | 12 | 1409,5 |
| 27 | Фролов | Бурильщик | 7 | 129,9 | 15 | 1499,5 |
| 28 | Хвостов | Пом.бурильщика | 6 | 117,7 | 11 | 904,4 |
| 29 | Цветов | Пом.бурильщика | 5 | 105,4 | 10 | 871,3 |
| 30 | Яров | Пом.бурильщика | 5 | 103,2 | 10 | 860,5 |
Похожие работы
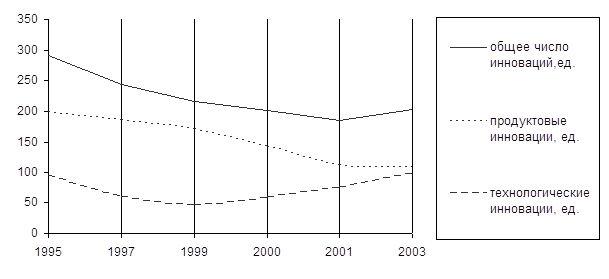
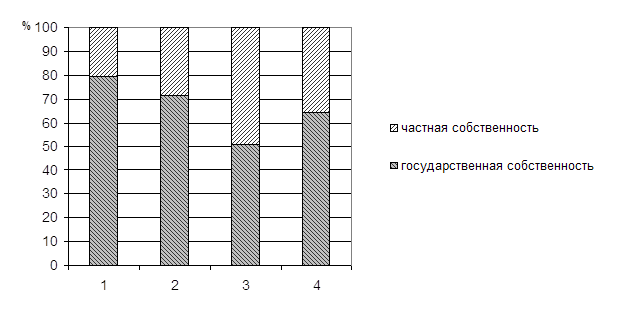
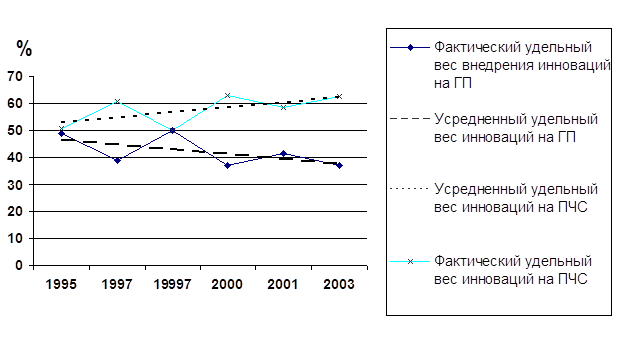
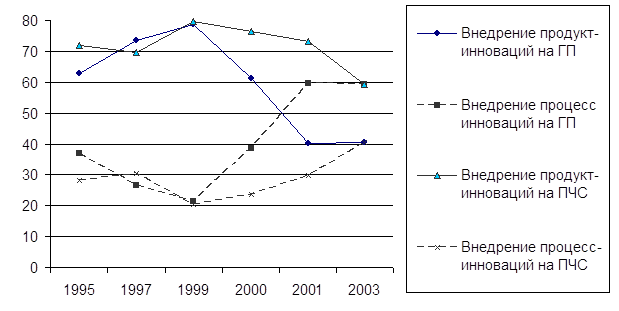
... деятельности они значительно уступают предприятиям частной формы собственности. ГЛАВА III РАЗРАБОТКА МЕТОДОВ ОПРЕДЕЛЕНИЯ РЕЗЕРВОВ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ИННОВАЦИОННОЙ ДЕЯТЕЛЬНОСТИ ПРОМЫШЛЕННЫХ ПРЕДПРИЯТИЙ 3.1. Обоснование резервов повышения эффективности инновационной деятельности и их классификация Технический уровень и эффективность промышленного производства в будущем определяются ...
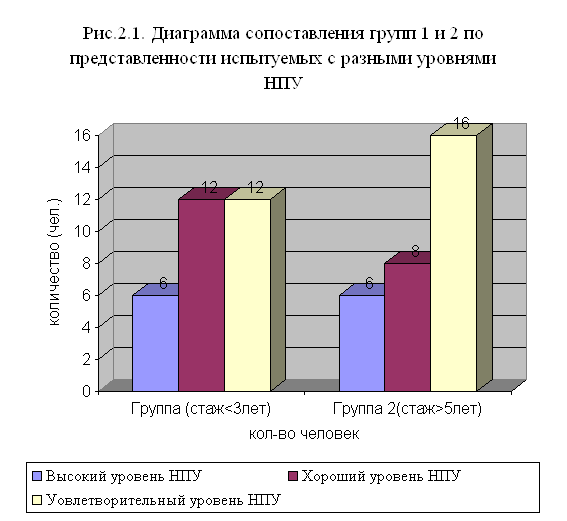
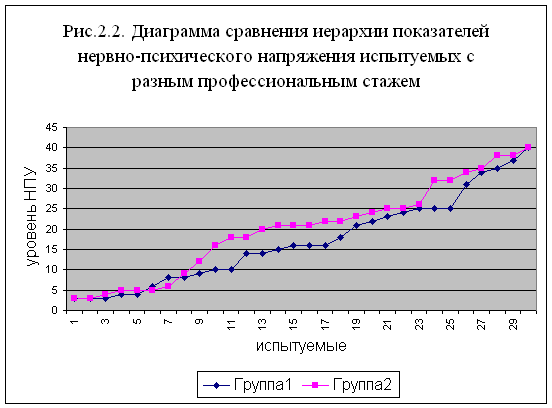
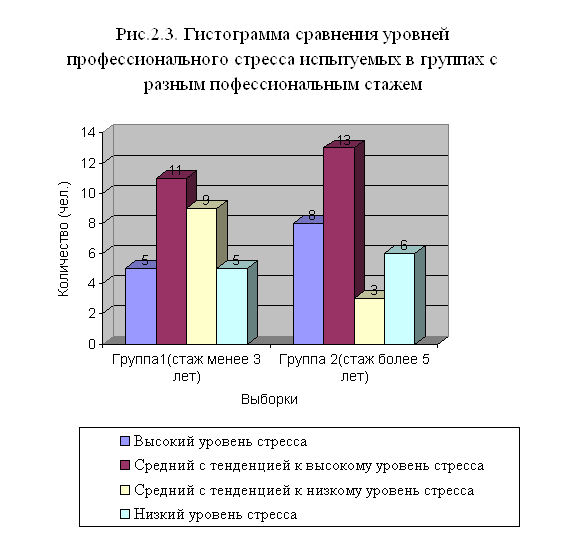
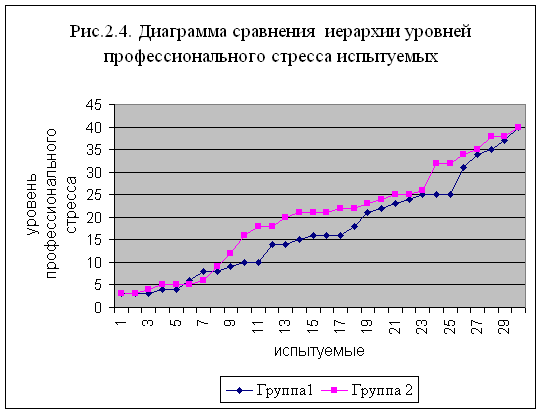
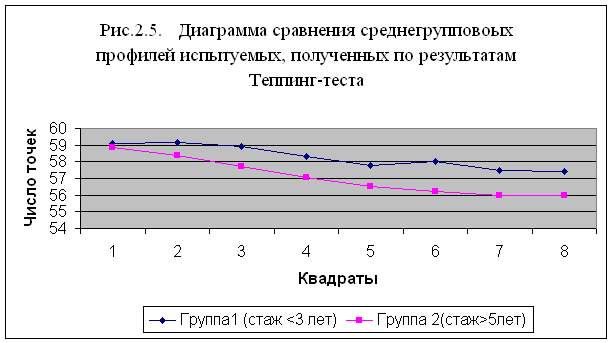
... особенностей мужчин, работающих на вредном производстве, от профессионального стажа. 2.1.Ход и организация исследования. Цель работы: изучение зависимости стрессоустойчивости, психофизиологических особенностей мужчин, работающих в условиях промышленного предприятия, от профессионального стажа. Гипотезой исследования стало предположение о существовании зависимости уровня стрессоустойчивости от ...
... выявление резервов и неиспользованных возможностей на предприятии, разработка мероприятий по приведению их в действие. 2. Анализ состава, структуры и обеспеченности предприятия трудовыми ресурсами 2.1. Анализ состава и структуры кадров Обеспеченность предприятия трудовыми ресурсами определяется сравнением фактического количества работников по категориям и профессиям в отчетном году с ...
... принятых за период работников; Чнеув – численность уволенных за период работников по неуважительной причине; Чсж - численность уволенных за период работников по собственному желанию. Глава 2 Анализ кадров в кафе «Гора» 2.1 Исходные данные Кафе «Гора» расположено на окраине города, по адресу улица Малиновая, дом 1а. В здании с общей площадью 67 квадратных метров. Кафе начало свою работу ...
0 комментариев