Навигация
Описание программной реализации
2 Описание программной реализации
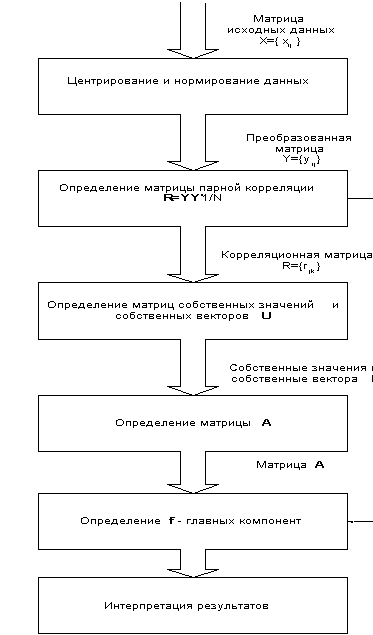
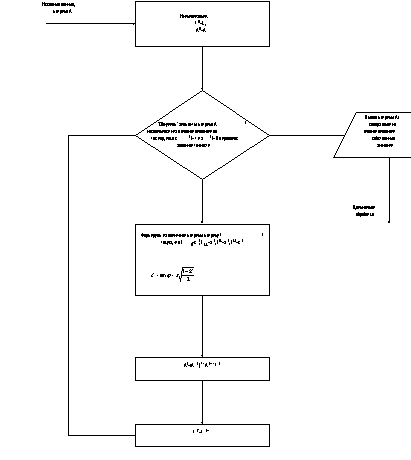
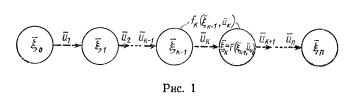
Программа для реализации метода главных компонент была написана на языке Turbo Pascal 7.0. Все вычисления выполнены в последовательности, представленной на рисунке 1.1. Обозначения программных переменных и массивов по возможности соответствуют изложенным выше. Программа является в достаточной степени универсальной, т.к. приспособлена для обработки массивов данных любой размерности (их размер ограничен только объемом доступной памяти). Однако в программе не предусмотрен ввод данных с клавиатуры. Размерность массивов задана константами, а массив исходных данных инициализируется также в теле программы. При необходимости ввода других данных можно легко скорректировать исходный текст программы.
Отдельной процедурой в программе описан вывод на экран матрицы m*m. В программе часто приходится проделывать эту операцию, поэтому она оформлена как процедура out.
Первой процедурой является центрирование и нормирование исходных данных. Оно выполняется в соответствии с описанными выше формулами.
Далее запрограммировано нахождение коэффициентов характеристического уравнения для корреляционной матрицы R. Оно производится в соответствии с рекуррентными соотношениями Фаддеева, т.е по следу матриц, производных из R, по формулам:
Ai-1=ABi-2; Pi-1=1/(m-1)trAi-1; Bi-1=Ai-1-Pi-1E; i=1,2..m. (2.1)
После вычисления рекуррентных соотношений находится характеристический полином:
Pm(λ)= λm - P1 λm-1 - P2 λm-2 -…- Pm. (2.2)
Известно, что при m > 4 (2.2) не имеет общего решения. Однако мы знаем, что это уравнение имеет все вещественные корни, и что их число равно m. Для их нахождения используется итерационный метод Ньютона, поскольку исследуемая функция – полином и нет затруднений в вычислении ее производной. Итерационная формула Ньютона для i-й точки имеет вид:
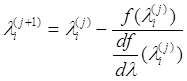 , (2.3)
, (2.3)
где j – номер итерации.
Далее в соответствии с (1.1) находим собственные векторы матрицы R. Для решения систем уравнений применялся метод Гаусса. Однако предварительно необходимо было исключить одно неизвестное. Для этого переменным umj были присвоены единичные значения, последний столбец перенесен в правую часть с обратным знаком, а последнее уравнение исключено из рассмотрения.
После получения матрицы собственных векторов U было проведено ее нормирование, в результате чего была получена матрица нормированных собственных векторов V.
Затем вычисляется матрица факторного отбражения A в соответствии с правилами умножения матриц.
Далее находится матрица, обратная к A, методом m-кратного пересчета элементов [3,с.358] по рекуррентным формулам:
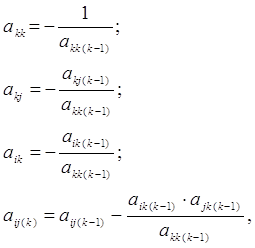
где k – номер итерации, k=1..m. На заключительном этапе A-1 = -A(k).
После нахождения матрицы, обратной A, находим матрицу F – матрицу факторного отображения и выводим ее на экран в транспонированном виде в соответствии с (1.2). На этом расчеты по методу главных компонент завершены.
ЗАКЛЮЧЕНИЕВ данной курсовой работе была построена математическая модель и программная реализация метода главных компонент. Следует отметить, что в работе не была рассмотрена методика отсева несущественных факторов, и поэтому результирующая модель, выдаваемая программой на экран, содержит число компонент, равное числу исходных элементарных признаков m. К достоинствам разработанной программы можно отнести то, что она может работать с массивами исходных данных достаточно большой размерности.
ЛИТЕРАТУРА1 Сошникова Л.А., Тамашевич В.Н., Уебе Г., Шебер М. Многомерный статистический анализ в экономике: Учеб. Пособие для вузов/Под ред. проф. Тамашевича. – М.: ЮНИТИ-ДАНА, 1999. –598с.
2 А. Епанешников, В. Епанешников. Программирование в среде Turbo Pascal 7.0. –3-е изд., стер. –М.: “ДИАЛОГ-МИФИ”, 1997. –288с.
3 Жуков Л.А., Стратан И.П. Установившиеся режимы сложных электрических сетей и систем: Методы расчетов. –М.: Энергия, 1979. – 416 с.
ПРИЛОЖЕНИЕ АТекст программы метода главных компонент
Program gl_komp;
const
m=3;{число признаков}
n=4;{число объектов}
type
matrix=array[1..m,1..m]of real;
var
x,z:array[1..n,1..m]of real;
f:array[1..m,1..n]of real;
a_,b_,_a_,_b_:matrix;{для алгоритма Фаддеева}
c:array[1..m-1,1..m-1]of real;
d:array[1..m-1]of real;
l,r,u,a,a_1,v:matrix;
p:array[0..m]of real;
i,j,k,q:integer;
s,x_,b,_b,w:real;
{-------процедура вывода на экран матрицы m*m----------}
procedure out(t:matrix);
var
i1,j1:integer;
begin
for i1:=1 to m do
begin
for j1:=1 to m do
write(' ',t[i1,j1]:3:3,' ');
writeln
end
end;
{===================================================================}
Begin
writeln('ПРОГРАММА РАСЧЕТА ГЛАВНЫХ КОМПОНЕНТ ПО ЗАДАННОМУ РАСПРЕДЕЛЕНИЮ');
writeln;
x[1,1]:=2;x[1,2]:=1.3;x[1,3]:=0.55;x[2,1]:=4;x[2,2]:=1.42;x[2,3]:=5.1
x[3,1]:=1.1;x[3,2]:=5.3;x[3,3]:=0.55;x[4,1]:=2.14;x[4,2]:=5.12;x[4,3]:=1.9;
{------стандартизуем значения признаков-----------}
for j:=1 to m do
begin
{----находим среднее и сигму-----}
s:=0;x_:=0;
for i:=1 to n do
s:=s+x[i,j];
x_:=s/n;s:=0;
for i:=1 to n do
s:=s+(x[i,j]-x_)*(x[i,j]-x_);
s:=sqrt(s/n);
{------нормируем-------}
for i:=1 to n do
z[i,j]:=(x[i,j]-x_)/s
end;
{---------находим матрицу парных корреляций R=(1/n)*Z'*Z----------}
for j:=1 to m do
for i:=1 to m do
begin
s:=0;
for k:=1 to n do
s:=s+z[k,j]*z[k,i];
r[j,i]:=s/n
end;
{-------------выводим матрицу R------------}
writeln('Матрица парных корреляций R:');
out(r);
{-------=====находим собственные числа матрицы R======----------}
{-----приравниваем R и _a_-------}
for i:=1 to m do
for j:= 1 to m do
_a_[i,j]:=r[i,j];
p[1]:=3;{т.к на главной диагонали единицы}
for i:=1 to m do
for j:=1 to m do
if i<>j
then
_b_[i,j]:=_a_[i,j]
else
_b_[i,j]:=-2;
for q:=2 to m do
{----вычисляем p[q] и определитель-----}
begin
{----вычисляем A[q]----}
for i:=1 to m do
for j:=1 to m do
begin
s:=0;
for k:= 1 to m do
s:=s+r[i,k]*_b_[k,j];
a_[i,j]:=s
end;
{------вычисляем p[q]-------}
s:=0;
for i:=1 to m do
s:=s+a_[i,i];
p[q]:=s/q;
{----вычисляем B[q]-----}
for i:=1 to m do
for j:=1 to m do
if i<>j
then
b_[i,j]:=a_[i,j]
else
b_[i,j]:=a_[i,j]-p[q];
{----присваиваем предыдущим переменным значения текущих-----}
for i:= 1 to m do
for j:=1 to m do
begin
_a_[i,j]:=a_[i,j];
_b_[i,j]:=b_[i,j]
end
end;
{---------===решаем характеристическое уравнение===----------}
p[0]:=1;
for i:=1 to m do
p[i]:=-p[i];
for i:=1 to m do
for j:=1 to m do
l[i,j]:=0;
{------задаем начальные приближения------}
for i:=1 to m do
l[i,i]:=-p[i]/p[i-1];
{------выполняем итерационный процесс по методу Ньютона--------}
repeat
w:=0;
for i:=1 to m do
begin
b:=0;_b:=0;
{-----вычисляем значение полинома в i-й точке-------}
for j:=0 to m do
begin
s:=1;
for k:=0 to m-j-1 do
s:=s*l[i,i];
b:=b+p[j]*s
end;
{------находим максимальную невязку-------}
if b>w then
w:=b;
{------вычисляем значение производной в i-й точке------}
for j:=0 to m-1 do
begin
s:=1;
for k:=0 to m-j-2 do
s:=s*l[i,i];
_b:=_b+(m-j)*p[j]*s
end;
{------вносим поправку для i-й точки-------}
l[i,i]:=l[i,i]-(b/_b)
end
{----выходим из процесса при достижении требуемой точности----}
until w<0.0001;
{-------выводим собственные числа на экран---------}
writeln('Собственные числа матрицы R:');
for i:=1 to m do
writeln('L[',i,'] := ',l[i,i]:3:3);
{-----======находим матрицу собственных векторов u======---------}
{-----последним компонентам придаем единичные значения-----}
for i:= 1 to m do
u[m,i]:=1;
{------==решаем m систем уравнений==------}
for q:=1 to m do
begin
{----заполняем левые части-----}
for i:=1 to m-1 do
for j:=1 to m-1 do
if i=j
then
c[i,j]:=1-l[q,q]
else
c[i,j]:=r[i,j];
{----заполняем правые части-----}
for i:=1 to m-1 do
d[i]:=-r[i,m]*u[m,i];
{---------решаем систему методом Гаусса-----------}
i:=1;
{-------------прямой ход---------------}
repeat
{---нормируем элементы i-й строки---}
d[i]:=d[i]/c[i,i];
for j:=m-1 downto i do
c[i,j]:=c[i,j]/c[i,i];
{----делаем нули под ведущим элементом----}
for k:=i+1 to m-1 do
begin
d[k]:=d[k]-d[i]*c[k,i];
for j:=m-1 downto i do
c[k,j]:=c[k,j]-c[i,j]*c[k,i]
end;
i:=i+1
until i=m;
{------------обратный ход-------------}
u[m-1,q]:=d[m-1];
for i:=m-2 downto 1 do
begin
u[i,q]:=d[i];
for j:=i+1 to m-1 do
u[i,q]:=u[i,q]-u[j,q]*c[i,j]
end
end;
{------нормируем собственные векторы - находим матрицу v---------}
for j:=1 to m do
begin
s:=0;
for i:=1 to m do
s:=s+u[i,j]*u[i,j];
for i:=1 to m do
v[i,j]:=u[i,j]/sqrt(s)
end;
{--выводим нормированную матрицу собственных векторов на экран---}
writeln('Матрица нормированных собственных векторов V:');
out(v);
{---------находим матрицу факторного отображения a----------}
for i:=1 to m do
for j:=1 to m do
begin
s:=0;
for k:=1 to m do
s:=s+v[i,k]*sqrt(l[k,j]);
a[i,j]:=s
end;
{--------выводим матрицу факторного отображения---------}
writeln('Матрица факторного отображения A:');
out(a);
{===находим матрицу, обратную a, методом m-кратного пересчета===}
for k:=1 to m do
{-----цикл пересчета-----}
begin
for i:=1 to m do
for j:=1 to m do
if (i=k) or (j=k)
then
if i=j
then
a_1[i,j]:=-1/a[i,j]
else
a_1[i,j]:=-a[i,j]/a[k,k]
else
a_1[i,j]:=a[i,j]-a[i,k]*a[k,j]/a[k,k];
for i:=1 to m do
for j:=1 to m do
a[i,j]:=a_1[i,j]
end;
for i:=1 to m do
for j:=1 to m do
a_1[i,j]:=-a[i,j];
{------===находим матрицу значений главных компонент F===-------}
for i:=1 to m do
for j:=1 to n do
begin
s:=0;
for k:=1 to m do
s:=s+a_1[i,k]*z[j,k];
f[i,j]:=s
end;
{-------выводим матрицу F на экран в транспонированном виде-------}
writeln('Матрица значений главных компонент F:');
for i:=1 to n do
begin
for j:=1 to m do
write(' ',f[j,i]:3:3,' ');
writeln
end;
writeln;
readln;
End.
Похожие работы
... , необходимых для разработки и эксплуатации задач. ГЛАВА 2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ КОМПЛЕКСА ЗАДАЧ "ОЦЕНКА ЭФФЕКТИВНОСТИ ФУНКЦИОНИРОВАНИЯ ВОЕННО-МЕДИЦИНСКОГО УЧРЕЖДЕНИЯ” 2.1 Постановка задачи и её спецификация Основной целью разработки КЗ “Оценка эффективности работы военного госпиталя методом главных компонент” является автоматизация обработки статистических данных, представляющих собой ...
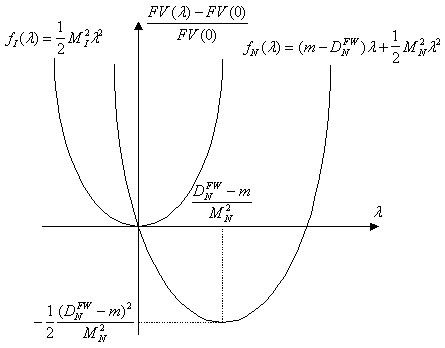
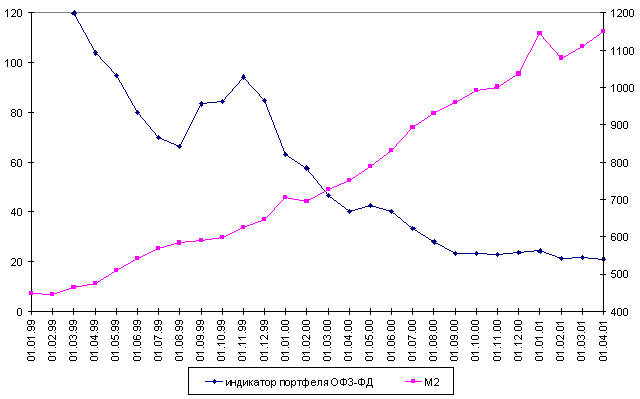
... параметров в случае резкого перехода к новой рыночной ситуации. Глава 2. Обоснование методов поддержки принятия решений по управлению процентным риском портфеля ГКО–ОФЗ в посткризисный период. §2.1. Иммунизация процентного риска портфеля ГКО–ОФЗ от непараллельных перемещений временной структуры процентных ставок. Процентный риск владельца портфеля облигаций существенно зависит от того, в какой ...
... параметрами, показателями объекта именно в то время. Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени. Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в ...
... на них, оценки технико-экономических показателей и, в завершении, построения экономико-математической модели предприятия. В экономико-математической модели в целевую функцию должен вводиться тот или иной фактор неопределенности. В дальнейшем будет приведена разработка методика учета факторов неопределенности, показаны математические модели снятия неопределенности. Крайне важным является оценка ...
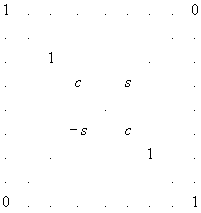
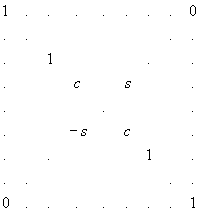

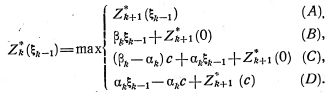
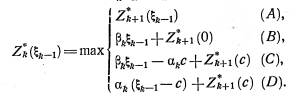
0 комментариев