Навигация
Функциональные (хар-ся точностью и полнотой охвата)
1. Функциональные (хар-ся точностью и полнотой охвата).
2. корреляционные.
При (1) каждому значению величины факторного признака (Х) соответствует только 1 строго определенное значение результативного признака (У). Причем размер этого изменения можно точно определить в каждом определенном случае и для каждое единицы совокупности. Чаще всего такие связи рассматриваются точными науками.
Массовые явления общественной жизни хар-ся многообразием факторов, из взаимосвязью => результативный признак может изменяться под влиянием этих факторов.
Связь м/у факторными и результативными признаками будет неполной и будет проявляться лишь в средней. Это – корреляционные связи (хар-ся тем, что сред вел. результативного признака измен-ся под воздействием изм-я многих факторных признаков.
Корреляционные связи проявляются в массе общественных явлений
Связи м/у явлениями подразделяются в зависимости от направления движения на нарямые и обратные.
прямые: направление изменения результативного признака совп. с напр. изм-я факторного.
обратные: если фактор. признак растет, то результ. понижается.
Выявление связей м/у признаками определяется на основе корреляционного метода, где корреляция («соотношение») характеризует взаимозависимость 2-х случайных величин Х и У, показывая влияние одного или нескольких факторов на изуч. процесс.
В ходе корреляционного анализа выявляется теснота связи. Показателем, характеризующим форму и тесноту связи явл. линейный k-т корреляции (r).
r = ((xy)ср. – xср.yср.)/(dxdy)
r<0 – связь обратная
rà+-1 – св. тесная
r=0,5 – св. средняя
rà0 – св. слабая
r=1 – не корр. зависимость, а функциональная.
Если установлена форма связи и определена теснота => опр-ся корр. зависимость м/у факт. и результативным признаком (регрессия). Это зависимость какой либо сл. вел. от др. вел. Эта зависимость закл. в поиске теоретич. линий связи (линии регрессии).
Математически эта связь представлена уравнением прямой Ух = Ао + А1Х (линейное ур-е связи).
Ао, А1 – параметры, кот надо определить.
Ао – нач значение результативного признака, не завис. от факторного.
А1 – k-t регрессии, показывающий, на сколько ед-ц изменяется сред. значение результативного признака с изменением факторного признака на ед.
Пример: Ух = 15,4 +0,8х
Зависимость: прибыль (у) – стоимость осн. фондов (х)
0,8 – если увел. ст-ть ОФ на 1, то прибыль возр. на 0,8.
Ух – теоретическое значение результативного признака.
На основе а1 рассчитыв-ся k-т эластичности, кот. показывает изменение результативного признака в % с изменением факторного признака на 1%.
Э = а1хср./уср.
Чтобы рассчитать а1 и а0 нужно решить сис-му нормированных уравнений.
/ а0т + а1Sх = Sу
\ а0Sх + а1Sх2 = Sху
Расчет параметров ур-я позволяет определить теоретическое значение результативного признака.
Правильность решения можно установить на основе S-х значений Sу и Sух (фактич. и теорет.). Они не должны сильно различаться (Sу @ Sух). Тогда корреляционный анализ проведен правильно, параметры рассчитаны ровно и правильно выявлена зависимость м/у факт. и рез. признаками.
Выборочное наблюдение. Расчет ошибки выборки.
- это наблюдение, при котором кар-ку всей сов-ти получают на основе некоторой части этой совокупности, отобр. в случайном, непреднамеренном порядке.
Выборочная сов-ть – часть сов-ти, кот. подверг. исслед-ю.
Генеральная – вся сов-ть, из которой производится отбор. На ее основе опр. долю выборки.
(ск-ко % нужно выбрать) d=n/N n – выборочн. N – генер.
Не совпад. качественных характеристик м/у генеральными и выборосными сов-тями – ошибка выборки (ошибка репрезентативности).
Основная задача выборочного набл-я – расчет изменения Х (Dх).
t – k-т кратности ошибки (показ., сколько сред. ошибок содержится в предел. ошибке выборки).
Dх = tm
m - сред. ошибка выборки.
Пределы возможной ошибки опр-ся в вероятностью появления этих ошибок, где t находится по таблице интеграла вероятности.
t = 1 p = 0,683
t = 2 p = 0,954
t = 3 p = 0,997
m зависит от выборочной совокупности (n) – чем > n, тем < ошибка.
m зависит от колеблемости (показателей вариации) – чем больше отклонение от средней, тем больше ошибка
Нужно различать повторную и безповторную выборки.
повторная: m = d/Ön (Ö-кв. корень)
безповторная: m = Öd2/n(1-n/N)
Похожие работы
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... измерений на рабочем месте. Чтобы эти службы эффективно выполняли стоящие перед ними задачи необходимо научное, техническое и правовое обеспечение их деятельности. Научной основой МО является метрология - наука об измерениях. Техническую основу МО составляют: система государственных эталонов единиц ФВ; система передачи размеров единиц ФВ от эталонов всем средствам измерений с помощью образцовых ...
... их можно периодически менять, делая вид, что сломался карандаш или кончилась ручка. Один юный талант умудрился на ручке иголкой нацарапать ответы на все вопросы теоретического экзамена в ГАИ. Сигареты - шпаргалки помешаются в патроны сигарет, вместо табака. На сигаретах можно проставит номера билетов или краткое название темы вопроса. Пачка сигарет помещается на стол и лежит там в течении всего ...
... ее в рукав пиджака. Причем прикрепляют шпору на резинке. Держат бумажку в ладони и списывают. А как только на горизонте показался преподаватель, просто отпускают ее, и шпаргалка самостоятельно “запрыгивает” обратно. Бывают, конечно, и более изощренные виды шпаргалок. Алексей М., студент факультета социологии СПбГУ, смастерил для сдачи экзаменов волшебную ручку — с увеличительным стеклышком. ...
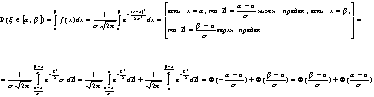


0 комментариев