Навигация
Методы формообразования поверхностей
1.2. Методы формообразования поверхностей.
а) Метод копирования.
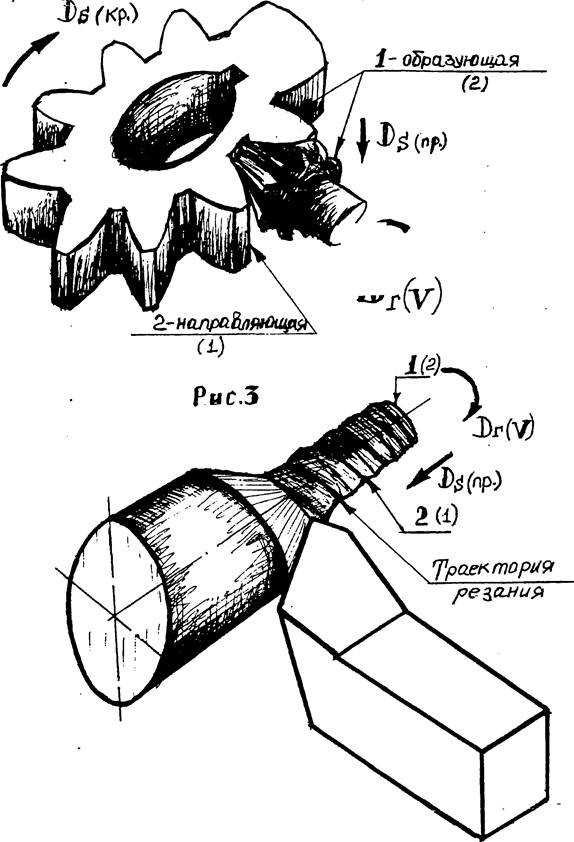
Этот метод состоит в том, что режущая кромка инструмента соответствует форме образующей обрабатываемой поверхности детали (рис 3). Направляющая линия 2 воспроизводится перемещением заготовки
относительно инструмента. Главное движение здесь является формообразующим. Движение подачи необходимо для того, чтобы получить геометрическую поверхность определённого размера. Метод копирования широко используют при обработке фасонных поверхностей детали на различных металлорежущих станках.
б) Метод следов.
Этот метод состоит в том, что образующая линия 1 является проекцией (следом) траектории движения точки (вершины) режущей кромки инструмента или траектории результирующего движения резания на плоскость вектора Ds(пр), а направляющая линия 2 проекцией (следом) этой же траектории на плоскости вектора Dг (рис 4). Оба движения резания формообразующие.
в) Метод касания.
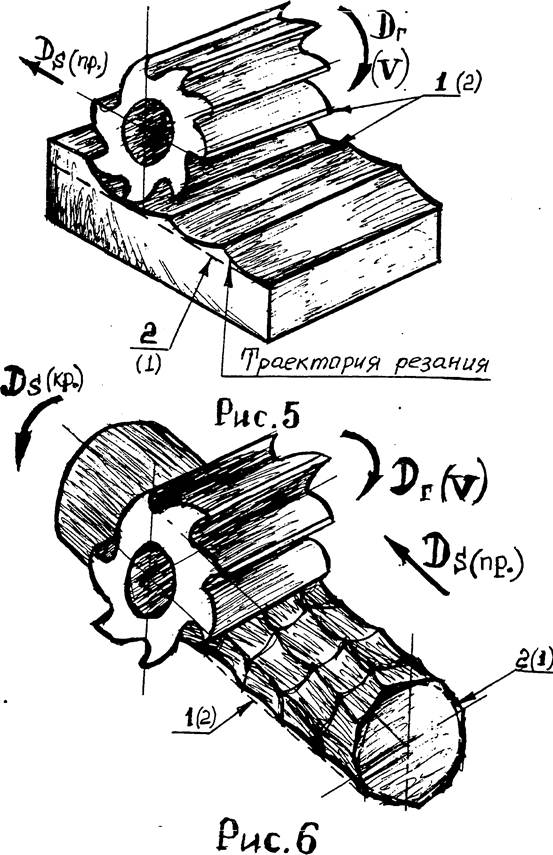
Образующей линией 1 служит режущая кромка инструмента (рис 5), а направляющая линия 2 поверхности касательная к ряду геометрических вспомогательных линий - траекториям точек режущей кромки инструмента. здесь формообразующим является только движение подачи. г) Метод обкатки (огибания).
.Направляющая линия 2 воспроизводится вращением заготовки (рис 6).
9
2. Определение новых способов механической обработки из принцнпиалыю - возможных и выбор наиболее эффективных с помощью ЭВМ.
2.1. Метод систематического определения новых эффективных
способов механической обработки.
Любой процесс обработки поверхности детали инструментом определяет кинематическая схема резания или формообразования. Уже в 40-х годах в работе Грановского Г.И. была дана классификация схем резания. Было установлено, что получение заданной геометрической формы поверхности возможно путем различных сочетаний вращательной и поступательных движений изделия и инструмента. Движения, сообщаемые механизмом станка, как инструменту, так и детали могут быть выражены принципиальными кинематическими схемами резания. В соответствии с принятой принципиальной кинематической схемой резания режущие элементы инструмента в процессе резания перемещаются относительного рабочего движения со скоростями, предопределяемыми кинематическим соотношением: инструмент изделия. На этом основании обработанные поверхности имеют своими образующими траектории относительного рабочего движения. Вследствие этого внешние, очертания контура обработанных поверхностей выражают характер последних на всем их протяжении или соответствующих отдельных участках. Отсюда следует, что с изменением принципиальной кинетической схемы резания и кинематического соотношения инструмент - изделие изменяются характер траектории и величина скорости относительно рабочего движения и одновременно с этим также и очертания образуемого им контура обрабатываемого изделия На основании изложенного Грановским Г.И. был предложен метод систематизации возможных схем обработки, данный в виде схем характеристических движений, которые были построены на основе двух элементарных движений, прямолинейного и вращательного.
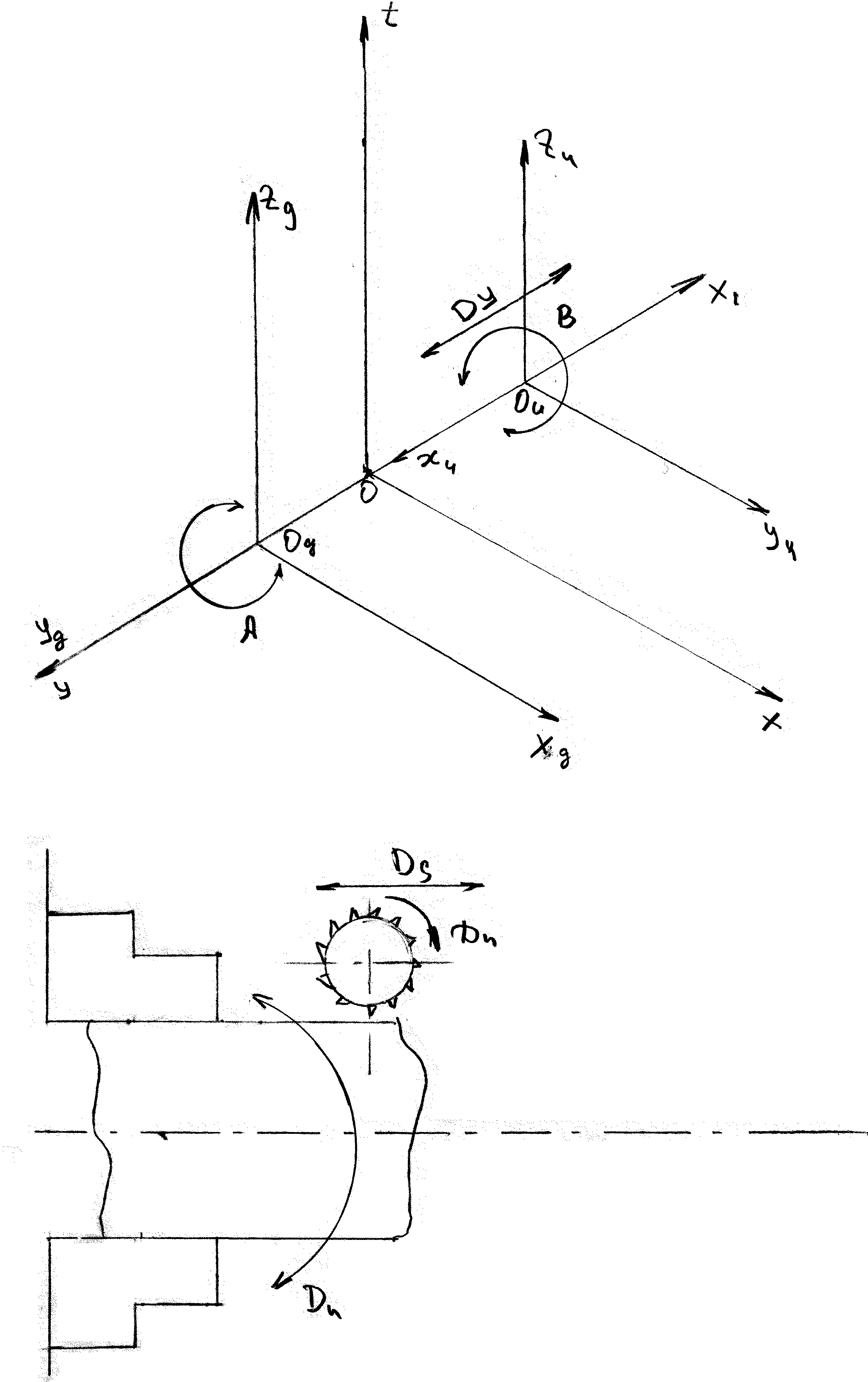
Позднее в работе Коновалова Е.Г. был проведен анализ всех 8 групп кинематических схем резания таблицы, разработанной Грановским Г.И. Было установлено, что различие принципиальных кинематических схем резания основано на движениях обрабатываемой детали и инструмента. Разнообразные сочетания движений детали и инструмента образуют ту или иную схему или группы схем. Общность всех схем заключается в движении детали и инструмента. Так например, любое прямолинейное пространственное движение можно представить в виде движений по трем взаимно-перпендикулярным осям. Коноваловым Е.Г. было сделано заключение, что простые движения входящие в состав элементарных кинематических схем резания, по существу своему представляют часть сложного движения, входящего в .общую универсальную схему, в которой обрабатываемая деталь имеет в своей системе координат (ХоУоZо) три вращения и три поступательных движения вокруг и вдоль осей. Режущий инструмент также имеет в своей системе координат {Х2Y2Z2) аналогичные движения. Любая кинематическая схема резания, представляет собой лишь частный случай такой универсальной схемы. Используя выдвинутые положения, представим универсальную кинематическую схему формообразования в виде, изображенном на рис. 7. Предложенная схема несколько отличается от универсальной схемы Коновалова Е.Г. Однако, она ни в коей мере не теряет универсальности в результате следующих соображений, а именно. Любая кинематическая схема может .определить траекторию
12
относительного движения точки тела при движении двух систем вдоль существующих движений, поэтому наиболее сложная траектория движения может быть определена шестью степенями свободы или шестью движениями твердого тела в пространстве. Кроме того, два любых вращения в системах (ХоУоZо) и (Х2Y2Z2) при формообразовании по схеме Коновалова Е.Г. будут определять один относительный поворот систем в пространстве, величина которого зависит только от соотношения движений. Поэтому целесообразно два движения заменить одним, имеющим любую пространственную ориентировку по отношению к какой-либо временно неподвижной системе ХоУоZo. Аналогично следует поступить с прямолинейным движением.
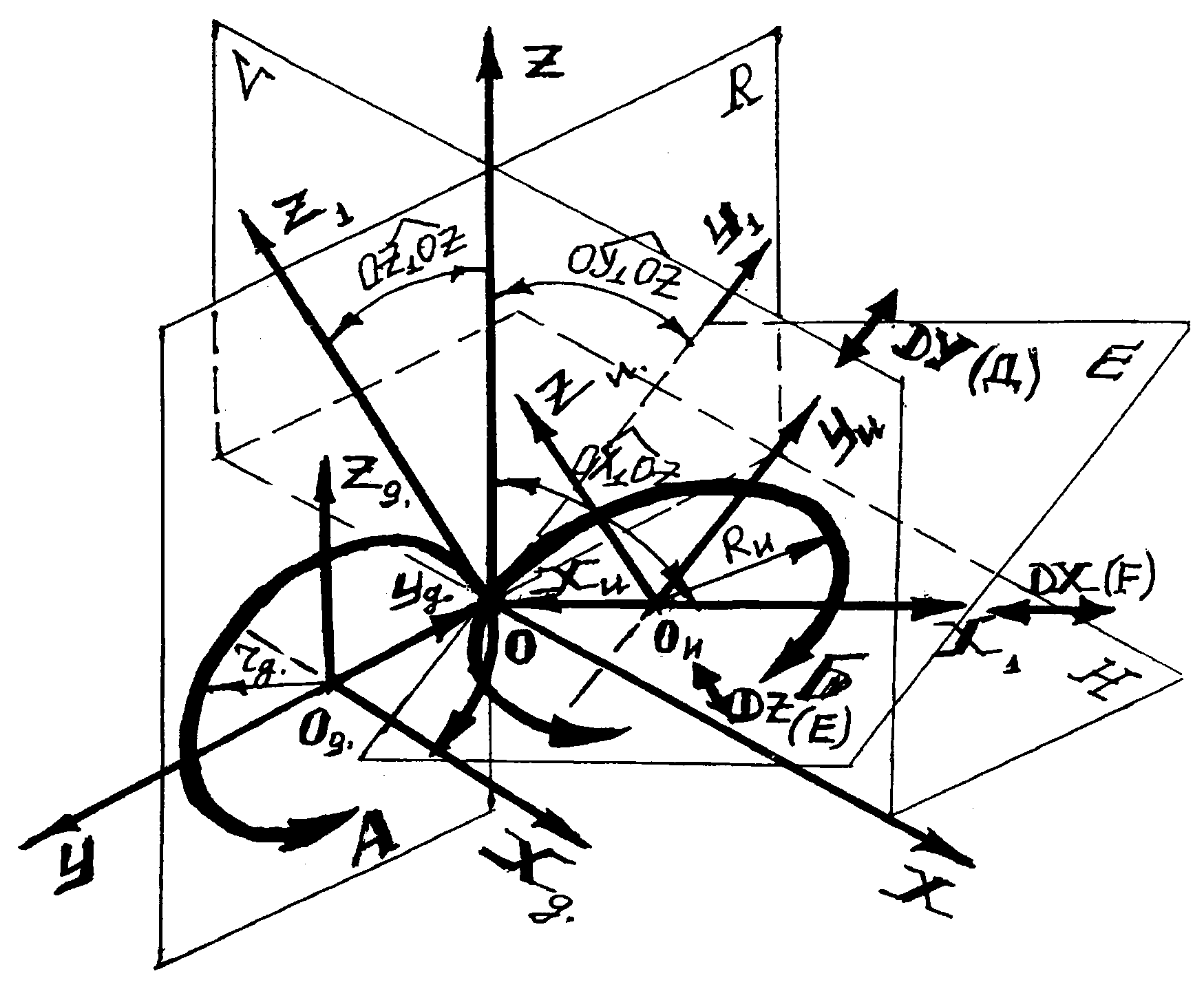
Остановимся более подробно на построении общей кинематической схемы (рис 7.). Так как многообразие способов обработки достигается за счет комбинации движений, сообщаемых инструменту и заготовке, изменения величин скоростей, составляющих движений, и их взаимного расположения и направления, то универсальная кинематическая схема построена по следующему принципу. В схеме предусмотрена вспомогательная неподвижная прямоугольная система координат ХУZ с основными плоскостями R,V,H. Зафиксирована система координат детали ХоУоZо параллельная система ХУZ и удаленная от ее центра по оси ОY на произвольную величину радиуса г (движения вращения А), зависящую от размеров детали, определяющих положение теоретических точек обрабатываемой поверхности при принятой схеме базирования детали, контактирующих с режущей кромкой инструмента в точке О в исходной момент формообразования. При этом система координат ХоУоZо является исходной временно неподвижной системой, так как в основной ее плоскости R предусмотрено существование вращательного движения А, осуществляемого вокруг оси ОХ.
Временно неподвижные или подвижные системы координат Х1Y1Z1 и Х2У2Z2 Из них, система координат Х2У2Z2 является исходной системой координат инструмента. Она параллельна системе X1Y1Z1 и удалена от ее центра - контактной точки О по оси O1Х1 на произвольную величину радиуса К (движения вращения Б), зависящую от конструкций инструмента, и определяющую положение точки режущей кромки, контактирующей с теоретической поверхность детали в исходный момент формообразования. Промежуточная система координат детали и инструмента, зависящее от величин пространственных углов поворота системы X1Y1Z1 относительно ХУZ.
Таким образом, в универсальной кинематической схеме все разнообразие вариантов формообразования поверхностей при принятых схемах базирования деталей в системе ХоУоZо определяется шестью относительными движениями систем координат детали и инструмента, а именно:
а) равномерными вращениями подвижных систем координат по стрелкам А и Б при любом направлении вращения .
б) тремя равномерными поступательными движениями в направлении стрелок В,F,D в подвижной системе координат Х1У1Z1 при изменении направления каждого движения в противоположные стороны.
Общей схемой предусмотрсно вращение инструмента относительно лишь одной оси, но если учесть, что система инструмента может быть расположена в пространстве как угодно, (принимаемые значения пространственных углов), то тем самым и можно считать заданным существование третьего движения вращения всей системы инструмента вокруг системы детали с центром вращения в контактной точке О, определяемое изменением значения одного из углов.
13
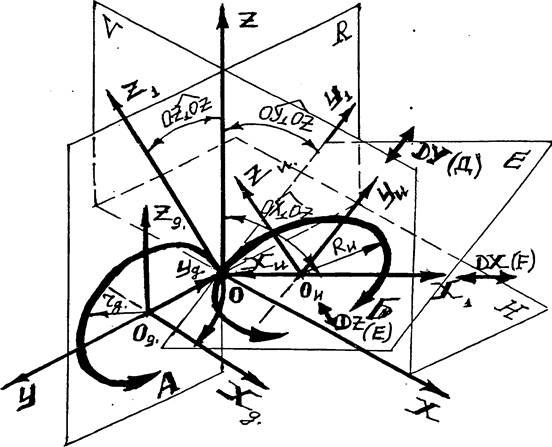
Рис. 7 Универсальная схема формообразования произвольной поверхности детали
Используя основные положения теории формообразования поверхностей инструментами, изложенные в работе [1] покажем, что все процессы формообразования различных поверхностей деталей машин имеют кинематическое единство. Поэтому каждый конкретный способ формообразования той или иной поверхности является лишь частным случаем формообразования какой-то произвольной поверхности и может быть рассмотрен в общем виде при использовании наиболее сложных кинематических схем резания или схем формообразования.
Согласно указанной теории режущий инструмент обрабатывает поверхность контактным способом и в процессе обработки выполняет две функции, резание и формообразование. Поэтому перемещение режущей кромки в процессе формообразования должно быть связано с таким рабочим движением, при котором обеспечивается хотя бы ее периодическое касание с номинальной (теоретически заданной) поверхностью.
С другой стороны, для выполнения функции резания движение кромки должно таким, чтобы припуск на номинальной поверхности детали срезался слоями, по заданному закону. В связи с этим, для удаления всего припуска инструмент должен сделать серию движений резания, благодаря которым его режущая кромка (или кромки, производящей поверхности инструмента, расположенные по линии криволинейной координаты Г) создает семейство поверхностей резания, где каждая последующая поверхность резания смещена относительно предыдущей. Движение инструмента, вызывающее такое смещение поверхностей резания, называется подачей, поэтому: параметр подачи является параметром семейства поверхностей резания.
Инструмент может иметь несколько подач. Каждая подача вызывает образование семейства поверхностей резания. При большом числе подач режущая кромка инструмента может создать очень сложную систему семейств поверхностей резания. При любой такой системе для процесса формообразования поверхности имеют значения только те подачи, которые определяют перемещение по номинальной поверхности детали точки касания режущей кромки при образовании семейств поверхностей резания. Закон, по которому создана система одного или нескольких семейств поверхностей резания, определяет схема резания или схема формообразования, так как она задает уравнение движения режущей кромки как линии или твердого тела в пространстве.
Сложность кинематической схемы формообразования определяется количеством подач инструмента, которое зависит от наличия составляющих движений, указанных на схеме.
Таким образом, наличие всех движений на универсальной кинематической схеме будет определять закон расположения поверхностей резания в пространстве, который в свою очередь будет задавать траекторию движения формообразования. Так как характер траектории связан с соотношением движений, выполняемых режущей кромки, то ее вид остается произвольным в системе координат ХоУо2о. Любая номинальная поверхность детали в той же системе может быть задана также произвольно. Двумя линиями криволинейных координат g и n, которые для одной и той же поверхности могут быть выбраны в весьма широких пределах.
Будем рассматривать процесс формообразования поверхности множеством Zu и кромок. Тогда, с геометрических позиций, множество кромок может быть определено в системе инструмента также линией криволинейной координаты f, а производящая поверхность инструмента будет задана двумя
линиями криволинейных координат f и i, где f есть ни что иное, как линия режущей кромки. Линия криволинейной координаты производящей поверхности инструмента Г выполняет функцию абсолютного рабочего движения формообразования, т.е. обеспечивает дополнительное перемещение кромки относительно формируемой поверхности детали. Закон расположения кромок на производящей поверхности инструмента примем неизвестным. Тогда функцию перемещения точки кромки по линии криволинейной координаты будет выполнять кинематическая схема формообразования.
Траектория, образованная на номинальной поверхности детали точечным контактом с режущими кромками при движении формообразования (заданном кинематической схемой резания), может быть рассмотрена как любая криволинейная координатная линия номинальной поверхности § (или п). Следовательно, выбирая абсолютные движения резания и движения подач на общей схеме резания, процесс формообразования номинальной поверхности детали о геометрических позиций можно рассматривать в общем виде, определив в системе координат детали ХоУоZо произвольные линии криволинейных координаты g и n.
Известно, что некоторые поверхности могут иметь криволинейную координатную линию, которая замыкается в пространстве на самой поверхности (как например - винтовая линия тел вращения). Такая криволинейная координатная линия номинальной поверхности детали всегда является пространственной линией, точки которой на номинальной поверхности могут быть представлены в любом порядке, следовательно, она может определять любые другие линии криволинейных координат § и п.
Таким образом, выбираемые сочетания элементарных движений, их направления и соотношения величин будут определять условия трансформации универсальной схемы в любую конкретную схему формообразования. Проверка условия принадлежности контактных точек семейств поверхностей резания формируемой, номинальной поверхности детали будет определять пригодность той или иной схемы формообразования для получения заданной поверхности при принятой схеме, базирования детали или принятом, фиксированном положении поверхности в системе координат ХоУоZо. Множество схем резания из принципиально-возможных для формообразования заданной поверхности будет определятся не только от выбора линий g и n. Так например, если режущая кромка инструмента совпадет (точнее конгруэнтна) с выбранной на номинальной поверхности детали какой-либо криволинейной координатной линией g (или n), то для формирования поверхности достаточно одно движение резания при отсутствии каких-либо подач. Здесь возможен вариант определяющий "холостую" подачу, т.о. существование вспомогательного перемещения инструмента по линию координаты n, если линии кромки за одно движение резания не перекрывает ее по протяженности на поверхности детали. В данном случае движение кромки по линии координаты g (или n) называется простым движением резания, так как для формирования номинальной поверхности детали и выполнения второй функции инструмента-снятия припуска -1 достаточно изменение лишь одного параметра движения. Если есть необходимость существования "холостой подачи", то ее выполняет вспомогательное движение, которое схемой формообразования не учитывается и его следует отнести к так называемому транспортному движению инстру-мента. Та же поверхность детали может быть получена, если инструмент кроме движения резания имеет одну подачу. В этом случае номинальная поверхность
детали является сгибающей однопараметрического семейства поверхностей
резания.
Инструмент имеет две подачи, поминальная поверхность детали является
огибающей двухпараметрического семейства поверхностей резания; является
огибающей поверхностью системы семейств поверхностей резания,
построенных при наличии трех параметров семейств (трех подач), четырех
подач и т.д.
Для всех этих случаев форма режущей кромки может быть выбрана по трем вариантам: линия кромки лежит на номинальной поверхности детали, является касательной к номинальной поверхности; есть произвольная линия (выпуклая или вогнутая, ломаная), форма которой определяется по соображениям - облегчения удаления припуска, но она должна быть выбрана так, чтобы в процессе формообразования пересечение номинальной поверхности детали линией режущей кромки не произошло, т.е. в сечении любой плоскостью, проходящей через контактную точку 0, радиус кривизны линии от сечения указанной плоскостью номинальной поверхности детали ра должен быть больше радиуса кривизны линии от сечения той же плоскостью поверхности резания рц. Зная уравнения поверхности детали в системе ХоУо2о и уравнение поверхностей резания в той же системе, условие не подрезания тела детали можно записать в виде;
Рd > Рu
При задании формируемой номинальной поверхности детали алгебраическим или натуральным уравнениями Pd в сечении плоскостью ХОY находится из уравнения [ ]:
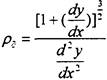
Для линии поверхности резания, представленной параметрическим уравнением рц в сечении той же плоскостью определяется из выражения:
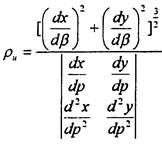
Кроме того, формообразование номинальной поверхности детали как огибающей семейства поверхности резания может быть осуществлено двумя способами. При последовательном выполнении движения - резания и подач и одновременном. Если в процессе формообразования одновременно изменяются
параметры движения резания и подач (одной или нескольких), то результирующее рабочее движение режущей кромки называют сложным движением резания. При последовательном выполнении движений кромка выполняет указанное выше простое движение резания при неизменности параметров подач, которые изменяются при осуществлении последующего движения формообразования в направлениях подач.
Для формообразования номинальной поверхности детали безразлично, какое движение резания осуществляет инструмент - простое или сложное. Но в то же время, формы поверхностей резания, образованные при простом и сложном, движении режущей кромки, будут несколько отличаться друг от друга и в соответствии о этим будут отличаться размеры срезаемых слоев припуска. Однако известно, что это отличие является практически незначительным и им обычно пренебрегают при расчетах схем резания. В работе [2] сделана численная оценка этого изменения, которая подтверждает его не существенность даже для оценки технической шероховатости поверхности, определяемой пересечением поверхностей резания.
Для формообразования произвольной номинальной поверхности безразлично, является ли траектория точек контакта о номинальной поверхностью ее образующей или простей криволинейной координатной линией g (или n), так как в том и другом случае должно существовать движение, определяющее формирование соседнего семейства поверхностей резания по второй криволинейной координатной линии п. Единственным отличиям этих вариантов формообразования является лишь то, что в первом случае движение формообразования будет непрерывным, и во-втором прерывным последовательным, т.е. необходимо обратно-поступательное движение инструмента и последовательное выполнение подачи по линии координаты.
Из изложенного следует, что для универсального математического моделирования различных процессов формообразования поверхностей инструментами необходимо и достаточно рассмотреть процесс формирования произвольной поверхности детали на базе универсальной кинематической схемы. Осуществить ориентацию детали так, чтобы обрабатываемая поверхность имела контакт с режущей кромкой произвольной формы в общей точке 0 двух систем координат ХоYоZо и X2Y2Z2 (рис. 7). Формируемую поверхность считать заданной двумя линиями криволинейных координат g n п или ее образующей. Рассматривать произвольную номинальную поверхность детали следует как огибающую семейств огибаемых произвольных поверхностей резания. Так как погрешность, связанная с заменой сложного результирующего движения резания и формообразования на составляющие незначительна, то любое элементарное движение, указанное на универсальной кинематической схеме может быть выбрано за абсолютное движение резания. Перемещения, необходимые для формообразования произвольной поверхности детали, определяются временем последовательного контакта, режущей кромки с теоретически заданной поверхностью детали при ее огибании, поэтому безразлично в какой последовательности режущей кромкой могут быть выполнены перемещения в направлении всех движений универсальной схемы. Так как при сложном результирующим движении все перемещения режущей кромки выполняются одновременно, то необходимо установить связь между величинами перемещений и длительности цикла формообразования по
времени. Временем (т) может быть величина определяющая последовательный выход и вход режущей кромки или кромок в контакт о теоретической формируемой поверхностью при образовании последовательно: пары
18
формообразующих поверхностей резания в одном из семейств поверхностей и пары соседних семейств.
Согласно свойства вращательных и поступательных движений твердого тела, уравнение перемещений любой точки тела является общим законом движения в пространстве. Поэтому для вывода уравнения произвольных поверхностей резания необходимо и достаточно записать закон перемещения контактной точки О, прилежащей произвольной линии режущей кромки, при выполнении ею всех движений универсальной кинематической схемы последовательно. Для анализа процесса формообразования поверхности при существовании сложного результирующего движения резания необходимо определить абсолютное движение резания и достаточно установить связь между величинами отдельных перемещений, если это движение неопределенно.
В универсальной кинематической схеме (рис 7) будем считать заданной произвольную номинальную поверхность двумя линиями ее образующей и направляющей. В исходной момент формообразования точка контакта двух систем Х2Y2Z2 и ХоYоZо принадлежит теоретически заданной поверхности детали. Для формообразования произвольной поверхности как огибающей
семейства огибаемых поверхностей резания достаточно, чтобы за время (т) точки О, принадлежащая режущей кромке, завершив движение по траектории резания снова стала принадлежать формируемой поверхности или любой из двух линий, например ее образующей.
Будем считать, что при существовании Zu режущих кромок инструментом является фреза, у которой точки всех кромок в сечении плоскостью Y202Х2 расположены через центральный угол ф=2п/Zu. Тогда за время т примем отрезок времени, соответствующий повороту системы инструмента X2Y2Z2 вокруг оси O2Z2 на центральный угол ф. Обозначим перемещения по направлениям движения, указанных на универсальной схеме,
за время т:
Поворот системы X2Y2Z2 по стрелке А на угол ф=2п/Zu
Поворот системы ХоYоZо по стрелке Б на угол Q=ф*п2/nu
Перенос начала системы координат X2Y2Z2 относительно осей
![]()
Где nu и пd - числа оборотов в минуту системы:
Х2Y2Z2 вокруг оси O2Z2 и ХоYоZо вокруг оси 02Х2 соответственно: Sг(х), Sг(у), Sz(2) - перемещения в расчете мм/зуб вдоль осей системы Х2У2Z2.
Общее уравнение поверхностей резания может быть представлено последовательной записью систем параметрических уравнений.
|
|
- параметрическое уравнение режущей кромки в контактном положении в системе координат инструмента
(1)
| 19 |
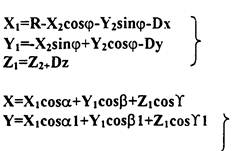
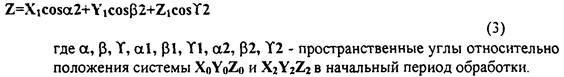
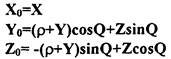
(5)
Таким образом, по уравнению (5) можно рассчитать координаты (ХоYoZо) точек поверхности или семейства поверхностей резания, относящиеся к исходной пространственной системе детали, в которой определенным образом ориентирована деталь и задана геометрически произвольная, формируемая поверхность. При расчете координат точек поверхностей резания на ЭВМ очевидна возможность определения множества точек, принадлежащих формируемой поверхности детали, простой проверкой условия удовлетворения рассчитываемых координат алгебраическому или натуральному уравнению поверхности детали, заданной произвольно в той же системе. Выполнение этого условия дважды будет означать двукратное касания линией режущей кромки теоретически заданной, формируемой поверхности детали. Так как движение кромки осуществляется от исходного контактного положения по траектории резания, то двойное выполнение упомянутого условия за полный цикл формообразования определит возможный способ механической обработки. Количество кинематических вариантов формообразования заданной поверхности выбранной линией режущей кромки предполагаемого инструмента будет зависеть от:
а) исходного положения систем координат детали и инструмента в начале цикла формообразования, характеризуемого контактом линии кромки с поверхностью детали в точке О, задаваемого выбором углов A, B, Y (при расчете шести оставшихся углов по уравнениям связи их косинусов);
б) сочетания действующих движений из числа существующих (nu, nd, Sх, Sу, Sz), определяющего результирующее движение резания, составляемое из попеременного включения пяти элементарных движений для каждого случая. При этом численная оценка множества общих точек поверхностей резания и детали, выполняемая за заданный, расчетный временной цикл формообразования будет определять производительность способа механической обработки. Выбор способа механической обработки и следовательно его производительность уже будет зависеть от комбинации, определяемых пунктами а) и б), а также от ...
в) существования (Ru=/0) и величины радиуса движения режущей кромки относительно центра си системы координат, предполагаемого инструмента (Х2,Y2,Z2); заданного выбираемой линией режущей кромки.
г) выбора главного движения резания, определяющего скорость резания (Vр), из числа существующих в комбинациях, определяемых пунктами а), б) в) при присвоении оставшимся, существующим движениям функции подач;
д) возможности увеличения скорости выбранного движения резания при многолезвийной обработке, соответствующей условию nu=/0, пu=f(Vp), определяющему фрезерование, при котором многолезвийная обработка характеризуется приближенно равной мощности резания с однолезвийной, т.е.
20
Шаг дискретного движения режущей кромки от скорости рсзания принимался равным:
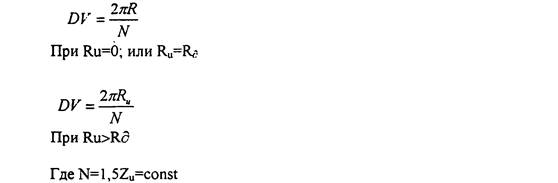
Zu - принятое произвольно число режущих кромок возможной фрезы
Шаг дискретного движения кромки в направлениях возможных подач принимался постоянным и равным
![]()
где S0=1мм=const, принятое значение подачи при получистовой обработки.
Это обеспечивало шаговое равенство расположения контактных точек (КТ) на формируемой поверхности при сравнении различных способов обработки из принципиально-возможных, что позволяло сравнить однотипные операции, обеспечивающие одинаковую технологическую шероховатость поверхности.
Печать алгоритма предусматривает выход характеристик способа механической обработки для трех наиболее эффективных, из принципиально возможных, сравниваемых по производительности.
22
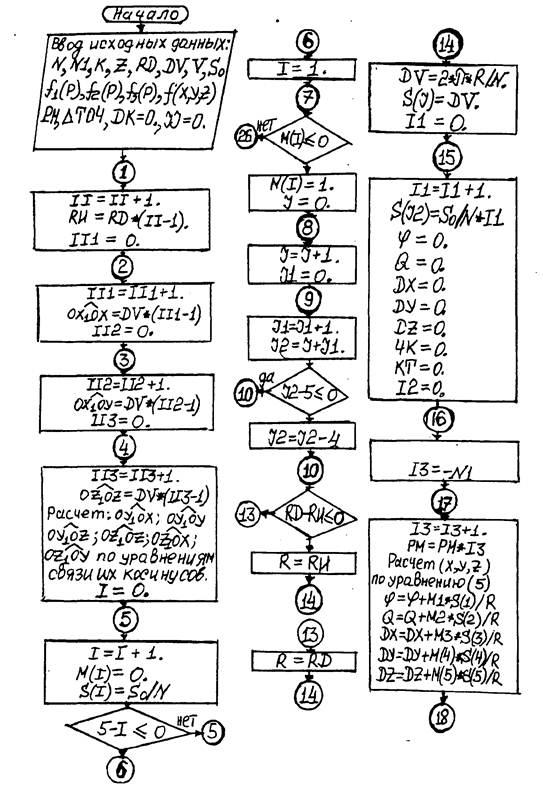
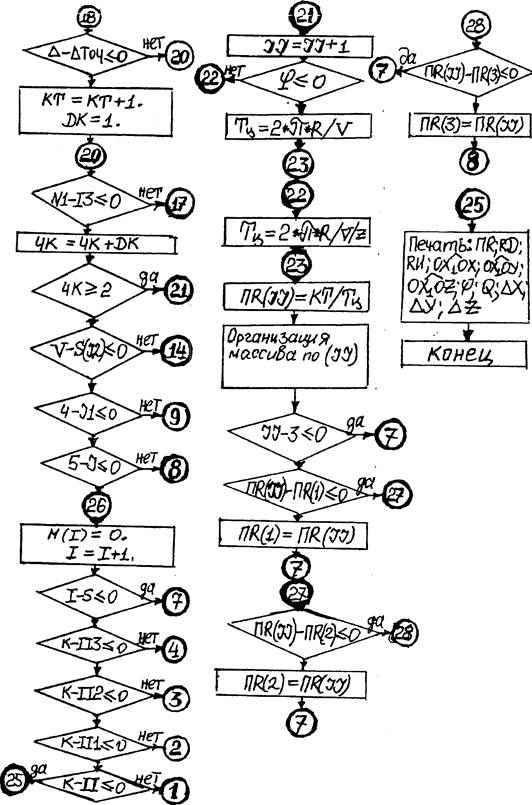
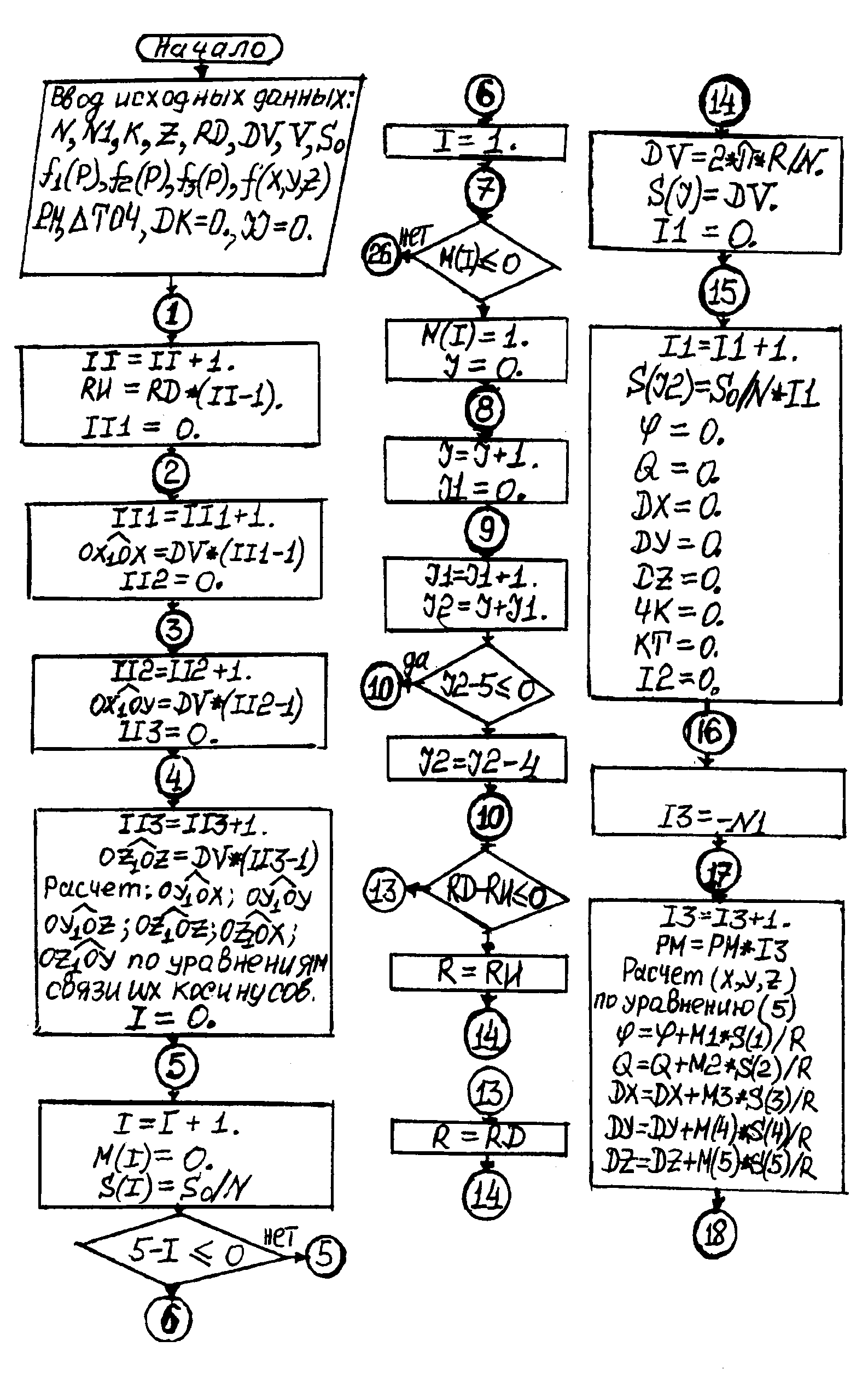
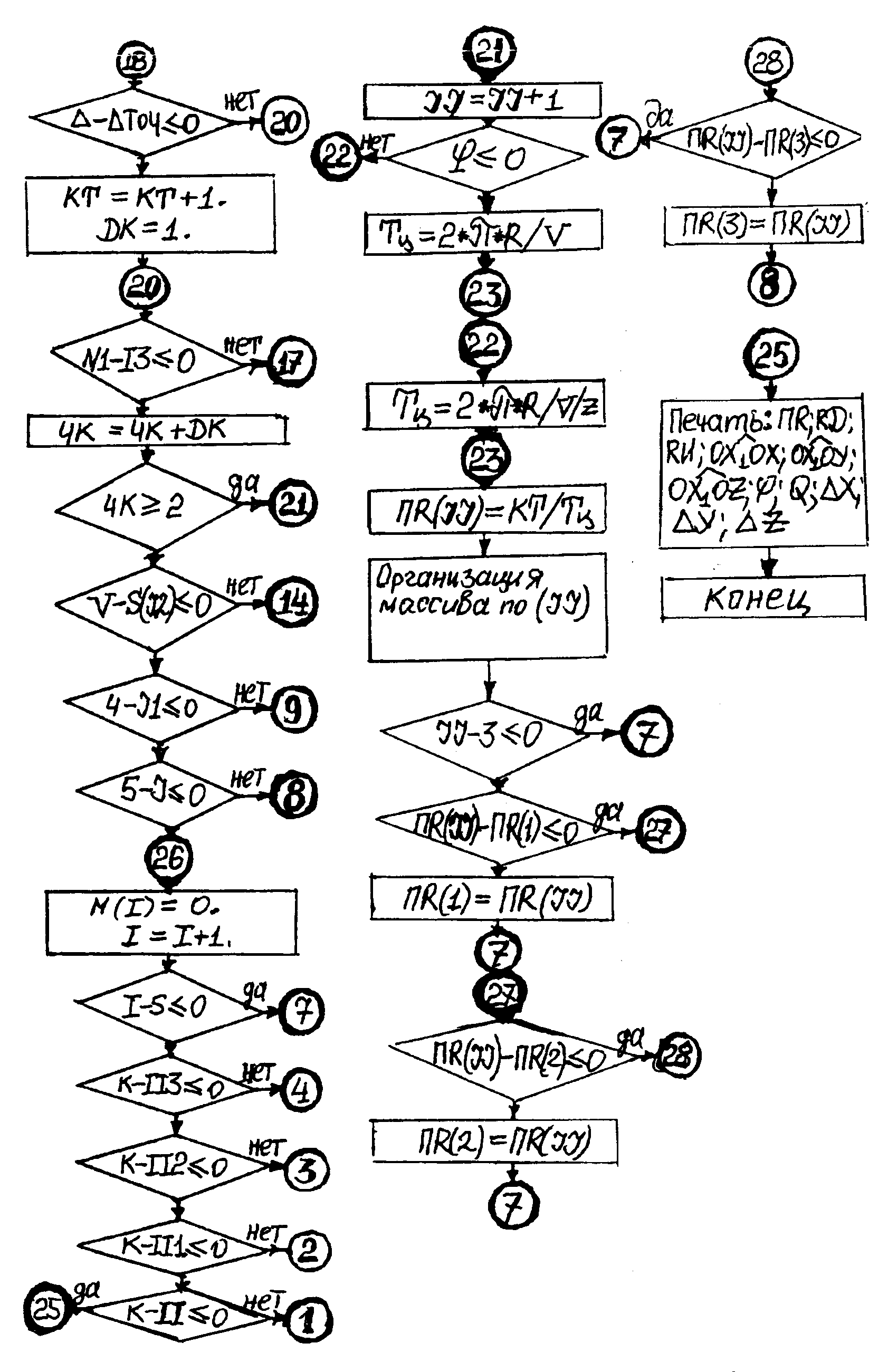
Блок-схема алгоритма поиска трех наиболее производительных схем формообразования заданной поверхности из принципиально возможных
Пример расчетного анализа на ЭВМ способов формообразования наружных поверхностей вращения деталей типа валов показал:
1) В случае формообразования точкой (из условия выбора кромки, как участка пересечения двух прямых линий, или существования малого радиуса К), наиболее эффективны три способа (рис. 8) а), б), В).
2) В случае формообразования прямой линией способы повторятся:
для случая а) Пр=45000 (кТ) для случая б) Пр= 10000 (кТ) для случая в) Пр=450000 (кТ)
3) В случае формообразования винтовой линией с углом подъема W=45° на радиусе фрезы R=2*Rc, получено три способа обработки на базе схемы - б);
а) оси фрезы и детали параллельны = 10000 (кТ)
б) находятся под углом скрещивания = 10000 (кТ)
в) находятся под углом скрещивания и фреза имеет ещё подачу вдоль своего вращения = 450000(кТ).
Таким образом, метод и алгоритм позволяют системно решить такую сложную задачу, как определение наиболее эффективных способов механической обработки из числа принципиально, - возможных. Алгоритм существенно облегчает работу в области повышения эффективности операций механической обработки, позволяет решить эту задачу на уровне изобретений.
Так схема обработке изображенная на фиг. в. Защищена была авторским свидетельством ещё в 1946 г. Схема б (1) составила предмет изобретения, а схемы 6(2) и 6(3) разработаны защищены авторскими свидетельствами при реализации описанного алгоритма на ЭВМ. Схема представленная на фиг. а известна как самая эффективная при формообразовании точкой.
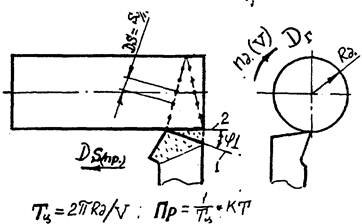
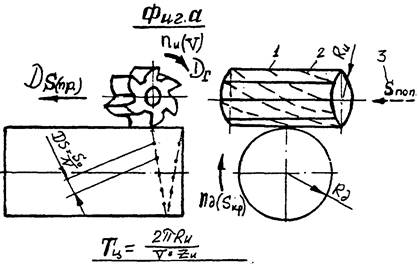
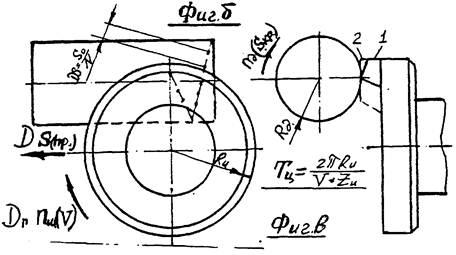
РИС. 8 Наиболее эффективные схемы обработки наружных поверхностей вращения.
26
Похожие работы
... из числа принципиально, - возможных. Алгоритм существенно облегчает работу в области повышения эффективности операций механической обработки, позволяет решить эту задачу на уровне изобретений. Определение наиболее эффективных способов механической обработки заданных поверхностей детали машин. Ранее нами был рассмотрен поисковый алгоритм определения схем формообразования заданных поверхностей и ...
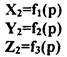
0 комментариев