КОСВЕННЫЕ ИЗМЕРЕНИЯ

2.7. КОСВЕННЫЕ ИЗМЕРЕНИЯ

При косвенных измерениях искомое значение величины находят расчетом на основе измерения других величин, связанных с измеряемой величиной известной зависимостью

Результатом косвенного измерения является оценка величины А, ко­торую находят подстановкой в формулу (2.18) оценок аргументов а_i.

Поскольку каждый из аргументов а, измеряется с некоторой погреш­ностью, то задача оценивания погрешности результата сводится к сум­мированию погрешностей измерения аргументов. Однако особенность косвенных измерений состоит в том, что вклад отдельных погрешностей измерения аргументов в погрешность результата зависит от вида функ­ции (2. 18).

Для оценки погрешностей существенно разделение косвенных изме­рений на линейные и нелинейные косвенные измерения. При линейных косвенных измерениях уравнение измерений имеет вид

где b_j— постоянные коэффициенты при аргументах а_i.

Любые другие функциональные зависимости (2.18) относятся к не­линейным косвенным измерениям.

Результат линейного косвенного измерения вычисляют по формуле (2.19), подставляя в нее измеренные значения аргументов.

Погрешности измерения аргументов могут быть заданы своими гра­ницами , либо доверительными границами , с доверительными вероятностями Р_i .

При малом числе аргументов (меньше пяти) простая оценка погреш­ности результата получается суммированием предельных погрешно­стей (без учета знака), т.е. подстановкой границ ... , в вы­ражение

(2.20)

Однако эта оценка является излишне завышенной, поскольку та­кое суммирование фактически означает, что погрешности измерения всех аргументов одновременно имеют максимальное значение и сов­падают по знаку. Вероятность такого совпадения практически равна нулю. Для нахождения более реалистичной оценки переходят к ста­тистическому суммированию погрешностей аргументов. Полагая, что в заданных границах погрешности аргументов распределены равномерно, доверительные границы (Р) погрешности результата измерения рассчитывают по формуле

(2.21)

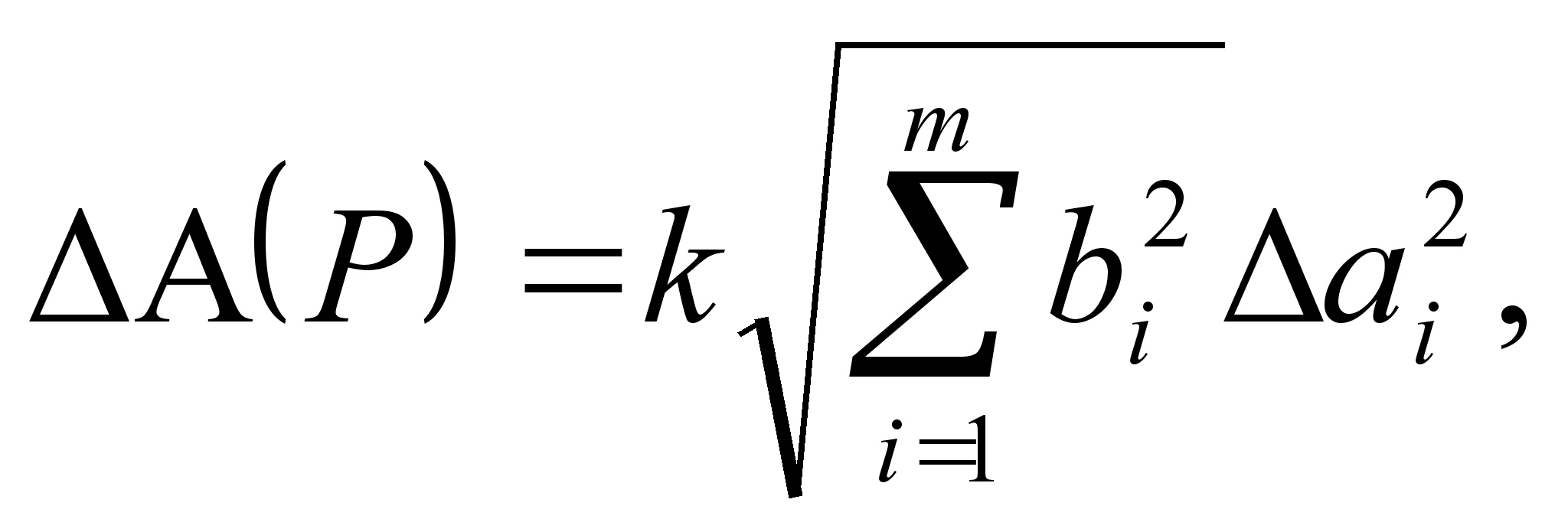
где коэффициент k определен в (2.15).

Если погрешности измерения аргументов заданы доверительны­ми границами с одинаковыми доверительными вероятностями, то полагая распределение этих погрешностей нормальным, доверитель­ные границы результата находят по формуле

(2.22)

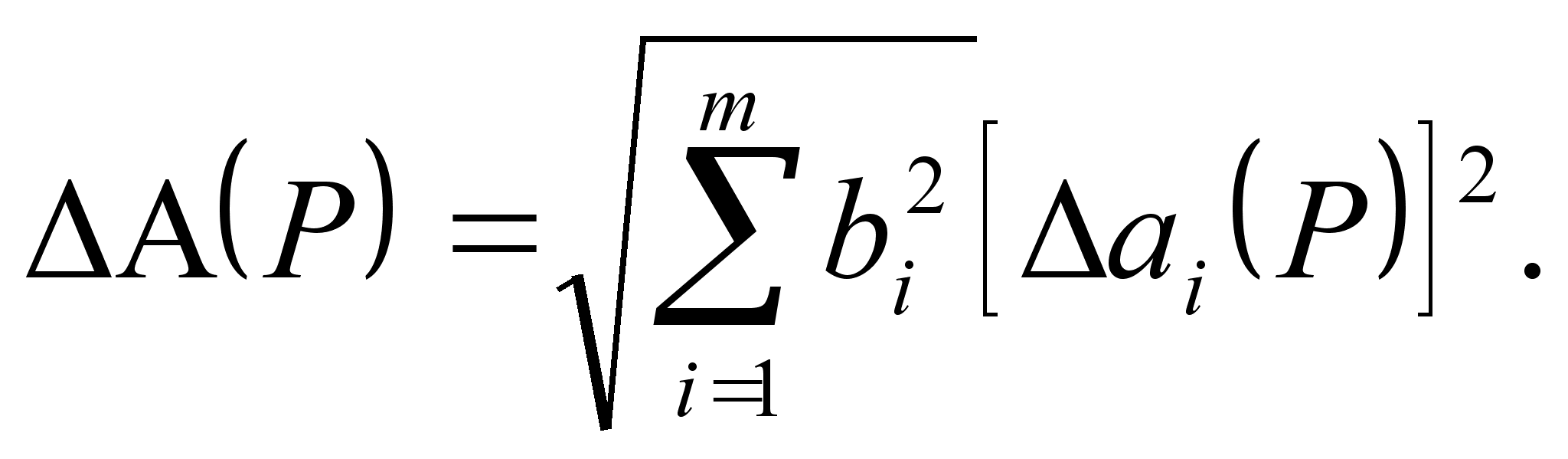
При различных доверительных вероятностях погрешностей аргумен­тов их необходимо привести к одному и тому же значению Р.

Нелинейные косвенные измерения характеризу­ются тем, что результаты измерений аргументов подвергаются функцио­нальным преобразованиям. Но, как показано в теории вероятностей, любые, даже простейшие функциональные преобразования случайных величин, приводят к изменению законов их распределения.

Пример. Результат измерения аргумента подчиняется нормальному распределению плотности вероятностей, кривая которого 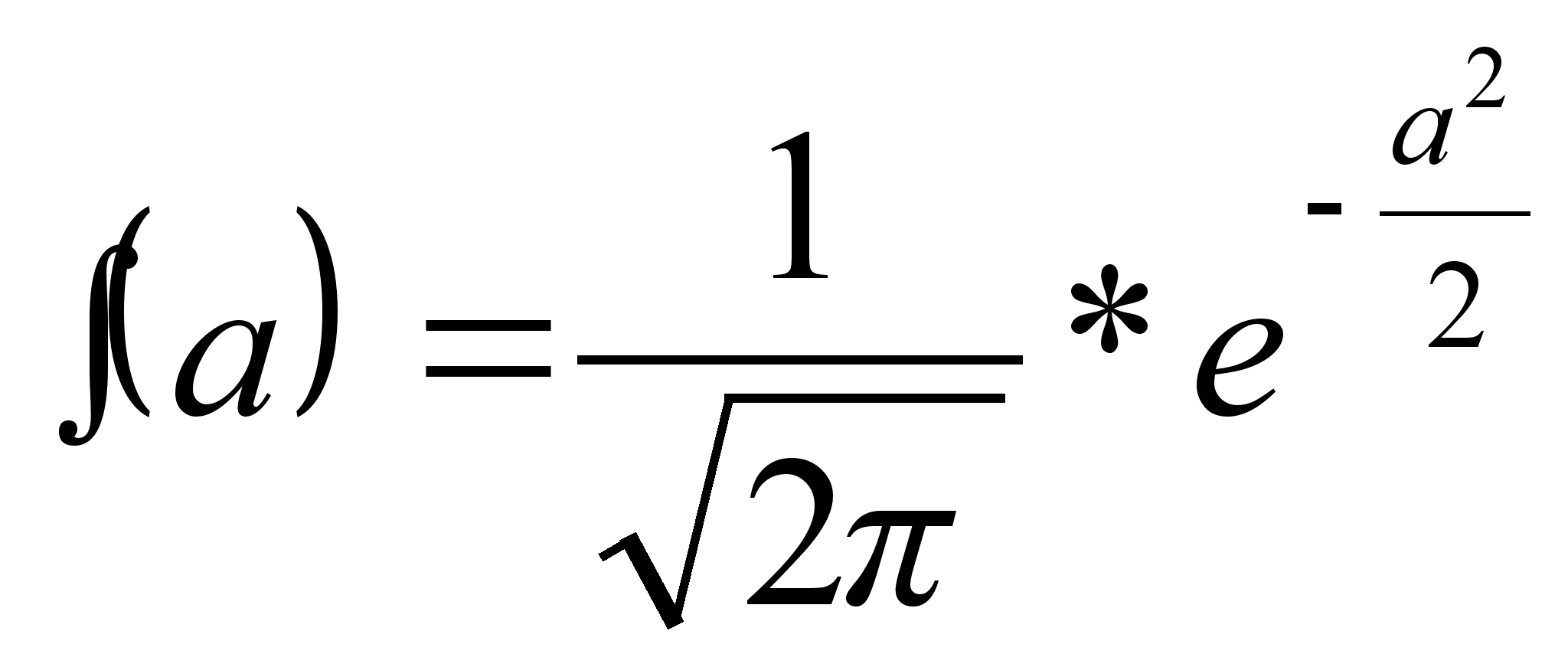показана на рис. 2.13, а.

При возведении измеренного значения величины в квадрат q = а² график плотности распределения претерпевает изменения и принимает вид, показанный на рис. 2.13, б (вы­вод формулы опускаем). Уравнение кривой в этом случае имеет следующий вид:

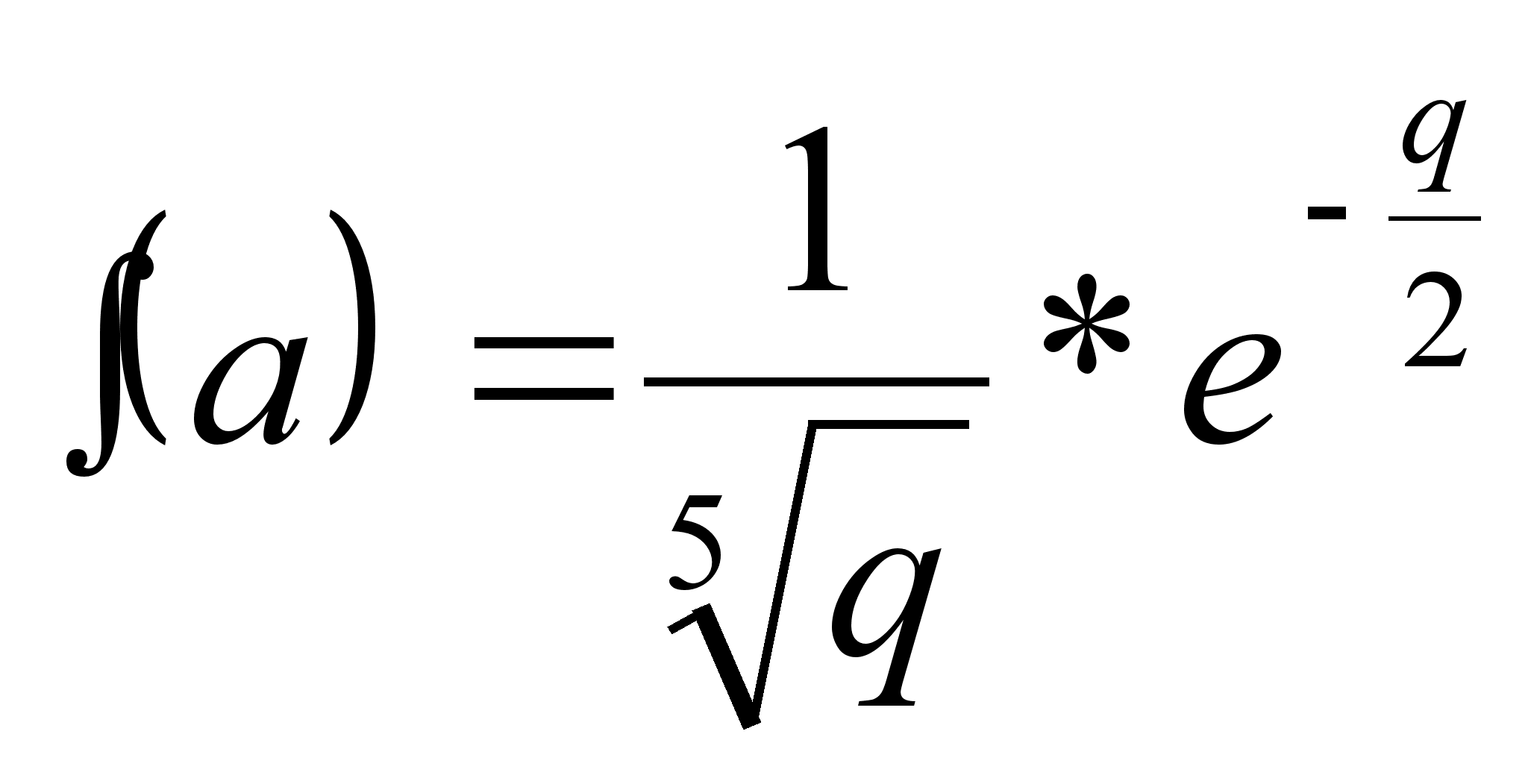
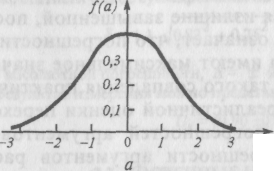
Рис. 2.13. Графики плотности распределения вероятности результата измерения, подчиняющегося нормальному закону, и квадрата этого результата измерения

При сложной функции (2.18) и в особенности если это функция не­скольких аргументов, отыскание закона распределения погрешности результата связано со значительными математическими трудностями. Поэтому при нелинейных косвенных измерениях приходится отказы­ваться от использования интервальных оценок погрешности результата, ограничиваясь приближенной верхней оценкой ее границ. В основе при­ближенного оценивания погрешности нелинейных косвенных измерений лежит линеаризация функции (2.18) и дальнейшая обработка результа­тов, как при линейных измерениях.

Запишем выражение для полного дифференциала функции А:

(2.23)

По определению полный дифференциал функции — это приращение функции, вызванное малыми приращениями ее аргументов.

Учитывая, что погрешности измерения аргументов всегда являются малыми величинами по сравнению с номинальными значениями аргу­ментов, можно заменить в (2.23) дифференциалы аргументов dа_i, на по­грешности измерений а_i, а дифференциал функции dA на погрешность результата измерения :

(2.24)

Полагая, как и прежде, что распределения погрешностей аргументов подчиняются равномерному закону, при числе слагаемых m < 5 грани­цы погрешности результата можно определить по формуле (2.20). В том случае, когда погрешности аргументов заданы их доверительными гра­ницами, оценку погрешности результата измерения вычисляют по (2.22). В обеих случаях роль коэффициентов b₁,b₂,…,b_m выполняют частные

производные

Применив формулу (2.24), получим несколько простых правил оце­нивания погрешности результата косвенного измерения.

Правило 1. Погрешности в суммах и разностях. Если a₁ и а₂ измерены с погрешностями и и измеренные значения использу­ются для вычисления суммы или разности А = а_1*а_2, то суммируются абсолютные погрешности (без учета знака):

Правило 2. Погрешности в произведениях и частных. Если из­меренные значения а₁, и а₂ используются для вычисления А = а_1* а₂ или А = а₁/а₂, то суммируются относительные погрешности , где .

Правило 3. Измеренная величина умножается на точное число.

Если а используется для вычисления произведения А = В * а, в котором В не имеет погрешности, то А = |В|а .

Правило 4. Возведение в степень. Если а используется для вычисления степени А = аⁿ, то А = .

Правило 5. Погрешность в произвольной функции одной пере­менной. Если а используется для вычисления функции А(а), то

Вывод этих правил не приводится и может быть легко сделан само­стоятельно. Использование правил позволяет получить не слишком завы­шенную оценку предельной погрешности результата нелинейного косвен­ного измерения при не слишком большом числе аргументов (m < 5).

Пример. Производится косвенное измерение электрической мощности, рассеиваемой на резисторе сопротивлением R при протекании по нему тока I. Так как Р =I²R, то, при­меняя правила 2 и 4, получим

Пример. Измерением найдено значение утла Необходимо найти cos. Наилучшая оценка для cos20° = 0,94. Погрешность должна быть выражена в радианах, т.е. = 3° = 0,05 рад. Тогда по правилу 5 (cos) = (sin20°)*0,05 = 0,34-0,05 = 0,02. Окончательно cos = 0,94±0,02 .

7.Преобразование измеряемой величины как косвенные измерения

При косвенных измерениях результат определяется на основании измерений величин, связанных с измеряемой величиной известной зависимостью. При этом в качестве примеров рассматривались случаи, когда закономерная зависимость выражалась строго математически. Однако строгая закономерность зависимости между величинами может быть неизвестна, хотя и известно, что такая зависимость существует. Например, известно, что электродвижущая сила термопары зависит от температуры. Определить эту зависимость на основании известных нам законов физики мы не можем даже для одной и той же пары металлов. На эту зависимостиь влияют малейшие отклонения в составах сплавов и технология их обработки. В этих случаях нужную нам зависимость мы можем определить методом совместных измерений. И не только определить, но и исследовать, и изучить постоянство и воспроизводимость этой зависимости влияния на нее внешних воздействий. Когда зависимость одной величины от другой будет нам хорошо известна, мы имеем возможность измерять нужную нам величину на основании измерений других величин, связанных с измеряемой известной зависимостью.

Описанные измерения следует также отнести к косвенным измерениям как одну из его разновидностей. Разновидностью косвенных измерений является также случай нахождения значения измеряемой величины путем прямых измерений компонентов известной формулы, определяющей ее зависимости от этих компонентов. Эта разновидность косвенных измерений относится к случаю нахождения значения измеряемой величины по ее зависимости от других величин, определяемой путем совместных измерений. Вторая разновидность косвенных измерений может рассматриваться так же, как измерение путем преобразования измеряемой величины в другую, по природе своей существенно отличающуюся от измеряемой, но связанную с ней устойчивой зависимостью.

Похожие работы

Регулювання метрологічної діяльності

Скачать

37376

0

0

... і оборони України регламентуються окремим положенням, яке затверджується Кабінетом Міністрів України за поданням Міністерства оборони України і ЦОВМ та не повинно суперечити цьому Закону. Особливості метрологічної діяльності у сфері наукових досліджень і розробок в Україні регламентуються окремим положенням, яке затверджується Кабінетом Міністрів України за поданням Національної академії наук ...

Шпаргалки по метрологии

Скачать

96282

0

40

... измерений на рабочем месте. Чтобы эти службы эффективно выполняли стоящие перед ними задачи необходимо научное, техническое и правовое обеспечение их деятельности. Научной основой МО является метрология - наука об измерениях. Техническую основу МО составляют: система государственных эталонов единиц ФВ; система передачи размеров единиц ФВ от эталонов всем средствам измерений с помощью образцовых ...

Державна метрологічна система

Скачать

22473

0

1

... , оформлення та розгляд матеріалів за результатами державних випробувань визначаються відповідним ДСТУ. Державна метрологічна атестація, повірка та калібрування засобів вимірювальної техніки Державна метрологічна атестація засобів вимірювальної техніки Засоби вимірювальної техніки, які не підлягають державним приймальним випробуванням і на які не поширюється державний метрологічний нагляд, ...

Основы стандартизации, метрологии и сертификации

Скачать

442965

6

19

... ГОСТ Р. Техническими регламентами II уровня являются: государственные и межгосударственные стандарты (далее — государственные стандарты), содержащие обязательные требования; правила по стандартизации, метрологии, сертификации; общероссийские классификаторы. Нормативные документы III уровня представлены стандартами, сфера применения которых ограничена, определенной отраслью народного хозяйства ...