Расчёт рабочего цикла двигателя внутреннего сгорания автотракторного типа с помощью персональной ЭВМ

Теория и методика решения задачи

Задача сформулирована в прямой постановке, когда известны основные данные двигателя (диаметр цилиндра, ход поршня, степень сжатия, тип камеры сгорания), а также вид топлива и требуется определить показатели его эффективности и экономичности. На основе разработанной физико-математической модели (ФММ) с помощью персональной ЭВМ получают:

расчётную индикаторную диаграмму двигателя, для этого рассчитываются
функции V(φ); m(φ); T(φ); P(φ);

цикловые показатели двигателя (индикаторную работу цикла Li, индикаторную мощность Ni);

удельные цикловые показатели (среднее индикаторное давление p_i; индикаторный КПД η_i; удельный индикаторный расход топлива g_i);

данные о влиянии определенного фактора Z (конструктивного, режимного, регулировочного, эксплуатационного и т.д.) на показатели двигателя и на состояние рабочего тела в цилиндре.

Решение поставленной задачи завершается общей оценкой технических качеств двигателя, а также принятием инженерного решения (или выдачей рекомендаций) о рациональном выборе конкретных конструктивных, регулировочных и других характеристик. Если последнее невозможно, то ограничиваются констатацией выявленного влияния фактора Z на конечные результаты и объяснением физических причин этого влияния.

Методы решения задачи

Задача решается с помощью физико-математической модели 2-го уровня, включающей дифференциальные и конечные уравнения для определения четырёх параметров состояния рабочего тела (объёма V, массы m, температуры T и давления P). При разработке модели приняты следующие допущения:

1) процессы газообмена (выпуска, продувки, впуска) не рассчитываются, так как они протекают при малых перепадах давлений и вносят незначительный энергетический вклад в сравнении с другими процессами; влияние этих процессов на показатели двигателя учитывают на основе статистических данных путём выбора
начальных условий;

2) теплоёмкости рабочего тела принимаются различными для свежего заряда и для продуктов сгорания, но неизменными для процесса сжатия, а также для процессов сгорания-расширения; указанные теплоёмкости выбраны средними в диапазоне температур и состава рабочего тела;

3) температуры ограничивающих стенок (поршня, крышки и цилиндра) считаются одинаковыми в течение цикла;

4) параметры рабочего тела являются неизменными по объёму в любой момент времени;

Система дифференциальных уравнений дополнена соотношениями, описывающими реальные процессы сгорания и теплообмена со стенками. Решается система уравнений на персональной ЭВМ методом Эйлера. Начальные условия (параметры рабочего тела в цилиндре в начале счёта-Va, ma, Ta, Pa) задают, пользуясь опытными статистическими данными, и уточняют с помощью уравнения состояния. Граничные условия (давление P_k и температура T_k на впуске, давление P_т и температура T_т на выпуске, температура T_w ограничивающих стенок) оценивают по экспериментальным материалам. Уравнения выражают зависимости параметров рабочего (V, m, T, P) и некоторых других характеристик (закономерностей сгорания и теплообмена) от угла поворота коленчатого вала φ. Начало отсчёта угла φ выбирают в начале такта впуска при положении поршня в ВМТ, поэтому рас-
чёт рабочего цикла ведут в диапазоне φ=180…450°. Шаг интегрирования выбирают в пределах ∆φ=1..5°.

Физико-математическая модель рабочего цикла

Основная система уравнений включает кинематические соотношения, характеризующие изменение объёма и поверхности цилиндра, уравнения материального и энергетического баланса, а также уравнения состояния рабочего тела.

Объём цилиндра изменяется в соответствии с закономерностями кривошипно-шатунного механизма (первое кинематическое уравнение):

, (1)

где Vc-объём камеры сжатия, м³;

Fп-площадь поршня, м²;

rk-радиус кривошипа, м;

λk-отношение радиуса кривошипа к длине шатуна.

Путём дифференцирования соотношения (1) получим приращение объёма:

(2)

которое представляет собой первое кинематическое уравнение в дифференциальной форме.

Так как процессы газообмена не рассматриваются, то масса рабочего тела в цилиндре изменяется только за счёт испарения и сгорания топлива. В дизельном двигателе топливо поступает в цилиндр в жидком виде, и в таком состоянии оно
рабочим телом не является. Затем топливо испаряется и сгорает, образуя газообразные продукты сгорания. Различие по времени между испарением и сгоранием в реальных условиях ДВС невелико, поэтому будем считать, что увеличение массы рабочего тела за счёт топлива происходит в процессе сгорания.

Следовательно, приращение массы рабочего тела можно представить в виде:

d_m=∆m_тцЧdx, (3)

где ∆m_тц - цикловая массовая подача топлива;

х-доля топлива, сгоревшего в цилиндре к данному моменту времени.

При отсутствии сгорания d_x=0 и d_m=0, то есть масса рабочего тела остаётся неизменной. Это наблюдается в процессах сжатия и расширения.

Соотношение (3) является уравнением материального баланса в цилиндре двигателя внутреннего сгорания.

Уравнение энергетического баланса в цилиндре составлено на основе первого начала термодинамики для закрытой нетеплоизолированной системы:

, (4)

где C_v - теплоёмкость рабочего тела при постоянном объёме;

dQ_c - элементарное количество теплоты, подведенное при сгорании;

dQ_w - элементарное количество теплоты, подведенное от стенок (отведенное в стенки);

К - показатель адиабат рабочего тела.

Система основных уравнений замыкается с помощью уравнения состояния рабочего тела, которое может быть использовано в дифференциальной форме:

, (5)

или в конечной:

pV=RmT, (6)

где R - газовая постоянная рабочего тела.

Система уравнений (1)-(6) позволяет рассчитать цикл ДВС, получить необходимые функции:V(φ), m(φ), T(φ), P(φ) и построить индикаторную диаграмму. Для этого дополняют соотношениями, описывающими закономерности сгорания и теплообмена.

Элементарное количество теплоты, подведенное к рабочему телу при сгорании:

dQ_c=H_uЧ∆m_тцЧdx, (7)

где H_u - действительная теплота сгорания топлива, зависящая от рода топлива и состава смеси (соотношения между количеством топлива и воздуха в смеси).

Величина H_u в свою очередь равна:

при α ≥ 1 H_u=H_uт

при α < 1 Hu=Huт-120Ч10⁶(1-α)Lo, (8)

где α - коэффициент избытка воздуха;

Huт - теоретическая теплота сгорания (при полном сгорании топлива);

Lo - теоретически необходимое мольное количество воздуха для сгорания 1 кг топлива.

Закономерность тепловыделения при сгорании описывается эмпирической формулой Вибе, полученной путем обработки многочисленных опытных индикаторных диаграмм многих двигателей:

(9)

где m₁ - эмпирический показатель сгорания, зависящий от типа двигателя (способа смесеобразования);

φ_с,φ_z - углы поворота вала двигателя, соответствующие началу и концу сгорания.

Коэффициент 6,908 в уравнении (9) получен при условии, что к концу сгорания доля сгоревшего топлива составляет 0,999. Расчёт функции х ведут в диапазо не φ_c≤ φ ≤ φ_z, в других случаях, когда φ < φ_с или φ > φ_z, принимают dx=0, что соответсвует отсутствию сгорания.

Элементарное количество теплоты, подведенное к рабочему телу за счёт теплообмена со стенками, выражается с помощью формулы Ньютона-Рихмана:

(10)

где α_w- коэффициент теплоотдачи;

F_w - поверхность теплоотдачи;

T_w - температура стенок;

ώ - угловая скорость вращения вала.

В течение рабочего цикла ДВС возможны соотношения Tw >< Т. Если Tw>Т, то dQw>0, это означает, что тепловой поток направлен от стенок к рабочему телу. Если Tw < Т, то dQw < 0, и тепловой поток направлен от рабочего тела в стенки.

В формуле (10) величина Tw представляет собой осреднённую температуру поверхностей. В случаях, когда температуры основных деталей (поршня, крышки, цилиндра, клапанов) сильно отличаются, учитывают локальные условия теплообмена и формулу записывают в виде:

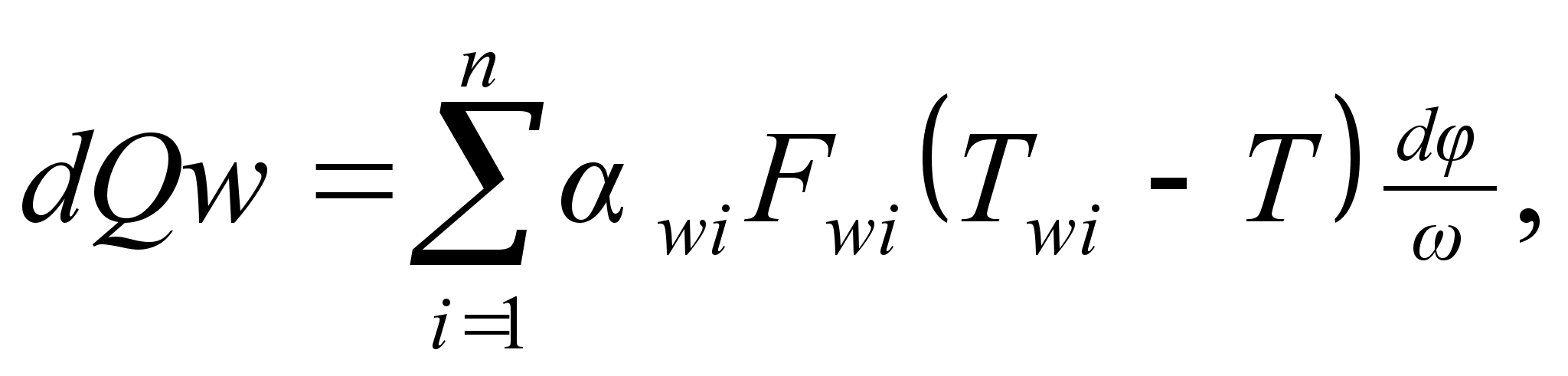(11)

где i - количество различных поверхностей теплообмена.

Площади поверхностей поршня и крышки зависят от их размеров и конфигурации и для данного двигателя постоянны, а площадь поверхности цилиндра является функцией угла поворота вала, что выражается вторым кинематическим уравнением:

, (12)

где D - диаметр поршня, м;

So - минимальное расстояние между поршнем и крышкой при положении поршня в ВМТ, м; во многих случаях величиной So можно пренебречь ввиду её малости.

Коэффициент теплоотдачи α_w зависит от условий теплообмена на границе газ-стенки, то есть от многих факторов. Его определяют по эмпирическим зависимостям. В данной методике использована эмпирическая формула Пфлаума:

, (13)

где α_w - коэффициент теплоотдачи, Вт/(м²ЧК);

Pк - давление наддува;

Pо - атмосферное давление.

При отсутствии наддува считают Pк = Ро.

Конечной целью расчёта является определение мощностных и экономических показателей двигателя. К мощностным показателям относятся:

индикаторная работа цикла

Li = ∫pЧdV, (14)

среднее индикаторное давление

Pi = Li / Vh, (15)

где Vh - рабочий объём цилиндра, м³;

индикаторная мощность

Ni = LiЧn / τ, (16)

где n - частота вращения вала;

τ - коэффициент тактности (для четырёхтактных ДВС τ=2).

По формуле (16) определяется мощность в одном цилиндре.

В качестве экономических показателей служат:

индикаторный КПД

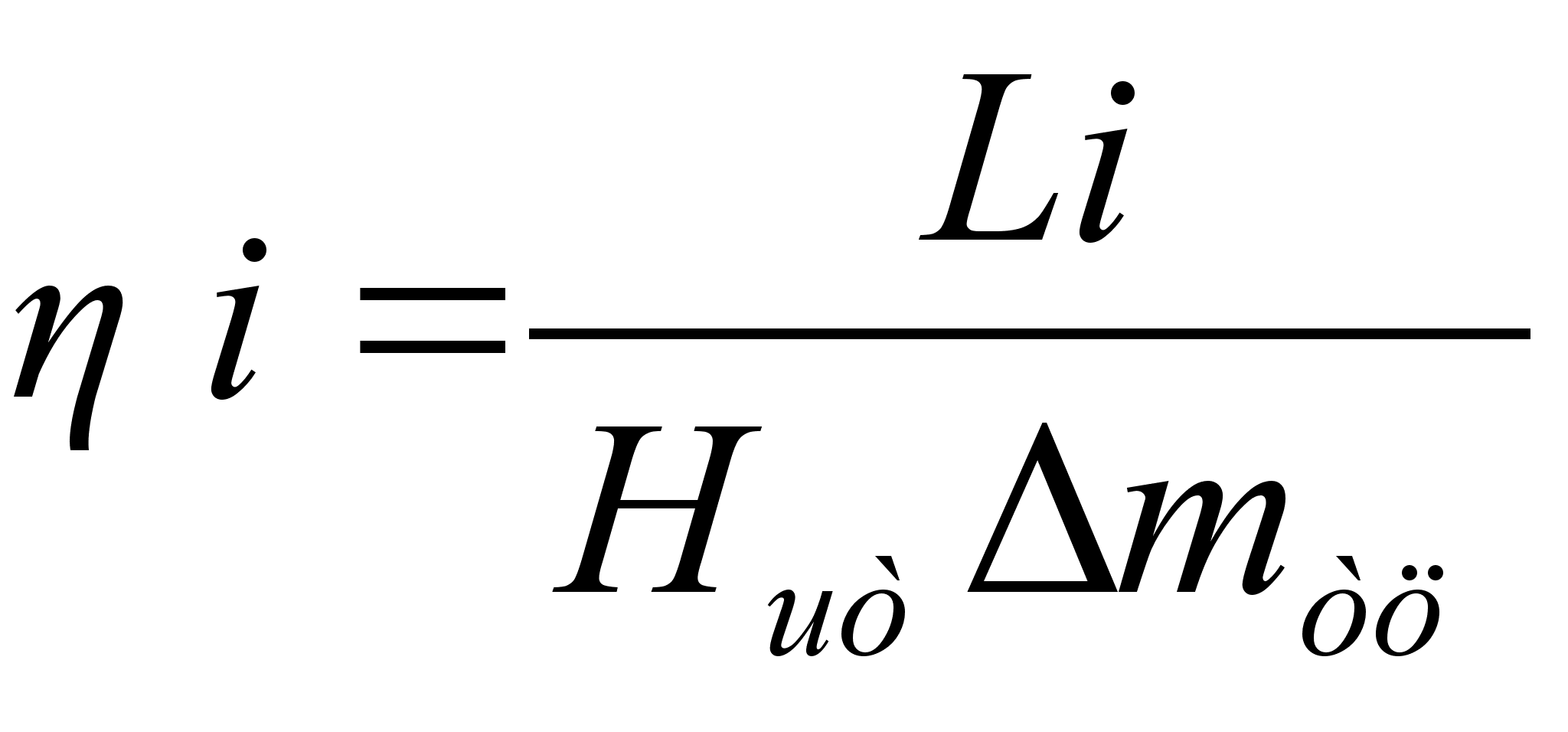, (17)

удельный индикаторный расход топлива, кг/(кВтЧч)

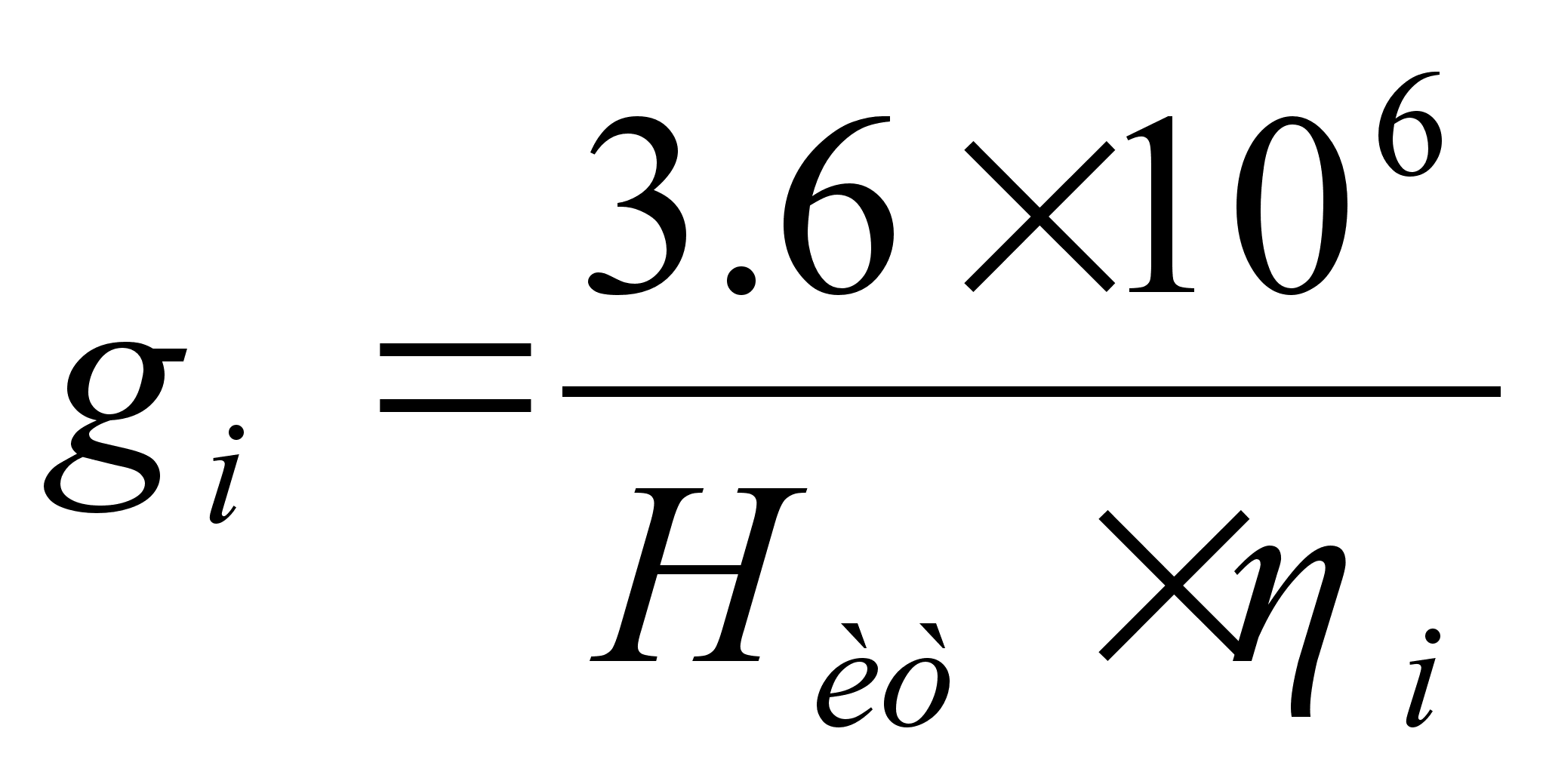, (18)

Эффективные показатели двигателя определяют, используя механический КПД η_m, который оценивают по статистическим данным:

Pe = PiЧ η_m, Ne = NiЧ η_m,

η_e = η_iЧη_m, g_e = g_i / η_m.

Систему уравнений, приведенную в данном разделе, решают численными методами с помощью ЭВМ. Для этого составляют алгоритм и программу расчётов.

Список литературы

1. Методические указания к курсовой работе “Расчёт рабочего цикла двигателя внутреннего сгорания автотракторного типа с помощью персональной ЭВМ”
/ Сост. Я.А. Егоров. Запорожье: ЗМИ, 1992.−31с.

2. Колчин А.И., Демидов В.П. Расчёт автомобильных и тракторных двигателей.−
М.: Высш. шк., 1980.−400с.