Навигация
100 Задач по Физике со вступительных экзаменов
задач
По
Физике
Динамика, кинематика, законы сохранения, механические колебания Гидростатика, идеальный газ тепловые явления Электростатика,электрический ток, магнетизм Оптика, квантовая физика, Атомное ядро 100 и 1 задача со вступительных экзаменов.Динамика
1) Кинематика
2) Законы сохранения
3) Механические колебания
45
Чаша в форме полусферы, радиусом R= 0,8 м вращается с постоянной угловой скоростью вокруг вертикальной оси. Вместе с чашей вращается шарик, находящийся на её внутренней поверхности. Расстояние от шарика до нижней точки чаши равно её радиусу. Определите угловую скорость W вращения чаши?
Решение: Шарик вращается по окружности радиуса r 2r=R; r=0,4 м
ma = F + mg + N; x: o= N sin30 – mg; y: ma= N cos30
(1) : N= mg / sin30 =2mg a= W R
ma = 2mg cos30 ----- W R = 2g cos30; W = (2g cos30 / R)ПОД КОРНЕМ;
W*W = 2gcos30 / R; W = (20*3/2 / 0.4)под корнем =6..5 ( из-за того, что в равностороннем треугольнике является медианой
Ответ : W= 6,5 рад.К
47
Аэростат массой М=1,7 т равномерно опускается вниз. Определите массу баласта, который надо сбросить с аэростата, чтобы он стал равномерно подниматься вверх с той же скоростью. На аэростат действует Архимедова сила Fa =15 кН.
Решение: Сделаем рисунок, обозначим силы и спроецируем их . Получим систему:
Mg=Fс + Fа (M+m)g=2Fа (M+m)=2Fа/g
Mg=Fа – Fс (сложим) M-m=dm отсюда m=M-dm ; M+m=2M-dm следовательно dm=2M-(M+m); dm= 2M-2Fа/g
dm=3400-3000=400 кг.
Ответ: dm=400кг.
48
Несколько ледяных горок имеют одинаковую высоту R , но различный угол a наклона к горизонту. Как зависит время t скатывания санок с горки от её наклона ?
Получите зависимость t=f( a ), представьте её в виде графика ( достаточно показать общий вид кривой в границах изменения a и t ; трением пренебречь.
Решение: Чем меньше a , тем больше время скатывания.
Второй закон Ньютона : ma = N+ mg
X: N=mgcosa
Y: ma= mgsina a=gsina
Vо=0 S=at/2 sina=h/S S= h/sina
H/sina=gsinat / 2 ; tgsina=2R ; t= (2R / gsina) под корнем
Ответ: t= ( 2R / gsina )под корнем
49
Брусок равномерно скользит вниз по доске, имеющей наклон a =30 граад к горизонтальной плоскости. За какое время брусок соскользнёт с доски , если наклонить её под углом b =60 град. Доска L= 2м.
Решение: a=0; a= FiEi / m ; ma= N+ mg+ Fтр; 0=N-mgcosa Fтр=mgsina ; kmgcosa=mgsina k=tga k=tg30=1/ 3
ma=N+mg+Fтр
x: ma=mgsin60- kN
y: 0=N-mgcos60 N=mgcos60 ; a=gsin60-kgcos60
Vо=0; t= ( 2S / a)под корнем
t= ( 2L / (gsin60-kgcos60))под корнем t= (4м / 10м/с( 0,86-0,28))под корнем;
T= 0.83c
Ответ: t=0.83c
50
Санки массой m= 40 кг Тянут за верёвку по горизонтальной доске. Коэффициент трения между полозьями санок и дорогой К=0,05. Сила натяжения верёвки F = 150Н, направлена под углом b =30 град к горизонту. Определите ускорение санок.
Решение: 2-й закон Ньютона: ma=T+N+Fтр+mg
X: ma=Tcos30-Fтр;
Y: 0=Tsin+N-mg
..a=T(cos30+ksin30) / m – kg; Fтр=k(mg-Tsina)
a=150H(0.86+0.025 ) / 40 – 0.5 =2.8 м/с
Ответ: a=2.8м/с
51
Через неподвижный блок перекинута нить , к концам которой подвешены два груза. М=0,2 кг каждый. Трение в блоке отсутствует. На один из грузов положили перегрузок массой м = 0,01 кг ( 100г).
С какой силой перегрузок действует на груз во время движения ?
Решение Ia1I =Ia2I=IaI ; IT1I=IT2I=ITI – так как нить невесома и нерастяжима
2- ой закон Ньютона : Ma= T – Mg (1);; a= ma / 2M + m;
(M +m) a = (M + m)g -T ) сложим
ma= mg – N; N = m(g – a) след-но N=m(g – mg / (2M+ m)
IPI = INI ; N= 0,01 ( 10 –( 0,01 10) : (0,4 + 0,01) ) = 0,097 H
Ответ N = 0,097Н = 97 10 Н.
52
Вверх по дороге, имеющей угол наклона a =30 град к горизонту, движется со скоростью V = 54 км\час автомобиль. На каком минимально возможном расстоянии от перекрёстка необходимо начать торможение при красном сигнале светофора ?
Решение : ma = N + Fтр + mg ; X : ma = Fтр+ mg sin 30; Y: 0= N – mg
cos30; N= mg cos30;
ma= K N + mg sin30; ma= K cos30 + mg sin30; a = K g cos30 + g sin30;
Vo= 54 км\час= 15 м\с S = Vo : 2a; S= (Vo*Vо : 2g( K cos30 + sin30)
S= 225 : 20(0,085 +0,5)= 225: 11,7= 19,2 м
Ответ : S тормозной = 19,2 м
53
Горнолыжник массой м=80 кг скользит со склона горы, не отталкиваясь палками. Угол наклона горы a =50 град, К=0,1 ( коэффициент трения). Какую максимальную скорость может развить на спуске лыжник, если сила сопротивления воздуха пропорциональна квадрату скорости : Fс = с V ? Постоянная величина с= 0,7 м.\м, sin50= 0,77; cos50=0,64.
Решение: ma=Fс+Fтр+N+mg
В этот момент , когда скорость max a=0
X: 0= Fс+Fтр-mgsin50 (1)
Y: 0=N-mgcos50 N=mgcos50 (2)
CV=mgsin50-mgcos50k
V= ( mg(sin50-cos50k) / c) под корнем;
Vmax= ( 80*10(0.77-0.064) / 0.7) под корнем; = 2804 м/с
Ответ: Vmax=2804 м/с
54
Человек на вытянутой руке вращает в вертикальной плоскости ведро с водой. Какова должна быть минимальная частота вращения, чтобы вода из ведёрка не вылилась? Длина руки L= 53 см.
Решение; mg + N = ma; a = a = V : L; В момент отрыва воды от дна ведёрка N=0 , поэтому
V
mg =m – ; V= ( gL) под корнем; ; V=2,35
L
V = 2ПLn; (gL) под корнем; = 2ПLn ; n min = ( gL) под корнем;
/ 2ПL; n =2,35 / 3,45 = 0,7Гц
Ответ n =0,7 Гц
55
Космический корабль массой м=500 т начинает подниматься вертикально вверх. Сила тяги его двигателей F=20МН.
Определите вес находящегося в корабле космонавта. Если вес космонавта на Земле равен Ро=600Н.?
Решение: Fт-сила нат-я двиг-й
F-сила притяжения
F=GMm / r r=R
F=GMm / R
2-й закон Ньютона: Fт-F=ma; a=F/m- GM/R= F/m-g
a=20*10000000H / 5*100000 – 10= 40-10=30м/с
запишем для человека:
N-F=ma ; |P|=|N| N=ma+gMm / R
N=m(a+g): mg=600 m=60
P=60(30+10)=2400H=2.4 kH
Ответ: 2.4 kH.
56
Луна вращается вокруг Земли по круговой орбите радиусом r=380000 км. Определите скорость движения Луны и период её обращения вокруг Земли. Считать известным: радиус Земли R=6400 км и ускорение свободного падения на её поверхности g=9,8 м\с .
Решение:На луну действует сила тяготения со стороны Земли. F=GMm / r
2-й закон ma=GMm / r r- растояние от Земли до Луны.
….a=GMR R / R*R*r*r=gR*R/*r*r V*V=ar=gR*R/r; V=R (g/r)под корнем; V=6400*0.005=33 kм/ч
T=2Пr/V ; T= 2.*3.14*380000 / 33=72315c ; T=1205мин ж T=20ч
Ответ: V=зз м/c; T=20ч
57
Спутник вращается по круговой орбите вблизи планеты, которую можно принять за однородный шар плотностью b.
Определите период вращения спутника Т -?
Решение : R=R+h
m=4/3ПRr T=2ПR/V
V1= ( gR) под корнем;
g=Gm/R V1= ( Gm/R) под корнем = (G4/3ПRr / R) под корнем = (4/3GПRr) под корнем;
T=6.28*100000 / 1.67r след-но T=3.8*100000 / r
Ответ: T=3.8*100000 / r
24
Лифт поднимается вверх с ускорением а= 2,2 м\с . в некоторый момент с потолка кабины начал падать болт. Чему равно время его падения на пол ? Н= 250 см ( высота кабины).
Решение Vo= 0 ( начальная скорость болта) ; S= at \ 2; a= g + a1;
t= (2S \ (g + a1)) под корнем ; t= ( 5m\ 12 m/c) под корнем =0.6 с
Ответ t= 0.6 с
81
Лодка с двумя пассажирами равномерно плывёт по озеру со скоростью V1 = 2 м\с. Один человек прыгнул с кормы лодки так, что его скорость относительно воды оказалась равной нулю. Затем аналогичный прыжок совершил 2-ой человек ( и его скорость относительно воды оказалась равной 0 ). С какой скоростью V2 стала двигаться лодка, если её масса в 2 раза больше массы каждого пассажира.
Решение: М- масса лодки, м- масса человека. Скорости людей равны скорости лодки в тот момент, когда они прыгают. Это следует из закона сложения скоростей.
Закон сохранения импульса (М + 2м) V1 =(М + м) И ; М= 2м; (2М = м) V1 = (М = м) И;
(М = 2м) 4м 4
И=------------- V1 ; И=------ V1 = --V1= 8\3 м\c;
( М = м ) 3м 3
Далее также применяем закон сохранения импулься (М + м) u = Мu1;
U1= (M+m)u/M ; u1= 3\2u;
И1 = 1\3 * 3\2 = 4 м\с
Ответ 4 м\с
82
Ракета , масса которой без заряда М= 600 г, при сгорании м=80 г пороха взлетает на высоту h= 180 м. Определите скорость выхода из ракеты пороховых газов. Считать, что порох сгорает на старте мгновенно .
Решение: В конце полёта ракета обладает потенциальной энергией Еп= MgR ;
En = 0,6 10 180= 1080H;
В начале полёта – кинетической Ек = MV \ 2; Из закона сохранения энергии следует Еп=Ек
MV
Mgh =------ ; V = 2gh = 60 м\с
2
Далее из закона сохранения импульса : mu = MV ; u= (MV/m под корнем)=0.6m1*60м/с / 0.08кг.=450м/с.
Ответ 450 м\с
83
Неподвижная молекула распадается на два атома. Масса одного из атомов в три раза больше, чем другого.
Определите кинетическую энергию каждого атома, если их общая энергия равна Е=0,032 Пдж
m1 V2
Решение Запишем закон сохранения импульса: m1V1 = m2V2; --- = --- = 3 ; V2= 3V1;
m2 V1
m1V1 m2V2 En1 m1V1 3m2V1
En1 + En2 = E; En1 =-------- ; En2= --------- ; ------ = --------- = ------------ = 1\3; 3En1 = En2;
2 2 En2 m2V2 m2 g V1
En1= 0,008Пдж Еn2 = 0,024 Пдж
Ответ : 0.008 Пдж; 0.024Пдж.
84
Верёвка длиной L= 4м и массой м=0,5 кг свешивается вертикально с края крыши. Какую работу необходимо совершить, чтобы поднять верёвку на крышу?
Решение Закон сохранения энергии А= En = En2 –En1; Центр тяжести верёвки – в центре верёвки.
En1 = 0 ( в центре выберем нулевой уровень); Ln2 = 2 м ( во втором положении от центра тяжести до крыши) ;
A= mgh = 0/5* 10* 2 = 10 Дж;
Ответ: 10 Дж
85
Хоккейная шайба, имея начальную скорость Vo= 36 км\ч, проскользила по льду до полной остановки путь S= 30м. Определите коэффициент трения k шайбы о лёд. Какая работа совершена силой трения за время движения шайбы? Масса шайбы м=200 г.
V - V0 V0 V0
Решение S= ---------- ; S= ---- ; a= ------- ; a= 5\3 = 1,66;
2a 2a 2S
2-ой закон Ньютона : ma= Fm = kmg; a=kg; k=a\g = 0,17;
A= Fтр*S = kmgS= 0,17 *0,2 *10 *30 = 10,2 Дж
2-ой способ: Eк1=mV/2 ; Eк2= 0 ( закон сохранения энергии) A= Eк1; A= mV/2= = 10 Дж
2
Ответ: k=0,17; A= 10ДЖ;
86
Конькобежец массой М=50 кг бросает горизонтально шайбу массой м=200 г со скоростью V=20 м\с.
На какое расстояние откатится конькобежец после броска шайбы? Коэффициент трения коньков о лёд k=0,02.
Решение: Закон сохранения импульса Mu=mV u=0.2*20/50=0.08м/с
u--- начальная скорость конькобежца
2-й закон Ньютона: Ma=Fтр ; a=kg=0.02*10=0.2 м/с*с
S=uu /2a = 0.0064/0.4=0.016 м
2-й способ. Закон сохранения.
Eк=Muu/2 ; A=FS S=A/F ; Fтр=kMg ; A=dEк=Eк ;
S=Muu/2kmg S=uu/2kg
S=0.016м
Ответ: S=0.016м
87
между двумя телами массой м1 и м2 находится сжатая пружина. Если тело массой м2 удерживать на месте, а другое освободить, то оно отлетит сос коростью V0. С какой скоростью будет двигаться тело массой м2 , если оба тела освободить одновременно ? Деформация пружины в том и другом случаях одинакова.
Решение: Закон сохранения энергии.: Ек=kxx/2 Eк1=m1VV/2
Eк=kxx/2 Eк1=m1V1V1/2 + Eк2 =m2V2/2
Запишем з-н с-ия импульса для этой системы: m1V1=m2V2 ; V1=m2V2/m1
M1VV=m1m2m2V2V2 /m1m1 + m2V2V2 ; m1V0V0=m2V2V2(m2/m1 + 1)
V2V2=m1m1V0V0 / m2(m2+m1) ; V2=(m1Vо 1 / m(m2+m1)) под корнем ;
Ответ: V2=m1Vо( 1/(m2(m2+m1)) под корнем;
88
Пуля массой м=10 г, летевшая горизонтально со скоростью V= 700 м\с, попадает в висщий на шнуре ящик с песком массой М=5 кг и застревает в нём. На какую высоту h, отклонившись после удара, поднимется ящик?
Решение: Закон сохранения импульса.
Vm=(M+m)U ; u=Vm/ (m+M)
Eк=(M+m)uu/2 ; Eк=0
Eк=0 ; Eк=(M+m)gR
Из закона сохранения энергии вытекает: Eк=En
(M+m)gh ; h=uu/2g; h=(Vm/(m+M)) / 2g=700*0.01 / 5.01*20=1095/20=0.97м
Ответ: h=0.1м
95
Подвешенный на пружине груз совершает вертикальные колебания. Когда груз имел массу m1 , период колебаний был Т=0,8с,а когда его масса m2, Т=0,6с.
Каким окажется период колебаний груза, если его масса равна (m1+m2) ?
Решение: Период колебаний пружины маятника T=2П ( m/k под корнем; )
T1=2П ( m1/k) под корнем; T1*T1=4П m1/k
…m1=kT1*T1/4П*П ; m2=kT2*T2/4П*П
m1+m2=k(T1*T1+T2*T2)/4П*П T1*T1+T2*T2=4П*П(m1+m2)/k ; T1+T2=
2П ( (m1+m2)/k) под корнем;
T= ( T1+T2) под корнем; T=1c
Ответ: T=1c
96
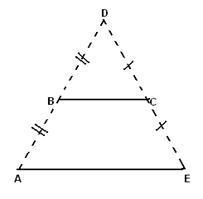
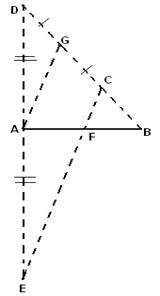
Период колебания математического маятника составляет T=2с, кокова будет Еп груза, если нить маятника отклонить на угол b=60 от вертикали? …m=0.01кг.
Решение: T=2П (L/g) под корнем; T*T=4П*ПL/g ; L=T*Tg/4П*П L=1
Т.к треугольник АВС – равносторонний : АВ=ВС=АС
СN- высота след-но CN-медиана BN=NA= 1/2L
NA=h=T*Tg/8П*П ; Eк=mgT*Tg/8П*П=0.01*100*4/78.8=0.05дж.
Ответ: Eп=0,05дж.
97
Ракета стартанула вертикально, первые h=500м поднимается с а=20м/сс
Затем до высоты h=1км, она двиг-ся с постоянной скоростью. Сколько полных колебаний совершит подвешенный в ракете маятник L=0,1м, за время когда ракета двигалась равномерно?
Решение: нач. скорость на 2-ом участке. V1=V2
S=V1*V1-Vо*Vо/2a ; V0=0; V1= 2as=141.4 м/с
S2=V0t; t=S2/V0=500м/141,4м/с=3,536с
Период колебаний математического маятника
T=2П (L/g) под корнем ; T=0.628c Ракета летит с постоянной скоростью а=0
Следовательно n=t/T=3.536/0.628=5.6 , n=5 ( полных)
Ответ: n=5
99
Вагон массой m=80т имеет пружинные рессоры, суммарная жёсткость которых
K=200кH/м. При какой скорости движения вагон начнёт сильно раскачиваться вследствии толчков на стыках рельсов? Длина рельсы L=12.8м
Решение:
T=2П ( m/k) под корнем ; V=L/T
V= L/2П (m/k) под корнем ; V=12.8 / 2*3.4*0.2 =10м/с
При этой скорости пройдет резонанс, т.е. совпадение наиб-х колебаний.
Ответ: V=10м/с
1.Гидростатика
2.Идеальный газ
3.Тепловые явления
16
Металлический стержень, к верхнему концу которого прикреплён пружинный динамометр, медленно погружают в цилиндрический сосуд с водой, имеющий площадь поперечного сечения S= 20 см куб. Определить, на сколько изменится показания динамометра, когда уровень воды в сосуде поднимется по сравнению с первоначальным на высоту h= 10 см.
Решение: при взвешивании в воздухе тела на него действуют Fт и Fнат; T1=mg
В воде: mg; T2; Fвыт;
-mg+T2+F=0 ; Fв=rgV=rgSh
T2=mg-Fв ; F=T1-T2=Fв=rgSh
F=1000кг/м* 10Н/м*20/10000м*0,1м=2Н
Ответ: 2Н
17
Резиновый мячик массой m и радиусом R погружают в воду, на глубину h и отпускают. На какую высоту, считая от поверхности воды. Выскочит мячик? Силы сопротивления при движении мяча в воде и воздухе не учитывать.
Решение: на шарик действуют Fа и mg
Fа=gVr=4/3ПRr
Ma=Fа+mg ; ma=Fа-mg ; a=Fа/m –g (силу сопрот-я воды не учит-м)
V=0; h=V*V/2a V= ( 2ah) под корнем;
V= ( 2(4/3m*g*П*R*R*R*r- g)h) под корнем;
Из закона сох-я:
MgH=mV*V/2 ; H=V*V/2g ;
Ответ: h=4/3*ПhR*R*R - h
18
В цилиндрический сосуд радиусом r =10 см налита вода. При этом сила давления воды на дно сосуда равна силе давления на его боковую поверхность. Каков уровень воды в сосуде?
Решение: Fд=pS. Где p=ghr ; S=ПR*R
Fб=(p)Sбок ; (p)=p/2—среднее давлениеводы на боковую поверхность:
Sбок=2ПRh
Fбок=gПRh*hr
По условию Fд=Fбок ; ghПR*Rr=rh*hgПR след-но h=R=0,1м
Ответ: h=0.1м
19
В дрейфующей льдине полярники проделали сквозное отверстие ( прорубь). Толщина льдины оказалась H= дм. Какой длины верёвку надо привязать к ручке ведра, чтобы зачерпнуть из проруби воду? Плотность льда b = 900 кг\м куб, морской воды b1= 1030 кг\м куб.
Решение: rgV2-rg(V1+V2)=0 ----условие плавания тел на пов-ти.
Тело погруж-ся на столько на сколько его вес = весу жидкости в объёме его погруж-й части.
rSh- g(SH)=0
h=Hrл /rв
L=H-h=H(1-rл/rв)=1.17м
Ответ: L=1,2м
20
В сосуд цилиндрической формы налиты равные массы воды и машинного масла. Общая высота обоих слоёв жидкостей h= 40 см. Определите давление жидкостей на дно сосуда. bв= 1000 кг\м куб ; bм=900 кг\м куб.
Решение: P=P1+P2
P1=gh2r1-давлениеводы
P2=gh2r2-давление масла
P=g (h1r1-r2h2 h1+h2=40
V=Sh ;m=Vr ; m1=m2 ; Sh1r1=Sh2r2; h1/h2=r2/r1 ; h1= h2 r2/r1
…h2= hr1/(r2-r1) P=g(hr1r2) / r1+r2.+rrrrr
R 2*100*900*10*0.4 / 1900
Ответ: P=3.8*1000 па
54
Два сосуда соединены трубкой, имеющей кран. В первом сосуде находится m1= 2кг некоторого газа под давлением р1= 400 кПа, во втором – m2=3 кг того же газа. Когда кран открыт, в сосуде установилось давление р= 600 кПа. Каким было первоначальное давление р2 газа во втором сосуде? Т= const.
Решение: P3=P1+P2 –закон Дальтона T-const.
P1,P2—парциальные давления.
P1 / P’1=(V1+V2) / V1 ; P2 / P’2=(V2+V1) / V2
P’1=V1*P1 / (V1+V2) P’2=P2V2 \ (V2+V1)
P3= (V1P1+V2P2) / (V1+V2) ; V= m / r ; P3=(m1P1+m2P2) / (m1+m2)
Отсюда P2=(P3(m1+m2)-m1P1) / m2=735*1000=735000 Па
Ответ : P2=735000 Па
55
Герметично закрытый сосуд полностью заполнен водой при температуре
t=27 град С . Каким стало бы давление внутри сосуда, если бы внезапно исчезли силы, взаимодействия между молекулами воды?
Решение : Если бы внезапно исчезли все силы взаимодействия между молекулами воды, то это был бы ид-й газ. Следовательно можно воспользоваться уравнением Менделеева-Кл.
ПV=m/M*RT следовательно P=rRT/M Mr=18
P=1000кг/м * 8,31 дж/мольК * 300К / 0,018 кг/моль =138,5*1000000 На
Ответ : 138500000 На
56
В баллоне объёмом 10 л находится водород под давлением 10 Мпа пр температуре 20 град с. после сгорания ( соединения с кислородом) части водорода образовалось 0,45 кг воды. Сколько газа осталось в баллоне?
Решение : PV=m/M*RT
M1=PVM / RT такая масса водорода находилась в балоне до сгорания
Узнаем сколько потребовалось водорода для образования 0,45 кг воды (m2)
M(H2)=2 ; M(H2O)=18
w (%)=2*100% /18=11%
m2=0.45*0.11=0.05 кг водорода понадобилось для образования 0,45 кг воды
m1=10000000*0.01*2*0.01 / 8.31*293 = 0.08 кг
dm=m1-m2=0.08-0.05=0.03кг
Ответ: dm=0.03 кг.
57
Воздушный шар объёмом V= 200 м куб. парит вблизи поверхности Земли. Когда с шара сбросили балласт, шар поднялся на высоту, где плотность воздуха вдвое меньше. При этом объём шара увеличился в 1,5 раза . Определите массу сброшенного балласта. Плотность воздуха у поверхности Земли b=1,2 кг\м куб
Решение : !) условие того, что шар парит в воздухе. Mg=Fа
..(m1+m2)g=gVr следовательно m2=Vg-m1
2) запишем условие, что шар парит на высоте без баласта.
..m1g=S/2*1.5Vg след-но m=3rV/4
m2=Vr-3Vr/4=Vr/4
m2=(200м*м*м*1,2кг/м*м*м )/ 4=60кг
Ответ: 60кг.
58
Для дыхания человеку в сутки требуется примерно m= 1 кг кислорода. В помещении какого объёма в воздухе при нормальном давлении и температуре
T= 20 град. С содержится такое количество кислорода? Считать, что воздух на 4\5 состоит из азота ( М1= 0,028 кг\ моль) и 1\5 – из кислорода (М2= 0,03 кг.моль).
Решение: Мв=0.029 кг/моль
1/5m1=m2
PV/T=mR/M V=mRT/PM ; V=5*8.31*293 /100000*0.029=4.2 м*м*м
Ответ 4.2 м*м*м
59
Маленький пузырёк воздуха всплывает со дна озера глубиной h= 25 м. Во сколько раз увеличится объём пузырька за время его всплытия от дна до поверхности воды? Атмосферное давление нормальное. Температура воды у дна t1= 15 град С, у поверхности воды t2= 25 град С.
P1=ghr+P0 P2=P0
T1=288К T2=298K
P1V1/T1=P2V2/T2 V2/V1=P1T1 / P2T2 =( rgh+P0)*T2 / P0T2
V2/V1=(1000*10*25+105)T2/105T1 = (250000+100000)Па*298K / 100000Па*288K
V1/V2=3.6 раза
Ответ 3.6 раза
60
Плотность атмосферы с удалением от поверхности Земли уменьшается. Допустим, что плотность воздуха и его температура от высоты не зависят – имеют такие же значения, как у земной поверхности. Какова была бы в этом случае толщина слоя воздуха вокруг нашей планеты? Вычмсления сделайте для нормальных условий. М= 0,029 кг\моль.
P=RTr / M след-но r=PM / RT 61
Найдите формулу соединения азота с кислородом (NxOy), если 1 г этого соединения в газообразном состоянии в объёме 1 л создаёт при температуре 17 град С давление 31,7 кПа.
PV=mRT/M M=mRT/Vr=76
X*14+y*16=76 x=2 y=3
N2O3
62
В подводной лодке для погружения и всплытия имеются 2 сообщающихся между собой резервуара. В погруженном состоянии один резервуар ёмкостью V1 заполнен водой, во второй, ёмкостью V2 , находится сжатый воздух. Каково должно быть минимальное давление сжатого воздуха, чтобы для вспытия лодки с глубины Н , он полностью вытеснил воду из балластной цистерны? Атмосферное давление нормальное.
`Давление должно быть ….. чтобы давление воздуха, который занимает собой 2-резервуара, равнялось гидростатическому давлению на глубине H
P0+gHr=P2 T-const
Закон Бойля –Мариотта: P2V’2=P’1V’1
(P0+ghr)*(V1+V2)=P1V2
P1=(V1+V2) / V2 (P0+ghr)
Ответ P1=(V1+V2) / V2 (P0+ghr)
63
Газовая смесь, состоящая из м1=64 г кислорода и м2=82 г водорода, при температуре t= 17 град С имеет давление р=90 кПа. Определите плотность смеси газов.
По закону Дальтона P=P1+P2
P1V1=m1RT1 / M1 P2T2=m2RT2 / M2
V1=V2=V T1=T2=T
P=RT/V(m1/M1 + m2/M2) ; V=RT(m1/M1 + m2/M2) / P
Т,к r=m/V=(m1+m2) / V
r=(m1+m2)P / (m1/M1+m2/M2)RT=7200/14459.4
Ответ 0,49 кг/м*м*м
64
Баллон для газовой плиты объёмом V=5 л содержит м=500 г пропана (С3Н8) под давлением р=2 Мпа. Температура t= 20 град С. Что можно сказать об агрегатном состоянии пропана в баллоне?
r=m/V=100кг/м*м*м
PV=mRT/M ; M=mRT/PV=0.121кг/моль
M(C3H8)=44*0.01кг/моль
Сравнив с агригатным состоянием придём к выводу, что там жидкость.
87
Холодильник, потребляющий электроэнергию мощность р, за время Т превратил воду в лёд. Какое количество теплоты Q передал холодильник воздуху в комнате, если масса воды м , а её начальная температура t? Теплоёмкость самого холодильника не учитывать.
Aз=PT
Aп=cmT+lm=m(ct+l)
из закона теплового баланса следует
Q==Aз-Ап=PT-m(ct+l)
Ответ Q= PT-m(ct+l)
88
В калориметре содержится м1= 250 г воды при температуре t1=15 град С. в воду бросили м2= 20 г мокрого снега, (его температура 0 град С) В результате темература в калориметре понизилась до t2=10 град С. Какую массу воды содержал снег? С= 4000 Дж\ кг к; l= 3,3 * 10 в 3 Дж\кг.
lm+cm(t3-t2)=cm1(t1-t3)
m=c(m1(t1-t3)-m2(t3-t2)) / l = 0.013кг
m3=m2-m
m3=0.02кг-0,013кг=0,007кг
Ответ 0,007кг
89
Кусок льда массой м=200 г и температурой t=0 град С поместили в нагреватель. Через 10 мин в нагревателе закипела вода. Определите мощность нагревателя, если его КПД равен 60%. С=420 Дж\кг к; l = 3,3 * 10 в 5 степени Дж\кг.
Q=ml Q2=cmt t=100K
Q=ml+cmt=w+A
A=3/5m(l+ct)
N=A/T=5*m(l+ct) / 3T
Ответ N=A/T=5*m(l+ct) / 3T
90
В калориметр, содержащий м1=1 кг воды при температуре t1=20 градС, внесли м2= 10 кг расплавленного свинца при температуре плавления T2= 600 К. Найдите массу воды, превратившейся в пар. Теплоёмкостью калориметра пренебречь. Постоянные для воды: С1= 4200 Дж\кг к, s=2,26 МДж\кг, для свинца : C2= 130 Дж\кг к, l= 25 кДж\кг.
c1m1(q-T1)+rm3=m2l+c2m2(T2-Q)
q=373K m3=m2(l+c2(T2-Q))-c1m1(q-T1)) / r= 0.09кг
Ответ 9 граммов
91
С горы, образующей с горизонтальной плоскостью угол a=30 град, скатываются санки массой м=60 кг. Проехав по склону горы расстояние L=40 м, санки приобрели скорость V=5 м\с. какое количество снега расстаяло за счёт тепла , выделившегося при трении полозьев о снег? Температура t=0 град С,
l=0,33 МДж\кг.
L=V*V / 2a ; a=V*V/2L=0.3м/с*с
Ma=Fтр+N+mg
X: ma=mg*sina-Fтр
Y: N=mgcosa
Ma=mgsina-Kmgcosa
Kgcos=gsina-a k=tga-a/gcosa
K=0.47
Aтр=kmgcosa*r=9500дж
A=Q m=Q/l=A/l ; m=9500 / 0.33*1000000 кг
Ответ m=0.03кг
92
Вода при температуре t=0 градс находится в сосуде, из которого быстро откачивают воздух. Вследствие интенсивного испарения происходит замерзание воды. Какая часть первоначального количества воды в результате превратится в лёд , а какая часть воды испарится ? r = 2,26 МДж\ кг, l= 0,33 МДж\кг.
..m1-масса воды переведённая в лёд
m2-масса воды, пре-я в пар
необходимая для образ-я кол-во теплоты здесь может быть получено только за счёт того, что при замерзании воды выд-ся теплота Q1=Q2 m1l=m2r
m2=m1l/r
m1+m2=m ; m= m1+m1l/r ; m1=mr/ (r+l)=0.88 кг m1=m2r/l
m=m2+m2r/l=m2(1+r/l)=m2(l+r) / l
m2=lm /(r+l) ; m2=0.12 кг
Ответ m1=0.88кг ; m2=0,12кг
93
При скорости V=72 км\час, автомобиль расходует м=5,5 кг бензина на 100 км пути. Определите мощность, развиваемую двигателем, если его КПД h=25%.
Удельная теплота сгорания бензина q=45 Мдж\кг.
Q=qm
A=uQ Vt=S t=S/V
N=uQ /t =12.5 кВт
Ответ N= 12.5 кВт
94
автомобиль массой М имеет бензобак ёмкостью V. Какое расстояние S может проехать автомобиль после полной заправки бака горючим? Сила сопротив-ления, действующая на автомобиль с постоянной скоростью, составляет n-ную часть его веса. КПД двигателя h . Плотность бензина р, удельная теплота сгорания q .
h=Aп/Aз=FscosL / gm ; L=0 ; cosL=1
0=Fт+N+Mg+Fс
x: Fт=Fс y: N=Mg
|P|=|N| Fт=Fс=kMg h=MgSk / gm=MgSk / gVr ; m=Vr
Ответ : S=MgSk /gVr
95
Газ , занимающий объём V1=1л при давлении р1= 2 атм, расширился изотермически до объёма V2=2л. Затем при этом объёме давление газа было уменьшено в два раза. Далее газ расширился изобарически до объёма V4= 4 л.
Начертите график зависимости давления р газа от его объёма V . используя график определите при каком из перечисленных процессов газ совершит наибольшую работу.
1) P1V1=P2V2 T-const
P2=P1V1/V2
2) V-const
3) P-const
при переходе 1-2 газ сов-т наиб работу
это опред-т площ-дь крив-й трапеции.
При переходе 2-3-A=0. Т,к V=0
При перходе 3-4 работа опред-ся площ-ю заштрих-ого прямоугольника. Из графика видно, что А(1-2)>A(3-4)
96
Газовый баллон , объёмом V=15 л, содержит гелий при температуре t=27 градС и давлении р=15 атм. Вычислите среднюю энергию одной молекулы гелия, а также энергию теплового движения всех молекул газа в баллоне.
Eш=3/2KT ;
PV/T=mR/M ; m=PVM/TR =0.018 кг
…m0=M/Nа
N=m/m0
E=EшN =33.5кдж
Ответ E=33.5кдж
97
Один моль одноатомного газа, температура которого t=27 градС занимает объё V=0,5 л. какое количество теплоты сообщили газу, если в процессе расширения при постоянном давлении его объём увеличился в 3 раза?
Q=U+A ; P-const
Q=3/2VRT+PV
V1/V2=T1/T2 ; T2=V2T1/V1=3T1
..dT=3T1-T1=2T1
PV=nRT ; Q=2.5nRT=5nRT1
Q=5*1моль*8,31дж/мольК*300=12500дж
Ответ Q=12,5кдж
98
При изобарическом нагревании азота м=2кг на dТ = 50К. Газу было сообщено Q1=50 кДж. Теплоты. Какое количество теплоты Q2 потребуется для такого же нагревания азота при постоянном объёме?
Q=1.5nRT+nRT=2.5nRT
Q=1.5nRT
Q*3/5=Q2 Q2=30кдж
Ответ Q=30кдж
99
Идеальная тепловая машина , работающая по циклу Карно получает от нагревания Q1= 130 Дж тепла и совершает работу А=30Дж. На сколько надо изменить температуру охладителя при неизменной температуре t=327 град нагревателя, чтобы увеличить КПД машины в два раза?
h1=A1/Q1*100%
h2=2A1/Q1*100%
m2=(T1-T2)/T2*100% след-но 2A1/Q1=(T1-T2)/T1
T2=T1(1-2A1/Q1)
h=(T1-T2)/T1*100% ; A1/Q1=(T1-T2)/T1
T2=T1(1-A1/Q1) T1-темпер-ра хол-ка до сов-я работы
Т2-т-ра после работы
…dT=T2-T1=-T1A1/Q1 минус показ-т, что темпер-ру надо уменьшить.
…dT=140K
Ответ Т=140К
100
Нагревателем идеальной тепловой машины служит резервуар, в котором происходит конденсация водяного пара при температуре 100 град. Тепло передаётся охладителю, содержащему лёд с температурой 0 град. За время работы машины в нагревателе образовалось 2 кг воды. Какое количество м2 льда расстаяло при этом в охладителе? g(гамма) = 2,26 МДж\кг. l=0,33 Мдж\кг.
Q1=rm1 ; Q2=lm2
Rm1=lm2 ; m2=rm1/l=13.7кг
Ответ m2=13.7 кг
1.Электростатика
2.Электрический ток
3.Магнетизм
21
Два разноимённых точечных разряда q и -4q находятся на расстоянии 25 см друг от друга. Определите положение точки пространства в которой напряжённость электрического поля , созданного обоими зарядами равно 0.
Принцип суперпозиции. Eо=E1+E2=0
E1=q/4ПeT1*T1 E2=(-4)q/4Пr2*r2*e след-но q/4Пe(1/r1*r1- 4/r2*r2
4r1*r1=r2*r2 2r1=r2 r1=x r2=d+x x=d=0.25м
Ответ: на прямой заряды на расстоянии x=0.25м от заряда q
22
плоский воздушный конденсатор , пластины которого расположены вертикально, погрузили до половины в жидкий диэлектрик. Во сколько раз увеличилась ёмкость конденсатора, если диэлектрическая проницаемость жидкости e= 5,0?
C=Se/d ; e=1
Cо=C1+C2 при пар-ом соед.
C1=(S*1/2*e)/d C2=(e*e*S*1/2)/d
Cо=Se(1+e)/2d Cо/C=(1+e)/2=3
Ответ: 3
23
Заряженная пылинка массой 3 *10 в минус 14 степени кг , находится в равновесии между горизонтальными пластинами плоского кондесатора. Расстояние между пластинами 5,3 мм , напряжение U1=480 вольт. После облучения ультрафиолетовыфм светом, пылинка теряет часть заряда и начинает опускаться, чтобы восстановить равновесие. Напряжение (U2 ) увеличили до 505 вольт. Какой заряд потеряла пылинка?
F=mg F=qE E=u/d
q1=mgd/u1 q2=mgd/u2 dq=q1-q2 dq=mgd(1/u1-1/u2)
dq=16408.8*((10) в минус23)
Ответ: 16*((10)в минус 20)
24
Бусинка массой 100 мг и зарядом q= 16,7 нкл, подвешена на нити. На какое расстояние надо поднести к ней снизу равный по величине одноимённый заряд, чтобы сила натяжения нити уменьшилась вдвое.
T2=mg-F где F=1q1*q1/4Пe1*e*r*r F=mg/2 mg/2=q1*q1/4Пr*r*e1*e
…r=q(1/2Gmge1*e) под корнем=0.07м
Ответ:0,07м
25
Конденсаторы ёмкостью равные С1= 2 мкф и С2= 3 мкф, включены в цепь напряжением U=110 вольт. Определите заряд , напряжение между обкладками и энергию каждого конденсатора, если они соединены а) параллельно;
б) последовательно
U=U1=U2=110B
C=q/u c1=q1/u1 q1=c1*u1=220*((10)в минус 6)Кл q2=c2*u2=330*((10)в минус 6)Кл W1=q1*u1/2=220*((10)в минус 6)*110/2m=12,1*((10)в минус 3)Дж W2=330*((10)в минус 6)*110/2=18,15*((10)в минус 3)Дж
Б) При послед-м соед. Заряды на обоих конденс-х одинаковы) q1=q2=q
F1-f2=q/c1=u1 f2-f3=q/c2=u2 f1-f3=q(1/c1+1/c2) f1-f3=u
…q=u/(1/c1+1/c2)=1.3*((10)в минус 4)Кл f1-f3=u
u1=q/c1=65B u2=q/c2=43B W1=c1*u1*u1/2=4.2*0.001Дж
W2=2.8*0.001Дж
26
Конденсатор, ёмкостью С1=5 мкФ , заряжен до разности потенциалов U=50V и отключён от источника напряжения. Параллельно к нему подсоединён второй конденсатор ёмкостью 10мкФ . найдите энергию искры , проскактвающей при соединении конденсаторов?
Q=c1*u=25*0.00001Кл
W1=c1*u*u/2 W1=6.25*0.001Дж
При соединении Со=С1+С2=15*0,000001Ф
W=q*q/2e W2=2.08*0.001Дж
Из закона сохр-я энергии W=W1-W2=4.2*0.001Дж
Ответ: 4.2*0.001Дж
27
Конденсатор С=20 мкФ, напряжение между пластинами которого равно u=70V, разряжается через два параллельно соединённых резистора М1=5Ом, М2=20Ом.
Какое количество теплоты выделится в каждом резисторе?
W=c*u*u/2=49*0.001Дж
Из закона сохранения энергии Q1+Q2=W
Q1/Q2=R2/U2*U2=R2/R1 Q1/Q2=4 след-но Q1=4Q2
Отсюда 5Q2=50*0.001Дж Q2=0.01Дж Q1=4*0.01Дж
Ответ: 0,01Дж ; 0.04Дж
28
В пространстве, где одновременно созданы вертикальные и горизонтальные электрические поля Еv= 300 V\м, а Еg=400V\м. Вдоль линии напряжённости , результирующей эти два поля летает электрон. При прохождении пути S=2.7 мм, его скорость изменилась в два раза. Определить конечную скорость электрона.
E=E1+E2=500 В/м
На электрон действует сила F=qE она сообщ-т ускорение ma=-|e|E=eE a=eE/m
3/4V*V=2aS V=(8*e*E*S/3*m)под корнем=25*10000*((10)в ½-й степени) м/с
Ответ: V=8*((10)в степени 5) м/с
59
Из проволоки , имеющей сопротивление 64 Ом, сделано кольцо. В каких точках кольца следует подключить провода, чтобы подключить сопротивление R=12Ом.
1/R=1/R1+1/R2 R=R1*R2/R1+R2 R1+R2=Rо
R1*R2=R(R1+R2)=R*Rо=768((ом)в квадрате) R1=48 ом R2=16ом
R1+R2=64
R*Rо=768 провода надо подс-ть так
L/Rо=L1/R1=L2/R2 L1=R1*L/Rо L2=L*R2/Rо
L1/L2=R1/R2=3
Ответ: места соед-я отдел-т уго=90 градусов
60
Катушка диаметром Д=15 см, содержит 500 витков МЕДНОГО ПРОВОДА. Предельно допускаемая плотность тока для меди равна 10 А\мм квадратн.
Какое максимальное напряжение можно приложить к катушке. Р=17 кОм\м
J=I/S. Где I=U/R
Umax=jrL
L=GdN Umax=jrПdN=40B
Ответ: 40B
61
К аккумулятору с внутренним сопротивлением 0,01 Ом подключён резистор с сопротивлением 10 Ом. Вольтметр даёт одинаковое показание при последовательном и параллельном подключении его к резистору. Найти сопротивление вольтметра.
I=e(R+r)
А) e=I(R1*R/(R1+R) +r) U=Ire
Б) e=I2(R1+R+r) U=IR
62
Имеются два вольтметра с сопротивлением 15 кОм и 20 кОм, рассчитанные на максимальное напряжение 100V и 80V. Какое наибольшее напряжение можно измерить с помощью этих вольтметров.
R2=R1(Umax/U1-1)
Umax=(R2/R1+1)U1
Umax=(R1/R2+1)U2=140
63
Батарея аккумуляторов, имеющая внутреннее сопротивление 1)м, замкнута на резистор. При этом нпряжение на зажимах батареи 20 V. При нормальном подключении ещё одного такого же резистора напряжение падает до 15 Ом.
U=eR/(R+r) R2=R1/2 след-но U1=eR/(R+r) ; U2=R*1/2e/(R*1/2+r)
Отсюда e=U1(R+r)/R e=U2(R*1/2+r)/R*1/2
Отсюда U1(r+R)=2U2(R*1/2+r)
R=r(2U2-U1)/(U1-U2)=2 ом
Ответ: 2ом
64
Два резистора сопротивлением 12,5 Ом и 2 Ом подключают к источнику тока последовательно, затем параллельно. В обоих случаях в цепи выделяется одинаковая мощность. Найти внутреннее сопротивление источника тока.
R3=R1+R2=14.5 ом
Б) Пар-но R4=R1*R2/(R1+R2)=1.7 ом
I=e/(R+r) P=I*IR
P3=(e/(R3+r)в квадрате) ;P4=((e/(R4+r)в квадрате)*R4
P3=P4 R3/(R3+r)*(R3+r)=R4/(R4+r)*(R4+r)
(R4+r)/(R3+r)=((R4/R3)под корнем) ; подставим значение R4 и R3
(r+1.7)/(r+14.5)=0.35 откуда r=5 ом
Ответ: 5 ом
65
Сила тяги электровоза при скорости 13 м\с равна 380 кН. Найти КПД электровоза, если напряжение в контактной сети 3кВа, а сила тока в обмотке какждого из восьми двигателей 230А.
M=Pпол/Pзатр*100%=F*V/nIU*100%=90%
Ответ: 90%
66
Железную проволоку длиной 10м подключили к источнику напряжения 10V. На сколько повысится температурав проволоки через 10 секунд. Зависимостью сопротивления проводника от температуры пренебречь. Плотность железа 7800 кг\ куб. м. Уд. Теплоёмкость 460 Дж\кг*Н
Q1=cmT=rcSLT Q2=U*UT/R=U*UST/rL
Из закона сох-я эн-ии Q1=Q2 след-тcLTSr=U*U*T*S/rL T=U*U*T/L*L*C*P*r=23K
Ответ: 23К
67
В медном проводнике длиной 2 м и площадью поперечного сечения 0,4 кв мм при протекании тока ежесекундно выделялось 0,35 Дж теплоты. Сколько электронов проходит за 1с через поперечное сечение проводника.
Р=17 кОм\м, Е=1,6 *10 в минус 19 степени Кулон
R=rL/s Q1=I*I*R*T=I*I*r*L*T/S I=((Q1S/LT1r)под корнем)
…q=IT N=q/e=It/e=1.27*((10) в 19-й степени)
Ответ: 1,27*((10) в 19-й степени)
68
Электрическая печь для термической обработки деталей имеет два нагревательных элемента. Один элемент нагревает деталь до нужной температуры за t=10 мин. Второй – за 20 ин. Какое время понадобится для нагревания детали, если включить оба элемента. А) параллельно – найдите t3.
Б) последовательно – t4 ?
Q1=Q2=Q а)параллельно Q=Ut1/R1 Q=Ut2/R2 R1=ut1/Q R2=ut2/Q
Подставляя в выражение 1 получаем
R3=U(t1*t2)/Q(t1+t2) след-но t3=t1*t2/(t1+t2) ; t3=4000c
Б) R3=R1+R2=U(t1+t2)/Q t4=t1+t2=30мин
Ответ: T3=4000c ; t4=1800c
69
Какой длины надо взять нихромовую проволоку площадью сечения 0,1 кв мм, чтобы изготовить нагреватель, способный за 3 мин нагреть 200 гр воды от 10 до 100 град С. Напряжение равно 220V. Р=100 мкОм\м, С=4200 Дж\кг*Кград ?
Q=cmT eh-bt ntgkjdjuj ,fkfycf Q1=Q2
Q=U*Ut/R cmT=U*U*t/R
R=rL/S=U*Ut/cmT; L=U*U*St/cmTr=0.11 м
Ответ: 11*((10) в минус 2-й)
70
Электродвигатель стиральной машины нагревает воду в 20 л банке от 10 град до 80 градС. На сколько квт-час увеличатся показания электросчётчика, если на другие операции машина израсходовала ещё W=0,5 квт-час. Какова стоимость всей стирки. Цена одного квт-час 0,15 руб. Уд. Теплоёмкость воды 4200Дж\кг*Кград
M=Vg=20кг Q1=cmt=5880*1000Дж
W=Q1=5880000 Вт*с (из закона сохр-я энергии)
W=W1+dW=2.1 кВт*ч
Ы=2,1кВт*ч*0,15=0,32руб
Ответ: dW=1.6кВт*ч , Ы=0,32руб
71
Мощность выделяющейся во внешней цепи аккумулятора при токе силой 1А равна 5вт , а при токе силой 0,5А, мощность равна 3,75вт. Определите величину тока короткого замыкания.
I=e/(R+r) U=e-Ir P=IU U=P/I=e-Ir
P1/I1=e-I1r ; 5=e-r
P2/I2=e-I2r ; 7.5=e-0.5r r+5=7.5+0.5r r=5 ом e=10B
При коротком замыкании R------0 след-но R+r=r Iк.з=e/r=2A
Ответ: 2A
72
Электрический насос, работающий от сети напряжением 220В, качает воду из колодца, глубиной 10 м. За время работы 1час , объём откаченной воды составил 10,9 куб м. Определить КПД, если сила тока 1,67А.
m=Aп/Aз
Aп=Eп2-Eп1=mgh=Vghr
Aз=Iut m=Vghr/Iut*100%=82%
Ответ: 82%
89
Горизонтальные рельсы находятся в вертикальном однородном магнитном поле с индукцией 0,1Тл. При L=30 см. Поперек рельсов лежит металлический стержень массой 30кг. Коэффициент трения между рельсами и стержнем равен 0,2. Какой силы ток необходимо пропустить по стержню, чтобы он сдвинулся с места.
Fа=IBL
Fтр=kmg
Чтобы проводник сдвинулся с места необходимо чтобы Fа>Fтр
IBL=kmg
I=kmg/BL=20A
Ответ I>20A
91
Электронный протон, ускоренный одинаковой разностью потенциалов, влетает в однородное магнитное поле, перпендикулярно линиям индукции. Во сколько раз различаются радиусы кривизны траектории электрона и протона.Масса электрона 9,1*10 в минус 31 степени кг, масса протона – 1,67 *10 в минус 27 степени кг.
R=mV/qB где V=((2q(f1-f2)/m) под корнем R=(m*m*2q(f1-f2)/q*qmB*B )
Под корнем
R1=(2m1(f1-f2)/q*B*B) под корнем R2= (2m2(f1-f2)/q*B*B) под корнем
R1/R2=(m1/m2)под корнем=0,4*100=40
Ответ: 40
92
Циклотрон предназначен для ускорения протонов до энергии 5 мВ. Индукция однородного магнитного поля перпендикулярно которому движутся частицы ускорителя В=0,5 Тл. Определите наибольший радиус орбиты протона. Е=1,6*10 в минус 19 степени кулон, М= 1,67 *10 в минус 27 степени кг.
R=mV/eB
E=m*V*V V=(2E/m)под корнем
R=(2Em/eB)под корнем
E=5мэв=5*1000000*1,6*((10) в минус19-й степени)Дж=8*((10) в минус 13-й степени)
R=0.64м
Ответ:Rmax=0.64 м
93
Магнитный поток, пронизывающий замкнутый проволочный контур, сопротивлением 0,5 Ом, равномерно увеличился с 0.2 мвв до 1 мвв. Какой заряд прошёл за это время через поперечное сечение проводника.
При равномерном движ-ии сила тока,эдс-постоянны
Из закона электро-магнитной индукции |e|=df/t I=e/R=df/tR
Отсюда dq=df/R=(f2-f1)/R=1.6*0.003Kл
Ответ: dq=1.6*0.003Кл
94
Проволочное кольцо из алюминия диаметром 25 см находится в однородном магнитном поле. Индукция, которая возрастает за 1 сек на 2 Тл. Плоскость кольца перпендикулярна линиям магнитной индукции. Определите толщину проволоки, если сила индукционного тока в кольце 12А. Уд сопротивление алюминия 26 нОм\м.
f=BS
e=BS/t из закона электро-маг-й индукции I=e/R R=e/I=BS/It, гдеS=ПD*D/4
R=BПD*D/4tI=rL/S=rПD/ПD*D/4=4rD/d*d
…d=(16Itrt/ПBD)под корнем=18*0,0001 м
Ответ: d=18*0.0001м
95
В замкнутое проволочное кольцо вводят магнит сначала быстро, затем медленно. Доказать, что в обоих случаях по кольцу протекает одинаковый заряд. Одинаковое ли количество теплоты выделится.
I=q\t=e/R e=f/t
…q=df/R как видно заряд не зависит от времени внесения в кольцамагнита
q-const
Q=I*Irt=dq*qRt/dt*t=dq*qR/dt
Видно Q~1/dt
-чем меньше t, тем больше Q
-чем болше t, тем меньше Q
Ответ: q-const; нет
Оптика . Квантовая физика. Атомное ядро.
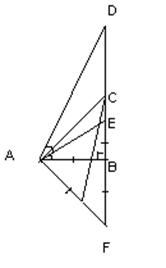
30. Человек удаляется со скоростью v= 2,0 м/с от уличного фонаря, находящегося на высоте Н= 8,5 м от поверхности Земли. В некоторый момент времени длина тени человека составляла Ь=1,3 м, а через t = 1 с — стала d = 1,8 м. Найдите рост человека. ^Ч inn-
DF=VT=2м
D/S=CB/H ; b/S=Be/H ; eB=FB+b ; CB=d+2+FB
…d/CB=S/H ; b/eB=S/H заменим С подставкой
d/(d+2+FB)=b/(Fb+b) ; (Fb)d+bd=bd+2b+Fb*b
FB=(d-b)=2b ; Fb=2b/(d-b)=5.2 ; b/S=eB/H ; S=Hb/(FB+b)=1.7 м
Ответ: 1,7м
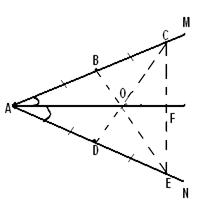
31. Сколько изображений получится от светящейся точки в двух плоских зеркалах, образующих между собой прямой угол? Сколько будет изображений, если точку поместить между параллельными зеркалами?
Выполняя последовательно построения изображ-й т-ки Ао, в зеркале 1,2, Найдём, что А1 является изображением точки Ао в зеркале 2ж а А2 в зеркале 1.
А3-изображение точки А1 в зеркале 1
А3 изображение точки А2 в зеркале2
Они совпадают, т.к Ао,А1,А2,А3-прямоугольник
Ответ: R=3
32. На дне сосуда, наполненного водой до высоты Н, находится точечный источник света. На поверхности воды плавает круглый непрозрачный диск так, что центр диска находится над источником света. При каком минимальном радиусе R диска свет не будет выходить через поверхность воды? Показатель преломления воды п. 33. Столб вбит вертикально в дно реки глубиной Н = 2 м. Над поверхностью воды столб возвышается на h = 1 м. Какова длина тени столба на дне реки, если высота Солнца над горизонтом <р= 30° ? п=1,33.
При определении a свет ни будет выходить из воды b=90 sin90=1
Sina/sinb=1/n ; a-пред-й угол отражения sina-1/n В то же время sina=AO/AB ; AO=R
AB=R/sina=Rn
Из теоремы Пифагора R*R=A*B*B-H*H=R*R*n*n-H*H
R=((Rn)*(Rn)-H*H)под корнем
Ответ: R=((Rn)*(Rn)-H*H)под корнем
34. При определении на глаз по вертикальному направлению глубина реки кажется равной h = 1,5 м. Какова истинная глубина реки?
АВ=Htg=h*tgb ; H=AS ; h=AS ;
H/h=tgb/tga
a и b, малы ; tgb/tga=sinb/sina=n ; H/h=n H=hn=1.95м
Ответ: H=hn=1.95м
35. Солнечные лучи, проходя через маленькую прорубь во льду, освещают дно озера. Расстояние между точками дна, куда попадают лучи сразу после восхода и перед заходом Солнца в день весеннего равноденствия, L= 3 м. Определите глубину озера. Показатель преломления воды п = 1,3.
b’=b; A’OB=AOB
A’O=AO=h/r=1.5м
tgb=AO/H ; H=AO/tgb ;tg50=1.192
H=1.5/1.192=1.26м
Ответ: H=1.5/1.192=1.26м
36. По дороге со скоростью v = 54 км/ч движется автомобиль. Его фотографируют с расстояния L = 10 м от дороги (и от автомобиля). Размытие изображения на пленке не должно превышать величину d = 50 мкм. Каково должно быть время экспозиции Дг, если фокусное расстояние объектива F = 40 мм ?
Лин увел. Линзы I=d/S=f/L S=Ld/f
1/f=1/a+1/L ; f=LF/(l-F)
S=Ld(LF(L-F=d(L-F)/F
T=d(L-F)/FV=0.00083 cсек.
Ответ0,00080ск
37. Свеча расположена на расстоянии L = 2,5 м от экрана. Собирающая линза дает на экране четкое изображение свечи при двух положениях, находящихся на расстоянии а = 50 см друг от друга. Определите оптическую силу D линзы.
F+d=3.5 м ; d+0.5=d’ f-0.5=f’
D=1/f+1/d=(f+d)/fd D=1/f’+1/(d*d)=(f’+d’)/f’d’
D=L/fd ; D=L/f’d’
F+d=2.5
Fd=(f-0.5)(d+0.5)
(2.5-d)d=(2-d)(d+0.5)
2.5d-d*d=2d+1-d*d+0.5d
d=1 f=1.5
Отсюда D=2.5/1.5=5/3 ДПТР
Ответ 5/3 ДПТР
38. Горящая лампочка находится на расстоянии d = 0,9 м от центра экрана. Можно ли получить отчетливое изображение нити лампочки в центре экрана, используя для этого собирающую линзу с фокусным расстоянием F = 24 см ?
Изображение должно быть отчётливое увеличенное
1/F=1/f+1/d
f+d=L
fd=FL если эта система имеет решение, то можно получить отчётливое
f+d=L изображение нити, если нет то нельзя, т.к не найдётся точного расположения . fd=0.216
f+d=0.4
d*d-0.9d+0.216=0
Д<0 система не имеет реш-й следовательно Нельзя
Ответ Нет39. При фотографировании человека с расстояния di = 15 м его изображение на фотопластинке получилось высотой hi = 30 мм, а с расстояния d2 = 9 м — высотой hz = 51 мм. Определите фокусное расстояние объектива фотоаппарата.
Г=|F| / |d1-F|=H/R ; F>0 ; d-F>0
F/(d1-F)=h1/H ; F/(d2-F)=h2/H
Jnc.lf h1(d1-F)=h2(d2-F)
F=(h2d2 - h1d1) / (h2-h1)=0.42 м
Ответ F=0. 42м
40. На собирающую линзу с фокусным расстоянием Fi падает пучок лучей, параллельных главной оптической оси. На каком расстоянии от собирающей линзы надо поместить рассеивающую линзу с фокусным расстоянием Fz, чтобы выходящие из нее лучи вновь стали параллельны главной оптической оси? Фокусные расстояния линз относятся, как Fi:F2 =3:1.
Для собирающей линзы имеем 1/f1+1/d1=1/F1
Считая, что d=бесконечности
Поэтому 1/f1=1/F1. Откуда F1=f1
Следовательно изображение нах-ся в орогизе линзы и является источником для расс. Линзы
Для рассеевающей линзы –1/f2+1/d2=-1/F2
…d2=L-F1 f2-бесконечность след-но
1/(L-F1)=-1/F2 F1-L2=F2 L2=F1-F2=2F2
Ответ 2F2
Похожие работы
... математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной ...
... , символисты). ЭТА ИНФОРМАЦИЯ МОЖЕТ БЫТЬ ПОЛЕЗНОЙ ДЛЯ ВАС!Вашему вниманию представляется набор фалов, которые сосредотачивают в себе порядка 99% ответов на экзаменационные вопросы в разных редакциях по философии на вступительный экзамен в аспирантуру НТУУ «КПИ» (Киевский Политех.) по программе 2001-2002гг. (может быть эта программа была и раньше, может сохранится и в будущем, но на эти годы ...
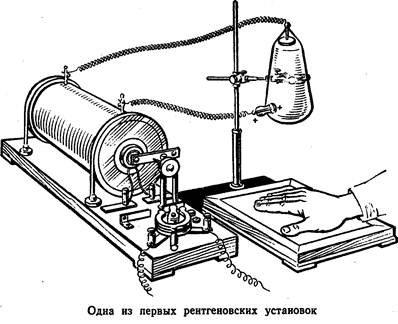
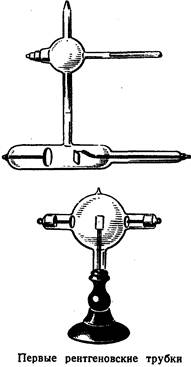
... П. Только одну награду принял он с радостью и волнением. Это была Нобелевская премия по физике. К. Рентген стал в 1901 г. первым Нобелевским лауреатом. Сейчас эти премии хорошо известны: они вручаются крупнейшим ученым за фундаментальные открытия в области физики, химии, биологии, медицины. К настоящему времени восемь советских физиков удостоены этого высокого звания: И. Е. Тамм, И. М. Франк, ...
... – педагогический эксперимент. Эксперимент проходил в три этапа: 1 этап – констатирующий эксперимент. При его проведении были выявлены знания учащихся по теме «Использование и измерений и решение задач на местности при изучении некоторых тем школьного курса геометрии», при этом использовались различные формы и методы выявления знаний, такие как: анкетирование, беседы с учащимися и учителями, ...


0 комментариев