Свободное падение тел. Ускорение свободного падения
Третий закон Ньютона
Импульс тела. Закон сохранения импульса. Реактивное движение
Простые механизмы (наклонная плоскость, рычаг, блок) их применение
Архимедова сила дня жидкостей и газов. Условия плавания тел
Температура, ее измерение. Абсолютная температурная шкала. Скорость молекул газа
Количество теплоты. Удельная теплоемкость вещества. Закон сохранения энергии в тепловых процессах (первый закон термодинамики)
Испарение и конденсация. Насыщенные и ненасыщенные пары. Влажность воздуха
Электрический заряд. Взаимодействие заряженных тел. Закон Кулона. Закон сохранения электрического заряда
Напряжение. Электроемкость. Конденсаторы
Работа и мощность тока. Электродвижущая сила. Закон Ома для полной цепи
Электрический ток в газах. Виды газовых разрядов и их применение. Понятие о плазме
Закон Ампера. Действие магнитного поля на движущийся заряд. Сила Лоренца
Явление самоиндукции. Индуктивность. Энергия магнитного поля
Превращение энергии при гармонических колебаниях. Вынужденные колебания. Резонанс
Вынужденные электрические колебания. Переменный электрический ток. Генератор переменного тока. Мощность переменного тока
Закон Ома для переменного тока
Электромагнитные волны. Скорость их распространения. Свойства электромагнитных волн
Шкала электромагнитных излучений. Зависимость свойств электромагнитного излучения от частоты. Применение электромагнитных излучений
Дисперсия света. Спектр электромагнитного излучения. Спектроскопия. Спектральный анализ. Источники излучений и виды спектров
Испускание и поглощение света атомами. Лазер
Методы регистрации ионизирующих излучений
Биологическое действие ионизирующих излучений. Защита от радиации. Применение радиоактивных изотопов
Навигация
Явление самоиндукции. Индуктивность. Энергия магнитного поля
Билеты по физике за весь школьный курс
112347
знаков
1
таблица
2
изображения
50. Явление самоиндукции. Индуктивность. Энергия магнитного поля.
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток Ф через контур пропорционален вектору магнитной индукции В, а индукция, в свою очередь, силе тока в проводнике. Следовательно, для магнитного потока можно записать 
. Коэффициент пропорциональности называется индуктивностью и зависит от свойств проводника, его размеров и среды, в которой он находится. Единица индуктивности – генри, индуктивность равна 1 генри, если при силе тока в 1 ампер магнитный поток равен 1 веберу. При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока вызывает возникновение в катушке ЭДС индукции. Явление возникновения ЭДС индукции в катушке в результате изменения силы тока в этой цепи называется самоиндукцией. В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию при включении и убыванию при выключении цепи. ЭДС самоиндукции, возникающая в катушке с индуктивностью L, по закону электромагнитной индукции равна
. Пусть при отключении сети от источника, ток убывает по линейному закону. Тогда ЭДС самоиндукции имеет постоянное значение, равное 
. За время t при линейном убывании в цепи пройдет заряд 
. При этом работа электрического тока равна 
. Эта работа совершается за свет энергии Wм магнитного поля катушки.
51. Гармонические колебания. Амплитуда, период, частота и фаза колебаний.
Механическими колебаниями называют движения тел, повторяющиеся точно или приблизительно одинаково через одинаковые промежутки времени. Силы, действующие между телами внутри рассматриваемой системы тел, называют внутренними силами. Силы, действующие на тела системы со стороны других тел, называют внешними силами. Свободными колебаниями называют колебания, возникшие под воздействием внутренних сил, например – маятник на нитке. Колебания под действиями внешних сил – вынужденные колебания, например – поршень в двигателе. Общим признаков всех видов колебаний является повторяемость процесса движения через определенный интервал времени. Гармоническими называются колебания, описываемые уравнением 
. В частности колебания, возникающие в системе с одной возвращающей силой, пропорциональной деформации, являются гармоническими. Минимальный интервал, через который происходит повторение движения тела, называется периодом колебаний Т. Физическая величина, обратная периоду колебаний и характеризующая количество колебаний в единицу времени, называется частотой 
. Частота измеряется в герцах, 1 Гц = 1 с-1. Используется также понятие циклической частоты, определяющей число колебаний за 2p секунд 
. Модуль максимального смещения от положения равновесия называется амплитудой. Величина, стоящая под знаком косинуса – фаза колебаний, j0 – начальная фаза колебаний. Производные также гармонически изменяются, причем 
, а полная механическая энергия при произвольном отклонении х (угол, координата, и т.д.) равна 
, где А и В – константы, определяемые параметрами системы. Продифференцировав это выражение и приняв во внимание отсутствие внешних сил, возможно записать, что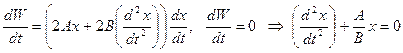 
, откуда 
.
52. Математический маятник. Колебания груза на пружине. Период колебаний математического маятника и груза на пружине.
Тело небольших размеров, подвешенное на нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела, называется математическим маятником. Вертикальное положением является положением равновесия, при котором сила тяжести уравновешивается силой упругости. При малых отклонениях маятника от положения равновесия возникает равнодействующая сила, направленная к положению равновесия, и его колебания являются гармоническими. Период гармонических колебаний математического маятника при небольшом угле размаха равен 
. Чтобы вывести эту формулу запишем второй закон Ньютона для маятника 
. На маятник действуют сила тяжести и сила натяжения нити. Их равнодействующая при малом угле отклонения равна 
. Следовательно, 
, откуда 
.
При гармонических колебаниях тела, подвешенного на пружине, сила упругости равна по закону Гука 
. По второму закону Ньютона 
.
Похожие работы
... закона, а на языке более уважительном и человечном. И вместо “вы обязаны”, будем говорить: “давайте попробуем”»[45]. Школьный курс по основам православной культуры является предметом культурологическим (а не религиозным), и поэтому его нужно преподавать в школе так, как необходимо преподавать математику. Так считает митрополит Смоленский и Калининградский Кирилл (Гундяев)[46]. Реализовывать эту в ...
... раза. В силу специфичности информации схемы определения количества информации, связанные с ее содержательной стороной, оказываются не универсальными. Универсальным оказывается алфавитный подход к измерению количества информации. В этом подходе сообщение, представленное в какой-либо знаковой системе, рассматривается как совокупность сообщений о том, что заданная позиция в последовательности ...
... полезно учителю при подготовке рассказа на уроке. В данной публикации сделана попытка выделить тот самый минимум, который ученику необходимо включить в свой ответ на экзамене. Примечания для учеников При ответе надо быть готовым к дополнительным вопросам об обосновании тех или иных утверждений. Например, каковы максимальное и минимальное значения 8-битного целого числа со знаком и почему их ...
Элективный курс по алгебре для 9-го класса на тему "Квадратные уравнения и неравенства с параметром"
... список или выбрать из 2-3 текстов наиболее интересные места. Таким образом, мы рассмотрели общие положения по созданию и проведению элективных курсов, которые будут учтены при разработке элективного курса по алгебре для 9 класса «Квадратные уравнения и неравенства с параметром». Глава II. Методика проведения элективного курса «Квадратные уравнения и неравенства с параметром» 1.1. Общие ...
0 комментариев