Навигация
Электромагнитные волны. Скорость их распространения. Свойства электромагнитных волн
61. Электромагнитные волны. Скорость их распространения. Свойства электромагнитных волн.
Любое изменение магнитного потока в контуре вызывает появление в нем индукционного тока. Его появление объясняется возникновением вихревого электрического поля при любом изменении магнитного поля. Вихревое электрическое поде обладает тем же свойством, что и обыкновенное – порождать магнитное поле. Таким образом, однажды начавшийся процесс взаимного порождения магнитного и электрического полей непрерывно продолжается. Электрическое и магнитные поля, составляющие электромагнитные волны, могут существовать и в вакууме, в отличие от других волновых процессов. Из опытов с интерференцией была установлена скорость распространения электромагнитных волн, составившая приблизительно ![]() . В общем случае скорость электромагнитной волны в произвольной среде вычисляется по формуле
. В общем случае скорость электромагнитной волны в произвольной среде вычисляется по формуле ![]() . Плотность энергии электрической и магнитной компоненты равны между собой:
. Плотность энергии электрической и магнитной компоненты равны между собой: ![]() , откуда
, откуда ![]() . Свойства электромагнитных волн схожи со свойствами других волновых процессов. При прохождении границы раздела двух сред частично отражаются, частично преломляются. От поверхности диэлектрика не отражаются, от металлов отражаются практически полностью. Электромагнитные волны обладают свойствами интерференции (опыт Герца), дифракции (алюминиевая пластинка), поляризации (сетка).
. Свойства электромагнитных волн схожи со свойствами других волновых процессов. При прохождении границы раздела двух сред частично отражаются, частично преломляются. От поверхности диэлектрика не отражаются, от металлов отражаются практически полностью. Электромагнитные волны обладают свойствами интерференции (опыт Герца), дифракции (алюминиевая пластинка), поляризации (сетка).
62. Принципы радиосвязи. Простейший радиоприемник.
Для осуществления радиосвязи необходимо обеспечить возможность излучения электромагнитных волн. Чем больше угол между пластинами конденсатора – тем более свободно ЭМ-волны распространяются в пространстве. В действительности, открытый контур состоит из катушки и длинного провода – антенны. Один конец антенны заземлен, другой – поднят над поверхностью Земли. Т.к. энергия электромагнитных волн пропорциональна четвертой степени частоты, то при колебаниях переменного тока звуковых частот ЭМ-волны практически не возникают. Поэтому используется принцип модуляции – частотной, амплитудной или фазовой. Простейший генератор модулированных колебаний представлен на рисунке. Пусть частота колебаний контура изменяется по закону![]() . Пусть частота модулируемых звуковых колебаний также изменяется как
. Пусть частота модулируемых звуковых колебаний также изменяется как ![]() , причем W<<w. Т.к. цепь содержит нелинейный элемент – транзистор – то закон Ома не выполняется, и функция напряжения выглядит как
, причем W<<w. Т.к. цепь содержит нелинейный элемент – транзистор – то закон Ома не выполняется, и функция напряжения выглядит как ![]() (а какого черта именно так???) (G – величина, обратная сопротивлению). Подставив в это выражение значения напряжений, где
(а какого черта именно так???) (G – величина, обратная сопротивлению). Подставив в это выражение значения напряжений, где ![]() , получим
, получим ![]()
![]() . Т.к. при резонансе частоты, далекие от частоты резонанса, срезаются, то из выражения для i исчезают второе, третье и пятое слагаемые, т.е.
. Т.к. при резонансе частоты, далекие от частоты резонанса, срезаются, то из выражения для i исчезают второе, третье и пятое слагаемые, т.е. ![]() .
.
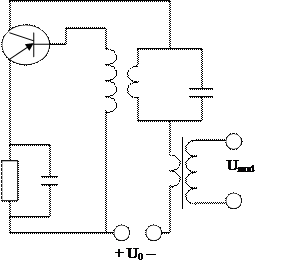 Рассмотрим простейший радиоприемник. Он состоит из антенны, колебательного контура с конденсатором переменной емкости, диода-детектора, резистора и телефона. Частота колебательного контура подбирается таким образом, чтобы она совпадала с частотой несущей, при этом амплитуда колебаний на конденсаторе становится максимальной. Это позволяет выделить нужную частоту из всех принимаемых. С контура модулированные колебания высокой частоты поступают на детектор. После прохождения детектора ток каждые полпериода заряжает конденсатор, а следующие полпериода, когда ток не проходит через диод, конденсатор разряжается через резистор. (я правильно понял???).
Рассмотрим простейший радиоприемник. Он состоит из антенны, колебательного контура с конденсатором переменной емкости, диода-детектора, резистора и телефона. Частота колебательного контура подбирается таким образом, чтобы она совпадала с частотой несущей, при этом амплитуда колебаний на конденсаторе становится максимальной. Это позволяет выделить нужную частоту из всех принимаемых. С контура модулированные колебания высокой частоты поступают на детектор. После прохождения детектора ток каждые полпериода заряжает конденсатор, а следующие полпериода, когда ток не проходит через диод, конденсатор разряжается через резистор. (я правильно понял???).
64. Аналогия между механическими и электрическими колебаниями.
Аналогии между механическими и электрическими колебаниями выглядят так:
| Координата |
| Заряд |
|
| Скорость |
| Сила тока |
|
| Ускорение |
| Скорость изменения силы тока |
|
| Масса |
| Индуктивность |
|
| Жесткость |
| Величина, обратная электроемкости |
|
| Сила |
| Напряжение |
|
| Вязкость |
| Сопротивление |
|
| Потенциальная энергия деформированной пружины |
| Энергия электрического поля конденсатора |
|
| Кинетическая энергия |
| Энергия магнитного поля катушки |
|
| Импульс |
| Поток магнитной индукции |
|
Законы колебательного движения едины для всех видов колебаний. Например, для пружинного маятника закон сохранения энергии записывается как ![]() . Продифференцировав по времени, получим
. Продифференцировав по времени, получим ![]() . Но
. Но ![]() , а
, а ![]() , поэтому
, поэтому ![]() . С математической точки зрения это уравнение идентично уравнению колебаний для колебательного контура. Поэтому его решением является
. С математической точки зрения это уравнение идентично уравнению колебаний для колебательного контура. Поэтому его решением является ![]() , где
, где ![]() .
.
Похожие работы
... закона, а на языке более уважительном и человечном. И вместо “вы обязаны”, будем говорить: “давайте попробуем”»[45]. Школьный курс по основам православной культуры является предметом культурологическим (а не религиозным), и поэтому его нужно преподавать в школе так, как необходимо преподавать математику. Так считает митрополит Смоленский и Калининградский Кирилл (Гундяев)[46]. Реализовывать эту в ...
... раза. В силу специфичности информации схемы определения количества информации, связанные с ее содержательной стороной, оказываются не универсальными. Универсальным оказывается алфавитный подход к измерению количества информации. В этом подходе сообщение, представленное в какой-либо знаковой системе, рассматривается как совокупность сообщений о том, что заданная позиция в последовательности ...
... полезно учителю при подготовке рассказа на уроке. В данной публикации сделана попытка выделить тот самый минимум, который ученику необходимо включить в свой ответ на экзамене. Примечания для учеников При ответе надо быть готовым к дополнительным вопросам об обосновании тех или иных утверждений. Например, каковы максимальное и минимальное значения 8-битного целого числа со знаком и почему их ...
... список или выбрать из 2-3 текстов наиболее интересные места. Таким образом, мы рассмотрели общие положения по созданию и проведению элективных курсов, которые будут учтены при разработке элективного курса по алгебре для 9 класса «Квадратные уравнения и неравенства с параметром». Глава II. Методика проведения элективного курса «Квадратные уравнения и неравенства с параметром» 1.1. Общие ...
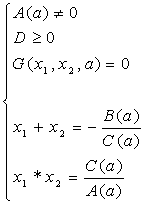
0 комментариев