НВЧ властивості плівок ВТНП
Залишковий поверхневий НВЧ опiр в надпровіднику
Поведінка надпровідників в зовнішніх магнітних полях. Надпровідники другого роду
Поведінка тонких плівок ВТНП у магнітному полі. Модель Коффі - Клема
Методика вимірювання поверхневого імпедансу і аналіз вимог до вимірювальних резонаторів
Атестація плівок по НВЧ втратам
Опис експерементальної установки
Навигация
Поведінка надпровідників в зовнішніх магнітних полях. Надпровідники другого роду
Высокотемпературная сверхпроводимость
47733
знака
9
таблиц
18
изображений
1.5. Поведінка надпровідників в зовнішніх магнітних полях. Надпровідники другого роду.
Магнітні властивості надпровідників характеризуються двома параметрами: глибиною проникнення L слабкого постійного поля в внутрішні області надпровідника, яку ввели Лондони і довжиною когерентності x0, введену Піппардом.
В квазімікроскопічній теорії Гінзбурга -Ландау був введений безрозмірний параметр c=L/x0. Для чистих металів ( олова, алюмінія, ртуті та інші ) значення c мале. Наприклад, для ртуті c=0,16. Тому в роботі Гінзбурга - Ландау розглядались тільки випадки, коли 
.
В 1957 році А.А. Абрикосов показав, що з теорії Гінзбурга - Ландау витікає можливість існування двох груп надпровідників. До першої відносяться надпровідники із значеннями 
, котрі були названі надпровідниками першого роду. В них в зовнішньому полі Н<Hc середнє магнітне поле всередені зразка 
. При рості зовнішнього магнітного поля відбувається скачкоподібне ( не більше одного - двох гаусів ) знищення надпровідності.
До другої групи відносяться надпровідники, у яких в де-якому інтервалі магнітних полів відбувається часткове проникнення магнітного поля в масивний надпровідник. До цієї групи відносяться надпровідники з значеннями 
. Це сплави, наприклад свинець - вісмут, свинець - талій, ртуть - кадмій та деякі нечисті метали, у яких довжина когерентності x0 мала.
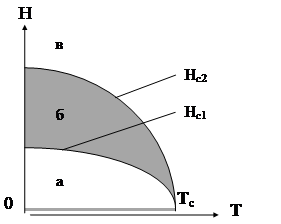
Надпровідники із значеннями називаються надпровідниками другого роду. Вони характеризуються двома критичними полями Нс1 та ( рис.1.5.1) . В них зовнішнє поле не проника всередену масивного зразка до Н= Нс1. При збільшенні зовнішнього поля від Нс1 до Нс2 поле частково проникає всередену зразка так, що індукція поля зростає і при Нс2 наближається до значення, характерного для нормального метала. Електричний опір зразка при наближенні до поля Нс2 залишається рівним нулю.
В масивних надпровідниках другого роду верхнє критичне поле пов’язане з нижнім співвідношнням
. (1.5.1)
В цих надпровідниках переходи Нс1 і Нс2 є фазовими переходами другого роду. Вони не супроводжуються виділенням теплоти, але для них є характерним стрибок теплоємності.
При намагніченні довгого циліндра в полі, меншим критичного значення Нс1 і перпендикулярним осі циліндра, середнє поле індукції 
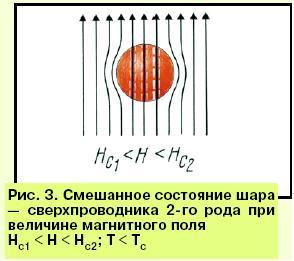
всередені зразка рівне нулю. При зовнішньому полі Н, яке задовільняє нерівність Hc1<H<Hc2, всередені надпровідника появляється поле , менше Н, і одночасно існують нормальна і надпровідна фази. Такий стан Абрикосов назвав змішаним. Ще цей стан називають фазою Шубнікова [ 16 ], який спостерігав це явище експерементально. При зовнішньому полі Н³ Hc2 середнє поле всередені зразка зрівнюється з зовнішнім полем Н і надпровідність в об’ємі зникає.
 | |||
| |||
Рис.1.5.1. Фазова діаграма надпровідника ІІ роду.
Таким чином, надпровідники другого роду при значеннях зовнішнього магнітного поля Н, які лежать в інтервалі Hc1<H<Hc2 , не є ідеальними діамагнетиками. При таких значеннях поля спарювання електронів відсутнє вздовж деяких ліній, паралельних зовнішньому магнітному полю.
Посліловну феноменологічну теорію надпровідності другого роду на основі квазімікроскопічної теорії Гінзбурга - Ландау розвинув в 1957 році фізик - теоретик А.А. Абрикосов для значень параметра . В цьому випадку справедливе лондоновське локальне наближення. В магнітних полях, набагато менших Hc2, хвильова функція надпровідного стану мала. Встановлено, що при полях Н, більших Hc1 і маловідмінних від Hc2, магнітний потік проникає всередену зразка у вигляді регулярної структури трубок, кожна із яких несе квант магнітного потоку
гс×см2.
(1.5.2)
На переферії кожної окремої трубки протікає вихрь надструму, який зжимає в центральній області магнітний поток, рівний одному кванту потоку Ф0. На існування кванта магнітного потоку вперше звернув увагу Ф. Лондон в 1950 році. Без врахування куперовського спарювання його квант в два рази перевищував Ф0.
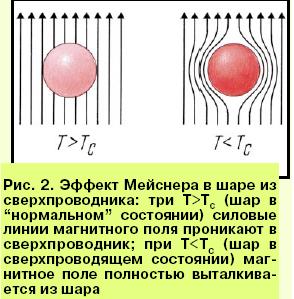
Слабкі магнітні поля ( <Hc1 ) не проникають всередену зразка, тобто існує ефект Мейснера. В цьому випадку власна енергія вихря перевищує магнітну енергію, яка виникає при проникненні одного кванта магнітного потоку всередену надпровідника. Ця енергія вирювнюється в полі Н=Нс1. При Н>Нс1 магнітні вихрі починають проникати в надпровідник, розташовуючись паралельно зовнішнньому магнітному полю. Розрахунки показують [ 17 ], що нитки починають утворюватись, коли напруженність поля Н>Нс1 досягає значення
.
(1.5.3)
При дальшому збільшенні поля проникання магнітного потоку всередену зразка відбувається у вигляді віддалених одної від одної вихрьових ниток, створюючих структуру типу гратки з дуже великим періодом. В полях, близьких Нс2 , в вузлах решітки поле Y2 рівне нулю, а магнітне поле має максимальне значення і практично відсутнє в проміжках між нитками ( надпровідна фаза ).
При достатньому віддалені ниток однієї від одної їх можна вважати незалежними і розглядати
одну окрему нитку. По структурі вихрьова нитка складається в основному з двох областей: центральної циліндричної області з діаметром, приблизно рівним довжині когерентності x0. В цій області густина надпровідних електронів 
виростає від нуля до одиниці. Цю внутрішню область охоплює зовнішня циліндрична область, з радіусом порядка глибини проникнення L, магнітного поля. В цій області циркулюють незатухаючі струми, необхідні для створення одного кванту Ф0 магнітного потоку. Структура ізольованої вихрьової нитки показана на рис.1.5.2.
 | |||||||
 |
|  | |||||
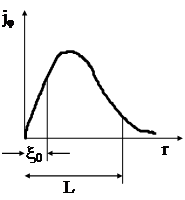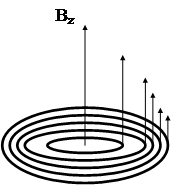Рис.1.5.2. Ізольована вихрьова нитка Абрикосова: Вz-лінії магнітного поля; jj-замкнуті лінії надпровідного струму.
Енергія одиниці довжини нитки визначається виразом
(1.5.4)
Випливає, що без врахування взаємодії ниток енергія N вихрьових ниток, які перетинають одиницю площі, рівна NeS. Вільна енергія надпровідника визначається виразом
.
(1.5.5)
При слабкому зовнішньому полі вільна енергія F додатня і утворення вихрів невигідно, але при H³HФ, де HФ визначено рівністю (1.5.3), вона стає від’ємною і утворення вихрів вигідно.
Якщо в нульовому магнітному полі Fn - густина енергії нормального стану, а Fs0 - густина енергії надпровідного змішаного стану надпровідника другого роду, їх різниця визначає так зване критичне термомагнітне поле за допомогою рівності:
. (1.5.6)
Для надпровідників першого роду це співвідношення визначає істинне критичне поле Нст=Нс. Для надпровідників другого роду значення Нст характеризує тільки допоміжну величину.
Умова термодинамічної рівноваги змішаного стану надпровідника другого роду зводиться до вимоги, щоб поле в його нормальній фазі було рівним критичному термодинамічному полю Нст. Це поле виражається через параметри L, x-0 і Ф0 рівністю
(1.5.7)
Друге критичне поле Нс2 надпровідника другого роду пов’язане з полем Нст співвідношенням
(1.5.8)
Для матеріалів з довжиною когерентності x-0 надпровідність зберігається до дуже великих значень поля Нс2. Наприклад, в сплаві V3Ga при Т=0 критичне поле Нс2=3×105 гс.
В полях Н, які неперевищують друге критичне поле, магнітне поле не витісняється з циліндричного зразка. Однак, в області полів Н, які задовільняють нерівності Hc1<H<Hc2, на поверхні циліндра зберігається надпровідність в тонкому шарі ( ~ 103 А ). Поле Нс3 називається третім критичним полем. За звичай Нс3=1,69 Hc2. По зовнішній і внутрішній поверхні цього надпровідника протікають в протилежних напрямках надпровідні струми.
При значеннях магнітного поля, близьких Hc2, в однорідному надпровіднику другого роду змішаний стан характеризується правильною двохвимірною граткою Абрикосова. При збільшенні зовнішнього магнітного поля період гратки зменшується. При наближенні значення Н до Hc2 період досягає величини порядку x-0 ( вихрьові нитки доторкуються одна до одної ), відбувається фазовий перехід другого роду із змішаного стану в нормальний.
Якщо надпровідник ІІ роду знаходиться в змішаному стані і в напрямку, перпендикулярному вихрям, протікає транспортний струм, створений зовнішнім джерелом, то на вихрі діє сила Лоренца. Ця сила перпендикулярна струму і магнітному полю вихря. Під дією сили Лоренца магнітні вихрі переміщаються впоперек транспортному струмові (рис .1.5.3 ).
 |  |  |
Рис. 1.5.3. Рух магнітної вихрьової лінії при наявності транспортного струму: F - сила Лоренца.
Рух магнітного поля вихря створює електричне поле, направлене вздовж вихря, яке викликає гальмування електронів. Виникає електричний опір, який називається резистивним.
В повністю однорідному зразку навіть при досить малій силі Лоренца переміщення вихрів пов’язано з втратою енергіїі зникненням надпровідності. Таким чином, для абсолютно чистого зразка критичний струм, який руйнує надпровідність, рівний нулю.
В неоднорідних надпровідниках ІІ роду завжди є дефекти різного роду ( границі зерен, пори, дислокації та ін. ). На цих неоднорідностях вихрі закріплюються. Явище закріплення визрів називають пінінгом. Надпровідники з сильним пінінгом називаються жорсткими.
При наявності пінінга необхідний кінечний транспортний струм для зриву і руху вихрів. Густина струму, при котрій починається зрив вихрів від центра пінінга, називається критичною густиною струму.
Різні ненадпровідні включення з розмірами порядку кореляційної довжини x0 є ефективними центрами пінінга. Вони характеризуються «силою пінінга»,рівній силі Лоренца, при котрій починається відрив магнітного вихря. Спеціальною механічною і термообробкою, а також включеннями ненадпровідних домішок створюються жорсткі надпровідникиз багаточисленними центрами пінінга.
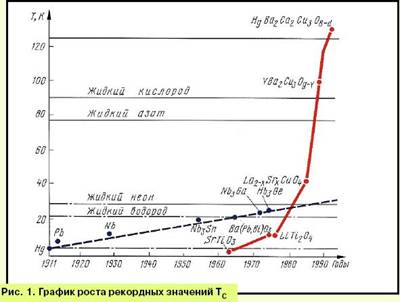
Якщо критичні поля чистих металів не перевищували 0,2 Тл, то створені на початку 60-х років жорсткі надпровідники, утворені із сплавів Nb-Ti, Nb-Zr, Nb-Sn та інші., дозволили виготовляти невеликі соленоїди з критичними полями до 10 Тл при високих густинах транспортного критичного струму - порядку 105-106 А/см2. Ці високі значення полів і струмів були отримані при спеціалній термомеханічній обробці, яка забеспечує створення великого числа центрів пінінга.
Похожие работы
... реакторов. Несомненно, что использование сверхпроводимости будет в ближайшие годы расширяться - взять хотя бы квантовые компьютеры, в которых без сверхпроводимости не обойтись. Однако до сих пор природа необычной высокотемпературной сверхпроводимости остается для ученых загадкой. В обычных сверхпроводниках сверхпроводимость характеризуется параметром порядка, который может зависеть только от ...
... (за исключением тонкого поверхностного слоя толщиной 100...1000 ангстрем) оно всегда равно нулю. Именно эти два свойства - бесконечная проводимость и идеальный диамагнетизм - являются главными характеристиками сверхпроводимости. Исследования открыли ещё один важный эффект. Если увеличивать напряженность магнитного поля, то при некоторой величине его Н=Нс, называемой "критическое магнитное поле", ...
... фундаментальных исследований может, как правило, претендовать только на статус любителя по части их практических приложений. Тем не менее возможно указать на некоторые перспективы: -когда рассматривался как ВТСП карбин то мечты о его высокотемпературной сверхпроводимости можно было считать беспочвенными: уж очень сходен карбин по своей структуре с тем полимером , который предлагал Литлл и который ...
... невозможно. Практического применения высокотемпературные сверхпроводники на сегодняшний день не находят по причине их крайней дороговизны и хрупкости, однако разработки в этом направлении продолжаются. Сверхпроводящие материалы Явление сверхпроводимости при криогенных температурах достаточно широко распространено в природе. Сверхпроводимостью обладают 26 металлов. Большинство из них ...
0 комментариев