НВЧ властивості плівок ВТНП
Залишковий поверхневий НВЧ опiр в надпровіднику
Поведінка надпровідників в зовнішніх магнітних полях. Надпровідники другого роду
Поведінка тонких плівок ВТНП у магнітному полі. Модель Коффі - Клема
Методика вимірювання поверхневого імпедансу і аналіз вимог до вимірювальних резонаторів
Атестація плівок по НВЧ втратам
Опис експерементальної установки
Навигация
Поведінка тонких плівок ВТНП у магнітному полі. Модель Коффі - Клема
Высокотемпературная сверхпроводимость
47733
знака
9
таблиц
18
изображений
1.6. Поведінка тонких плівок ВТНП у магнітному полі. Модель Коффі - Клема.
Перейдемо до розгляду поведiнки надпровiдника ІІ-го роду, який знаходиться у змiшаному станi на НВЧ. На iзольований флюксоїд, пронизуючий ВТНП, будуть дiяти такi сили: якщо по флюксоїду тече транспортний струм густиною j=j0e-iwt, то на одиницю довжини флюксоїда з боку магнiтних складових НВЧ - поля, перпендикулярних струму, буде дiяти сила Лоренца :
, (1.6.1)
де 
— повний магнiтний потiк, який пронизує флюкоїд,
аf — радiус флюксоїда.
Сила пiнiнгу:
, (1.6.2)
де 
— стала пiнiнгу на одиницю довжини флюксоїда,
хf — вiдхилення флюксоїда вiд положення рiвноваги.
Сила пiнiнгу обумовлена тим, що вихорi можуть бути закрiпленi (запiнiнгованi) на iснуючих в ВТНП дефектах: границi зерен, дислокації, пори i т.п., до того, поки сила Лоренца не перевищить силу пiнiнгу, в результатi чого стане можливим коливальний рух вихорiв навколо центрiв закрiплення.
В процесi руху вихорiв на них буде дiяти сила в'язкостi:
, (1.6.3)
де hf — коефiцieнт в'язкостi, який дорiвнює:
, (1.6.4)
де rn — питомий опiр ВТНП у нормальному станi H0=HC2 при T=0. Якщо позначити масу флюксоїда на одиницю довжини mf , то рiвняння руху пiд дiєю перерахованих вище сил, можна записати в такому виглядi:
, (1.6.5)
Рiшення цього рiвняння запишеться в такому виглядi:
,
де
; 
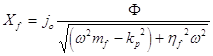З урахуванням цього рiшення, можна знайти опiр осцилюючого флюксоїда:
,
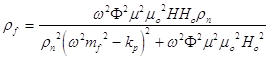(1.6.6)
Для того, щоб дослiдити залежнiсть вiд рiзних параметрiв у широкому дiапазонi їх змiни необхiдно знати точний вираз для маси флюксоїда на одиницю його довжини:
, (1.6.7)
де ax — кут Холла, тобто кут мiж струмом та магнiтним полем,
ne i me — густина та маса електронiв.
Вираз для поверхневого iмпедансу ВТНП плiвки можна одержати припускаючи, що ВТНП плiвка, яка знаходиться у надпровiдному станi на НВЧ, виконує роль, еквiвалентну лiнії передачi в електроницi НВЧ з хвильовим опором ZS , а пiдкладинка має хвильовий опiр 
, де e - дiелектрична проникливiсть пiдкладки, яка навантажена на цю лiнiю передачi на вiдстанi h (h - товщина ВТНП плiвки). Таким чином, можна скористатися вiдомим виразом для визначення опору в довiльнiй точцi цiєї лiнії [ 18 ]:
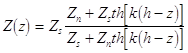, (1.6.8)
де k — стала розповсюдження електромагнiтної хвилi.
Вважаючи, що глибина проникнення електромагнiтної хвилi у надпровiдник d<<h (тобто h>>z) та враховуючи, що k=1/dk , вираз (1.5.8) матиме вигляд :
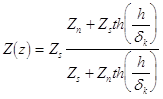, (1.6.9)
де dk — комплексна глибина проникнення електромагнiтного поля в надпровiдник, згiдно моделi Коффi-Клема [8] :
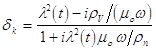, (1.6.10)
де l(t) — глибина проникнення постiйного магнiтного поля :
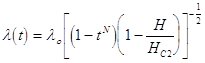, (1.6.11)
де 1£N£4.
Навiть кращi реальнi ВТНП плiвки, якi є епiтаксiальними, мають велику кiлькiсть дефектiв, що роблять плiвки практично полiкристалiчними i складаються з окремих зерен, з’єднаних мiж собою слабкими зв'язками. Для таких плiвок l0 вже не звичайна лондонiвська глибина проникнення lL , а представляє собою складну функцiю форми та розмiрiв зерен та властивостей слабких зв'язкiв. На мiкрохвильовi властивостi найбiльше впливають плоскi дефекти, що розмiщенi перпендикулярно напрямку розповсюдження струму.
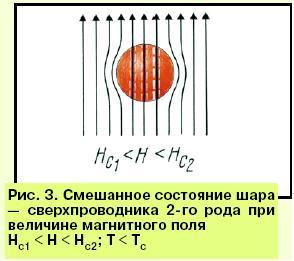
Iснують двi категорії дефектiв та вiдповiдаючих їм слабких зв'язкiв, якi визначають НВЧ властивостi ВТНП плiвок: плоскi двовимiрнi внутригранульнi зв'язки, обумовленi двiйниками, бiльше i малокутовими границями з лiнiйними розмiрами вздовж струму d<x та крупномасштабнi мiжгранульнi слабкi зв'язки. В епiтаксiальних ВТНП плiвках першi практично вiдсутнi, а для останнiх основнє значення мають такi дефекти, як великокутовi границi, де величина поверхневого iмпедансу тут пропорцiйна об’ємнiй частцi високорозорiєнтованих дiлянок плiвки. Залежнiсть вiд поля глибини проникнення може бути найбiльш суттєва для джозефсонiвських середовищ, якими й являються реальнi ВТНП.
Для мiжгранульних зв'язкiв НC2=НC2j~100Е для внутригранульних Нс>104E. Залежнiсть поверхневого iмпедансу ВТНП плiвок вiд постiйного магнiтного поля з урахуванням руху вихорiв магнiтного потоку, можна описати, згiдно моделi Коффi-Клема, спiввiдношенням виду :
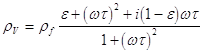, (1.6.12)
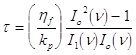
З (1.6.6) при 
, (1.6.13)
де Ip(n) — модифiкована функцiя Бесселя першого роду, р-го порядку
n=U/2kБТ, де U — висота потенцiального барьеру для вихорiв магнiтного потоку. Вважаємо, що U, kp — є деякi ефективнi величини, однаковi для усiх вихорiв.
Відносне значення поверхневого опору в магнітному полі в наближенні l2(t)<<2rn/m0w для тонкої надпровідникової плівки згідно (1.6.8)-(1.6.12) має вигляд:
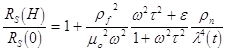, (1.6.14)
Розділ ІІ. Методична частина.
Похожие работы
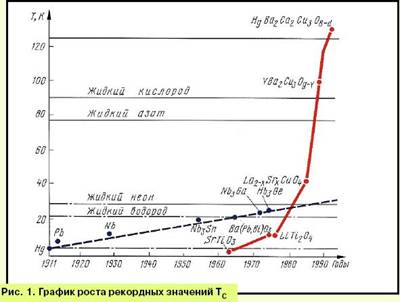
... реакторов. Несомненно, что использование сверхпроводимости будет в ближайшие годы расширяться - взять хотя бы квантовые компьютеры, в которых без сверхпроводимости не обойтись. Однако до сих пор природа необычной высокотемпературной сверхпроводимости остается для ученых загадкой. В обычных сверхпроводниках сверхпроводимость характеризуется параметром порядка, который может зависеть только от ...
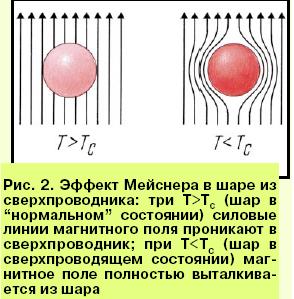
... (за исключением тонкого поверхностного слоя толщиной 100...1000 ангстрем) оно всегда равно нулю. Именно эти два свойства - бесконечная проводимость и идеальный диамагнетизм - являются главными характеристиками сверхпроводимости. Исследования открыли ещё один важный эффект. Если увеличивать напряженность магнитного поля, то при некоторой величине его Н=Нс, называемой "критическое магнитное поле", ...
... фундаментальных исследований может, как правило, претендовать только на статус любителя по части их практических приложений. Тем не менее возможно указать на некоторые перспективы: -когда рассматривался как ВТСП карбин то мечты о его высокотемпературной сверхпроводимости можно было считать беспочвенными: уж очень сходен карбин по своей структуре с тем полимером , который предлагал Литлл и который ...
... невозможно. Практического применения высокотемпературные сверхпроводники на сегодняшний день не находят по причине их крайней дороговизны и хрупкости, однако разработки в этом направлении продолжаются. Сверхпроводящие материалы Явление сверхпроводимости при криогенных температурах достаточно широко распространено в природе. Сверхпроводимостью обладают 26 металлов. Большинство из них ...
0 комментариев