Навигация
В соответствии с заданной ВАХ нелинейный резистор на участке 1-2 заменяем линейным резистором с сопротивлением
1. В соответствии с заданной ВАХ нелинейный резистор на участке 1-2 заменяем линейным резистором с сопротивлением
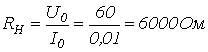 ,
,
на
участке 2-3-источником
тока с током
![]() и
на участке
4-1-источником
тока с током
и
на участке
4-1-источником
тока с током
![]() .
.
2. На основании данной эквивалентной замены для тока на участке 1-2 ВАХ можно записать:
|
| (1) |
откуда
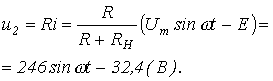
При движении изображающей точки по участку 2-3 ВАХ имеем
![]() ,
,
при движении по участку 1-4 ВАХ-
![]() .
.
3. Определяем интервалы движения изображающей точки по отдельным участкам ВАХ. Для точки излома 1 на основании (1) справедливо уравнение
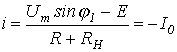
или
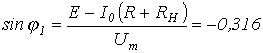 .
.
Отсюда
получаем два
значения мгновенной
фазы питающего
напряжения
на одном периоде,
соответствующих
точке 1: ![]() .
Первое значение
определяет
переход изображающей
точки с участка
4-1 на участок
1-2, второе – с
участка 2-1 на
участок 1-4.
.
Первое значение
определяет
переход изображающей
точки с участка
4-1 на участок
1-2, второе – с
участка 2-1 на
участок 1-4.
Аналогично записываем для точки 2 излома ВАХ
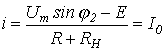
или
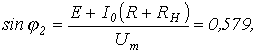
откуда
![]() (значение,
соответствующее
переходу с
участка 1-2 на
участок 2-3) и
(значение,
соответствующее
переходу с
участка 1-2 на
участок 2-3) и
![]() (значение,
соответствующее
переходу с
участка 3-2 на
участок 2-1).
(значение,
соответствующее
переходу с
участка 3-2 на
участок 2-1).
Таким образом, получаем для одного периода питающего напряжения
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
.
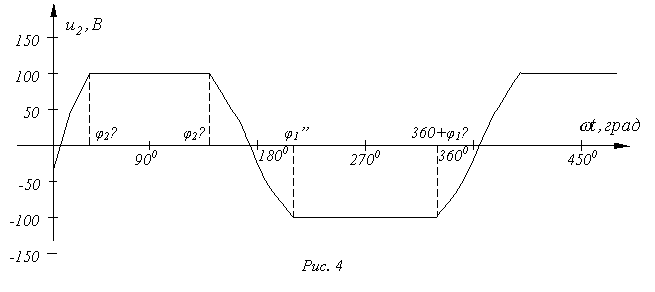
В соответствии с периодичностью синусоидальной функции данные решения повторяются через 360°n.
На рис. 4 представлен график зависимости искомой величины.
Метод гармонического баланса
Применение аналитического выражения для аппроксимации характеристики нелинейного элемента позволяет наименее трудоемко провести расчет, когда закон изменения во времени одной из переменных, определяющих работу нелинейного элемента (ток или напряжение для резистора, потокосцепление или ток для катушки индуктивности, заряд или напряжение для конденсатора), задан или вытекает из предварительного анализа физических условий протекания процесса, что имело место при решении предыдущих задач данного раздела. Если такая определенность отсутствует, то задачу в общем случае можно решить только приближенно. Одним из таких методов, наиболее широко применимым на практике, является метод гармонического баланса.
Метод основан на разложении периодических функций в ряд Фурье. В общем случае искомые переменные в нелинейной электрической цепи несинусоидальны и содержат бесконечный спектр гармоник. Ожидаемое решение можно представить в виде суммы основной и нескольких высших гармоник, у которых неизвестными являются амплитуды и начальные фазы. Подставляя эту сумму в нелинейное дифференциальное уравнение, записанное для искомой величины, и приравнивая в полученном выражении коэффициенты перед гармониками (синусоидальными и косинусоидальными функциями) одинаковых частот в его левой и правой частях, приходим к системе из 2n алгебраических уравнений, где n-количество учтенных гармоник. Необходимо отметить, что точное решение требует учета бесконечного числа гармоник, что невозможно осуществить практически. В результате ограничения числа рассматриваемых гармоник точный баланс нарушается, и решение становится приближенным.
Методика расчета нелинейной цепи данным способом включает в себя в общем случае следующие основные этапы:
1. Записываются уравнения состояния цепи для мгновенных значений.
2. Выбирается выражение аналитической аппроксимации заданной нелинейности.
3. На основе
предварительного
анализа цепи
и нелинейной
характеристики
задается выражение
искомой величины
в виде конечного
ряда гармоник
с неизвестными
на этом этапе
амплитудами
![]() и
начальными
фазами
и
начальными
фазами ![]() .
.
4. Осуществляется подстановка функций, определенных в пунктах 2 и 3, в уравнения состояния с последующей реализацией необходимых тригонометрических преобразований для выделения синусных и косинусных составляющих гармоник.
5. Производится
группировка
членов в полученных
уравнениях
по отдельным
гармоникам,
и на основании
приравнивания
коэффициентов
при однопорядковых
гармониках
в их левых и
правых частях
(в отдельности
для синусных
и косинусных
составляющих)
записывается
система нелинейных
алгебраических
(или трансцендентных)
уравнений
относительно
искомых амплитуд
![]() и
начальных фаз
и
начальных фаз
![]() функции
разложения
определяемой
величины.
функции
разложения
определяемой
величины.
6. Осуществляется
решение (в общем
случае численными
методами на
ЭВМ) полученной
системы уравнений
относительно
![]() и
и
![]() .
.
Частным случаем метода гармонического баланса является метод расчета по первым гармоникам несинусоидальных величин (метод гармонической линеаризации), когда высшими гармониками искомых переменных, а также входных воздействий пренебрегают. При анализе используется характеристика нелинейного элемента по первым гармоникам, для получения которой в аналитическое выражение нелинейной характеристики для мгновенных значений подставляется первая гармоника одной из двух переменных, определяющих эту характеристику, и находится нелинейная связь между амплитудами первых гармоник этих переменных. Этапы расчета соответствуют изложенным для метода гармонического баланса. При этом, в силу того, что конечная система нелинейных уравнений имеет второй порядок, в ряде случаев появляется возможность их аналитического решения. Кроме того, поскольку рассматриваются только первые гармоники несинусоидальных величин, при расчете можно использовать символический метод.
Пусть,
например, в
цепи, питаемой
от источника
синусоидального
напряжения
![]() и
состоящей из
последовательно
соединенных
линейного
резистора
и
состоящей из
последовательно
соединенных
линейного
резистора ![]() и
нелинейной
катушки, вебер-амперная
характеристика
которой задана
аппроксимацией
вида
и
нелинейной
катушки, вебер-амперная
характеристика
которой задана
аппроксимацией
вида ![]() ,
необходимо
определить
первую гармонику
тока, задаваемую
выражением
,
необходимо
определить
первую гармонику
тока, задаваемую
выражением
![]() ,
где
,
где ![]() и
и
![]() -
неизвестные
(искомые величины).
-
неизвестные
(искомые величины).
Для
решения определяем
аналитическое
выражение
характеристики
![]() для
первых гармоник:
для
первых гармоник:
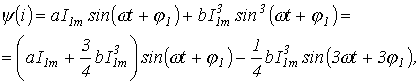
откуда
|
| (2) |
После подстановки выражения тока и соотношения (2) в уравнение состояния цепи
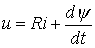
получаем
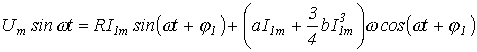
или
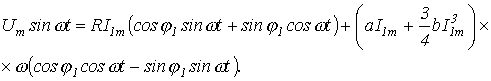
На основании последнего получаем систему уравнений
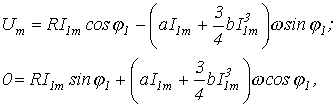
из
которых находим
искомые параметры
![]() и
и
![]() .
.
Литература
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
Каплянский А.Е. и др. Теоретические основы электротехники. Изд. 2-е. Учеб. пособие для электротехнических и энергетических специальностей вузов. –М.: Высш. шк., 1972. –448 с.
Контрольные вопросы и задачи
В чем заключается сущность метода кусочно-линейной аппроксимации?
На чем основан метод гармонического баланса?
Сформулируйте основные этапы расчета нелинейной цепи методом гармонического баланса.
В чем состоит сущность метода расчета по первым гармоническим?
Как определяется характеристика нелинейного элемента для первых гармоник?
Резистивная нагрузка подключена к источнику синусоидального напряжения через последовательно включенный с ней диод. Считая ВАХ диода идеальной, определить коэффициент мощности. Обоснуйте физически полученный результат.
Ответ:
![]() .
.
Последовательно соединенные линейный конденсатор с ![]() и нелинейная катушка, вебер-амперная характеристика которой аппроксимирована выражением
и нелинейная катушка, вебер-амперная характеристика которой аппроксимирована выражением ![]() , где
, где ![]() , питаются от источника синусоидального напряжения
, питаются от источника синусоидального напряжения ![]() . Ограничившись рассмотрением первой и третьей гармонических, определить потокосцепление.
. Ограничившись рассмотрением первой и третьей гармонических, определить потокосцепление.
Ответ:
![]() .
.
Лекция N 37
Метод эквивалентных синусоид (метод расчета по действующим значениям)Сущность метода эквивалентных синусоид была изложена в лекции №35 при рассмотрении его графической реализации. При аналитическом варианте применения метода отсутствует основной этап графических построений, в частности векторных диаграмм, который заменяется соответствующими вычислениями с использованием аналитических соотношений для комплексов эквивалентных синусоидальных величин.
Графический вариант применения метода эквивалентных синусоид характеризуется, в первую очередь для относительно простых схем, большей наглядностью. В то же время при аналитическом подходе повышается точность расчетов за счет устранения погрешностей, связанных с графическими построениями.
 Переход
к эквивалентным
синусоидам
в сочетании
с символическим
методом позволяет
составлять
эквивалентные
схемы замещения
с эквивалентными
параметрами
Переход
к эквивалентным
синусоидам
в сочетании
с символическим
методом позволяет
составлять
эквивалентные
схемы замещения
с эквивалентными
параметрами
![]() и
и
![]() .
Трудности
анализа и расчета
заключаются
в том, что значения
этих параметров
зависят от
искомых напряжений,
токов и потоков,
т. е. заранее
не известны.
.
Трудности
анализа и расчета
заключаются
в том, что значения
этих параметров
зависят от
искомых напряжений,
токов и потоков,
т. е. заранее
не известны.
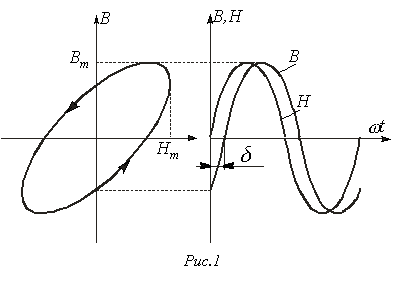
Переход
к эквивалентным
синусоидам
соответствует
замене реальных
петель гистерезиса
![]()
![]() или
или
![]()
![]() эквивалентными
эллипсами. На
рис. 1 представлен
эквивалентный
эллипс, заменяющий
реальную кривую
эквивалентными
эллипсами. На
рис. 1 представлен
эквивалентный
эллипс, заменяющий
реальную кривую
![]() ,
которому
соответствуют
параметрические
уравнения,
определяемые
синусоидальными
функциями
,
которому
соответствуют
параметрические
уравнения,
определяемые
синусоидальными
функциями
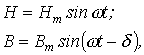
где
![]() -угол
потерь, определяющий
мощность потерь
в единице объема
ферромагнетика
за один цикл
перемагничивания
-угол
потерь, определяющий
мощность потерь
в единице объема
ферромагнетика
за один цикл
перемагничивания
![]() .
.
При
переменных
токах потери
в стали сердечника
определяются
не только
гистерезисом,
но и вихревыми
токами, вызываемыми
переменным потоком. Таким
образом, динамическая
петля гистерезиса
шире статической
и отличается
от последней
по форме. Отметим,
что для уменьшения
потерь от вихревых
токов сердечник
набирают из
изолированных
тонких листов
(при частоте
![]() Гц
их толщина
Гц
их толщина
![]() мм),
выполненных
из сталей со
специальными
присадками,
снижающими
проводимость.
мм),
выполненных
из сталей со
специальными
присадками,
снижающими
проводимость.
При пренебрежении неравномерностью распределения магнитной индукции по сечению мощность потерь от вихревых токов определяется соотношением
![]() ,
,
где
![]() -
эмпирический
коэффициент,
определяемый
сортом стали
и размером
листов; G – масса
сердечника.
-
эмпирический
коэффициент,
определяемый
сортом стали
и размером
листов; G – масса
сердечника.
В свою очередь мощность потерь от гистерезиса
![]() ,
,
где
n=1,8…2,2 (часто в первом
приближении
принимается
n=2); ![]() -
эмпирический
коэффициент,
зависящий от
сорта стали.
-
эмпирический
коэффициент,
зависящий от
сорта стали.
Полные
потери в стали
![]() ,
помимо указанных,
определяются
также дополнительными
,
помимо указанных,
определяются
также дополнительными
![]() ,
связанными
с магнитной
вязкостью
материала, т.е.
,
связанными
с магнитной
вязкостью
материала, т.е.
![]() .
.
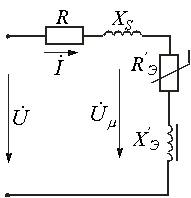
Для определения параметров эквивалентной синусоиды тока: его действующего значения и угла потерь (фазового сдвига относительно магнитного потока) - удобно пользоваться соотношением для мощности потерь в стали
![]()
и намагничивающей мощности
![]()
где
![]() –
напряжение,
приложенное
к нелинейной
катушке индуктивности
с числом витков
–
напряжение,
приложенное
к нелинейной
катушке индуктивности
с числом витков
![]() и
площадью сечения
сердечника
и
площадью сечения
сердечника
![]() ;
; ![]() -соответственно
удельные (на
единицу массы
сердечника)
потери в стали
и намагничивающая
мощность. Значения
-соответственно
удельные (на
единицу массы
сердечника)
потери в стали
и намагничивающая
мощность. Значения
![]() и
и
![]() берутся
из экспериментальных
характеристик
берутся
из экспериментальных
характеристик
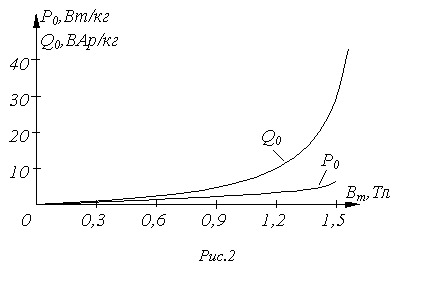
![]() и
и
![]() ,
выражающих
зависимости
этих величин
от амплитуды
индукции (см.
в качестве
примера кривые
на рис. 2) в режиме
синусоидальной
индукции.
,
выражающих
зависимости
этих величин
от амплитуды
индукции (см.
в качестве
примера кривые
на рис. 2) в режиме
синусоидальной
индукции.
Переход
к эквивалентным
синусоидам
и соответственно
к эквивалентному
эллипсу, заменяющему
реальную кривую
зависимости
![]() ,
позволяет
ввести в рассмотрение
относительную
комплексную
магнитную
проницаемость
,
позволяет
ввести в рассмотрение
относительную
комплексную
магнитную
проницаемость
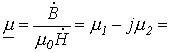
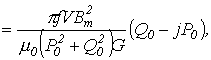
где
![]() -
объем стали
сердечника
длиной
-
объем стали
сердечника
длиной ![]() и
сечением
и
сечением ![]() ,
,
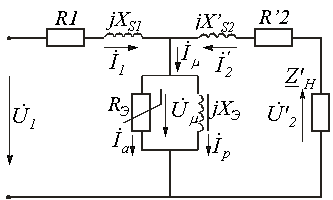
и комплексное магнитное сопротивление
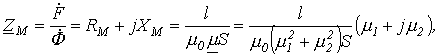
являющееся
аналогом магнитному
сопротивлению
![]() в
нелинейных
цепях при постоянных
магнитных
потоках.
в
нелинейных
цепях при постоянных
магнитных
потоках.
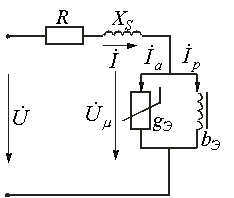
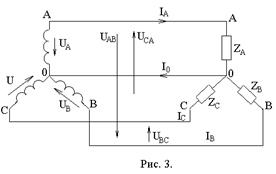
Катушка с ферромагнитным сердечником
Н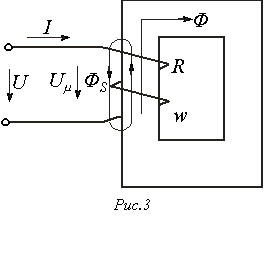 елинейная
катушка индуктивности
изображена
на рис. 3. Здесь
R-активное
сопротивление
обмотки с числом
витков w; Ф-основной
поток, замыкающийся
по сердечнику;
елинейная
катушка индуктивности
изображена
на рис. 3. Здесь
R-активное
сопротивление
обмотки с числом
витков w; Ф-основной
поток, замыкающийся
по сердечнику;
![]() -поток
рассеяния,
которому
соответствует
индуктивность
рассеяния
-поток
рассеяния,
которому
соответствует
индуктивность
рассеяния ![]() и
индуктивное
сопротивление
рассеяния
и
индуктивное
сопротивление
рассеяния ![]() .
.
Различают параллельную и последовательную схемы замещения катушки с ферромагнитным сердечником. Эти схемы, а также соответствующие им соотношения и векторные диаграммы приведены в табл. 1.
Таблица 1. Схемы замещения, уравнения и векторные диаграммы для катушки c ферромагнитным сердечником
| Схема замещения | Уравнения и соотношения для параметров | Векторная диаграмма | ||||
| Параллельная Последовательная
|
где где
|
|
Примечание.
1. Если сердечник
содержит воздушный
зазор величиной
![]() ,
в схему замещения
параллельно
ветви, содержащей
нелинейную
катушку с
проводимостью
,
в схему замещения
параллельно
ветви, содержащей
нелинейную
катушку с
проводимостью
![]() ,
включается
дополнительная
линейная катушка
индуктивности
с сопротивлением
,
включается
дополнительная
линейная катушка
индуктивности
с сопротивлением
![]()
2.
При пренебрежении
активным
сопротивлением
обмотки и потоком
рассеяния связь
между эквивалентным
электрическим
сопротивлением
![]() катушки
и комплексным
магнитным
сопротивлением
катушки
и комплексным
магнитным
сопротивлением
![]() сердечника
определяется
соотношением
сердечника
определяется
соотношением
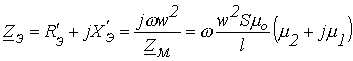
или
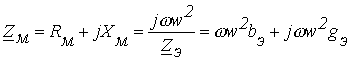 .
.
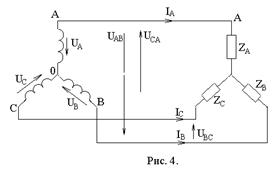
Трансформатор с ферромагнитным сердечником
Т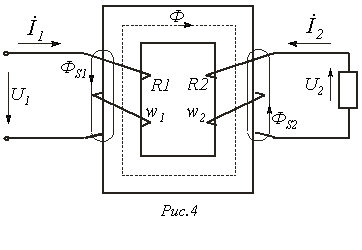 рансформатор
с ферромагнитным
сердечником
изображен на
рис. 4. Здесь
рансформатор
с ферромагнитным
сердечником
изображен на
рис. 4. Здесь ![]() и
и
![]() -
активные
сопротивления
первичной и
вторичной
обмоток с числами
витков
-
активные
сопротивления
первичной и
вторичной
обмоток с числами
витков ![]() и
и
![]() соответственно.
соответственно.
![]() -
основной поток,
замыкающийся
по сердечнику.
-
основной поток,
замыкающийся
по сердечнику.
![]() и
и
![]() -
потоки рассеяния
первичной и
вторичной
обмоток, которым
соответствуют
индуктивности
рассеяния
-
потоки рассеяния
первичной и
вторичной
обмоток, которым
соответствуют
индуктивности
рассеяния ![]() и
и
![]() и
индуктивные
сопротивления
рассеяния
и
индуктивные
сопротивления
рассеяния ![]() и
и
![]() .
.
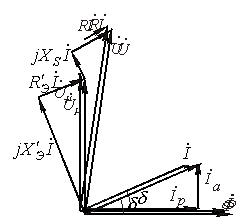
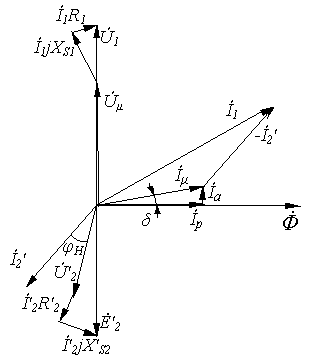
Основные соотношения, схема замещения и векторная диаграмма для трансформатора с ферромагнитным сердечником приведены в табл. 2.
Таблица 2. Трансформатор с ферромагнитным сердечником
| Вид информации | Уравнения, соотношения, векторная диаграмма | Примечание | ||||
| Уравнения для первичной и вторичной цепей Коэффициент трансформации Параметры вторичной цепи, приведенные к первичной: напряжение на нагрузке ток ЭДС сопротивление вторичной обмотки сопротивление нагрузки Уравнения приведенного трансформатора |
где где
| У правильно сконструирован-ных трансформато-ров при нагрузке, близкой к номинальной,
| ||||
| Схема замещения |
|
Выражения для | ||||
| Векторная диаграмма |
| Диаграмма строится, начиная со вторичного контура, для произвольного расположения - угол нагрузки |
Литература
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Контрольные вопросы и задачи
Из каких составляющих складываются общие потери в стали сердечника ?
Как на практике подсчитываются потери в стали и намагничивающая мощность ?
Объясните понятия комплексной магнитной проницаемости и комплексного магнитного сопротивления.
Нарисуйте последовательную и параллельную схемы замещения катушки с ферромагнитным сердечником и соответствующие им векторные диаграммы.
Как определяются параметры ![]() и
и ![]() сердечника ?
сердечника ?
Как в схеме замещения нелинейной катушки учитывается воздушный зазор в сердечнике ?
Нарисуйте схему замещения и векторную диаграмму для трансформатора с ферромагнитным сердечником.
Катушка со стальным сердечником, имеющим ![]() , сечение
, сечение ![]() , длину
, длину ![]() и воздушный зазор
и воздушный зазор ![]() , включена на переменное напряжение
, включена на переменное напряжение ![]() ; число витков обмотки
; число витков обмотки ![]() . Пренебрегая рассеянием и потерями в стали сердечника и считая активное сопротивление обмотки равным 100 Ом, определить потребляемый ток и активную мощность.
. Пренебрегая рассеянием и потерями в стали сердечника и считая активное сопротивление обмотки равным 100 Ом, определить потребляемый ток и активную мощность.
Ответ:
![]() .
.
При напряжении с действующим значением ![]() и частотой
и частотой ![]() на зажимах дросселя ток в его обмотке
на зажимах дросселя ток в его обмотке ![]() , а потребляемая мощность
, а потребляемая мощность ![]() . Число витков обмотки дросселя
. Число витков обмотки дросселя ![]() , а ее активное сопротивление
, а ее активное сопротивление ![]() . Измерения показали, что максимальное значение рабочего потока в сердечнике
. Измерения показали, что максимальное значение рабочего потока в сердечнике ![]() . Определить параметры элементов параллельной схемы замещения дросселя.
. Определить параметры элементов параллельной схемы замещения дросселя.
Ответ:
![]() .
.
Лекция N 38
Переходные процессы в нелинейных цепях![]()
Особенности расчета переходных процессов в нелинейных цепях
Переходные процессы в нелинейных электрических цепях описываются нелинейными дифференциальными уравнениями, общих методов интегрирования которых не существует. На нелинейные цепи не распространяется принцип суперпозиции, поэтому основанные на нем методы, в частности классический или с использованием интеграла Дюамеля, для расчета данных цепей не применимы.
Анализ переходных режимов в электрических цепях требует использования динамических характеристик нелинейных элементов, которые, в свою очередь, зависят от происходящих в них динамических процессов и, следовательно, в общем случае наперед неизвестны. Указанное изначально обусловливает в той или иной степени приближенный характер расчета переходных процессов.
Переходный процесс в нелинейной цепи может характеризоваться переменной скоростью его протекания в различные интервалы времени. Поэтому понятие постоянной времени в общем случае не применимо для оценки интенсивности протекания динамического режима.
Отсутствие общности подхода к интегрированию нелинейных дифференциальных уравнений обусловило наличие в математике большого числа разнообразных методов их решения, нацеленных на различные типы уравнений. Применительно к задачам электротехники все методы расчета по своей сущности могут быть разделены на три группы:
– аналитические методы, предполагающие либо аналитическое выражение характеристик нелинейных элементов, либо их кусочно-линейную аппроксимацию;
– графические методы, основными операциями в которых являются графические построения, часто сопровождаемые вспомогательными вычислительными этапами;
– численные методы, основанные на замене дифференциальных уравнений алгебраическими для приращений переменных за соответствующие интервалы времени.
Аналитические методы расчета
Аналитическими называются методы решения, базирующиеся на аналитическом интегрировании дифференциальных уравнений, описывающих состояние нелинейной цепи с использованием аналитических выражений характеристик нелинейных элементов.
Основными аналитическими методами, используемыми при решении широкого круга задач электротехники, являются:
– метод условной линеаризации;
– метод аналитической аппроксимации;
– метод кусочно-линейной аппроксимации.
Метод условной линеаризации
Метод
условной линеаризации
применяется
в случаях, когда
в нелинейном
уравнении одно
из слагаемых
в левой части
мало по сравнению
с другими, вследствие
чего, без внесения
существенной
погрешности,
его можно
соответствующим
образом линеаризовать.
Благодаря этому
все уравнение
становится
линейным для
одной из переменных,
определяющих
характеристику
![]() нелинейного
элемента, например
нелинейного
элемента, например
![]() .
С использованием
этой характеристики
находится затем
временная
зависимость
.
С использованием
этой характеристики
находится затем
временная
зависимость
![]() для
второй определяющей
ее переменной
по алгоритму:
для
второй определяющей
ее переменной
по алгоритму:
![]() .
.
Метод отличается простотой, однако получаемое с его использованием решение является достаточно приближенным, вследствие чего он в основном применяется для ориентировочных расчетов.
В
качестве примера
использования
метода определим
максимальное
значение тока
в цепи на рис.
1, если ![]() , где
, где ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Вебер–амперная характеристика нелинейной катушки индуктивности приведена на рис. 2.
.
Вебер–амперная характеристика нелинейной катушки индуктивности приведена на рис. 2.
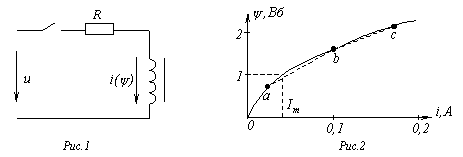
Похожие работы
... 4 Содержание отчета Схема включения однофазного счетчика в сеть. Схема включения трехфазного счетчика (п.7). Таблица с результатами измеренных и вычисленных значений. 3. Выводы о результатах поверки счетчика. Контрольные вопросы. 1. Единицы измерения электрической энергии. 2. Основные части счетчика и их назначение. 3. Принцип работы индукционного ...
... задач и выдвигать гипотезы , которые могут быть подтверждены или опровержены. Знания могут быть получены в процессе наблюдения за каким-либо объектогм. Режимы работы инженера по знаниям, консультолога в процессе приобретения знаний. протокольный анализ записываются рассуждения вслух в процессе решения задач. О.с. составляются протоколы, которые анализируются Интервью - ведется диалог с ...
... Сибири».5. Заключение В своем реферате я попытался раскрыть некоторые стороны жизней Неелова, Артамонова, Ремезова и Рябкова. Все они выходцы из ТИИ и все они добились своей цели в жизни, стали высокими людьми и никогда, наверное, не забудут свои студенческие годы. Биография каждого представленного кандидата раскрыта, показаны их жизненные пути, взлеты и падения. Каждый из них благодарен инс
... оказывает религиозное сознание японцев и дух коллективизма, зачастую посетителей какого либо парка, музея или кинотеатра являются служащими какой-либо из фирм. 2.3 Традиции организации досуга в Японии Традиционные формы проведения досуга занимают огромное место в жизни японцев. И по сей день существуют клубы любителей чая, проводятся соревнования составителей ароматов – кодо. ДО сих пор гейша ...
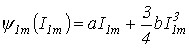 .
. 
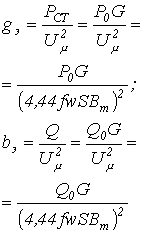
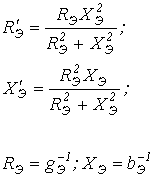
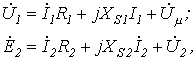
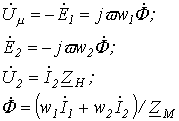
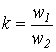
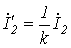
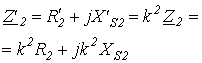
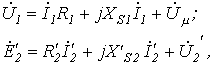
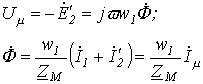
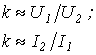
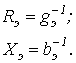
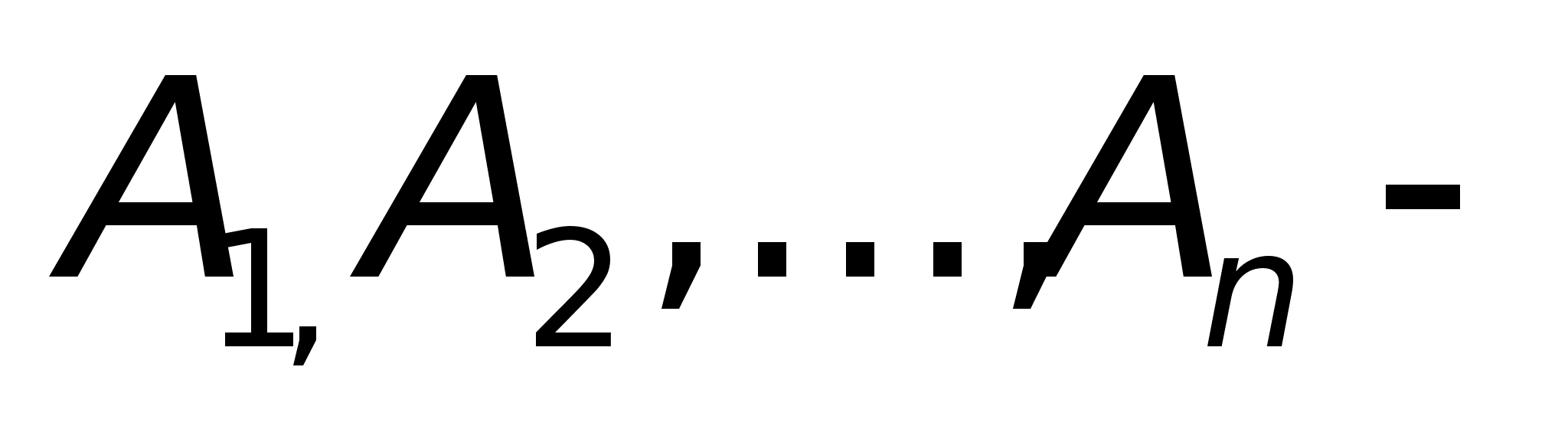
0 комментариев