Двухфазная
система Тесла
Конденсатор
Независимо
от способа
соединения
– в звезду или
в треугольник
– линейные
напряжения
не содержат
гармоник, кратных
трем
Посредством
обратного
преобразования
Лапласа
Прямая” задача
для неразветвленной
магнитной цепи
В соответствии
с первым законом
Кирхгофа
В соответствии
с заданной ВАХ
нелинейный
резистор на
участке 1-2 заменяем
линейным резистором
с сопротивлением
Запишем уравнение состояния цепи после коммутации
Подставив в уравнение переходного процесса
Решением первого уравнения является
Метод фазовой
плоскости
Нарисуем расчетную
дискретную
схему замещения
цепи (см. рис.
4)
Навигация
Запишем уравнение состояния цепи после коммутации
Лекции по ТОЭ
352659
знаков
353
таблицы
269
изображений
1. Запишем уравнение состояния цепи после коммутации
|
| (1) |
.2. Используя метод условной линеаризации, определим второе слагаемое в левой части (1) как
|
| (2) |
,где
;
и 
- амплитуды потокосцепления и тока в установившемся послекоммутационном режиме; 
.
3. Подставив (2) в (1), получим линейное дифференциальное уравнение
,
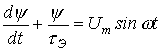решением которого на основании классического метода расчета переходных процессов является
.
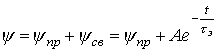4. Принужденная составляющая 
определяется соотношением
,
где 
.
Для определения и 
предположим
(с последующей проверкой), что
. При этом условии
и 
. По зависимости
для полученного значения найдем 
.Тогда 
и 
, т.е. сделанное выше предположение корректно.
Следует отметить, что в общем случае значения
и могут быть определены, например, итерационным методом.
Определив 
, запишем
.
Поскольку по условию 
, то
.
Таким образом,
|
| (3) |
. 6.
Не решая трансцендентное уравнение, будем считать, что максимальное значение потокосцепления имеет место примерно через полпериода своего изменения, т.е. при
. Подставив это время в (3), получим:
По кривой
для
найдем максимальное значение тока 
, которое в 
раз превышает амплитуду тока в установившемся послекоммутационном режиме. Напомним, что для линейной цепи 
Примечания: 1. Обычно при использовании метода условной линеаризации для расчета переходного процесса при подключении нелинейной катушки индуктивности к источнику синусоидального напряжения эквивалентная линейная индуктивность 
определяется исходя из амплитудных значений тока и потокосцепления в установившемся послекоммутационном режиме, как это и было сделано в рассмотренном выше примере. Однако если необходимо оценить максимально возможное значение тока, то величину индуктивности следует определять по начальному участку вебер–амперной характеристики, где
максимальна.
2.
Если сопротивление резистора в ветви с нелинейной катушкой достаточно велико, так
что
, то следует пренебречь нелинейностью слагаемого 
, положив
. В этом случае нелинейное уравнение (1) сводится к линейному вида
,
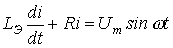и соответственно кривая
определяется по кривым 
и
.
Метод аналитической аппроксимации
Метод основан на аппроксимации характеристики нелинейного элемента аналитической функцией, которая должна, с одной стороны, достаточно точно отображать исходную нелинейную характеристику на участке перемещения рабочей точки, а с другой стороны, обеспечивать возможность достаточно несложного интегрирования полученного дифференциального уравнения (в частности, с использованием табличных интегралов).
Метод применим к нелинейным цепям с одним накопителем энергии, описываемым дифференциальными уравнениями первого порядка, а также к цепям, описываемым уравнениями, сводящимися к уравнениям первого порядка путем замены переменных.
Ц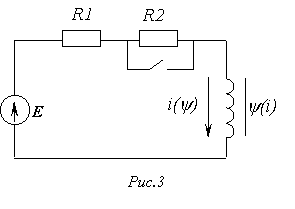
енность метода заключается в получении выражения исследуемой величины в
общем виде, что
позволяет осуществлять требуемый анализ процессов при варьировании параметров схемы.
В
качестве примера
использования
метода определим
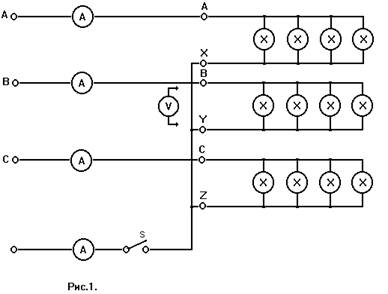
ток в схеме на
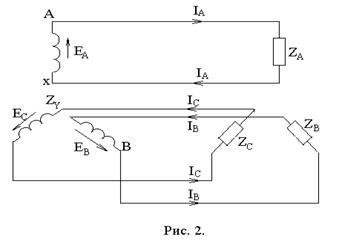
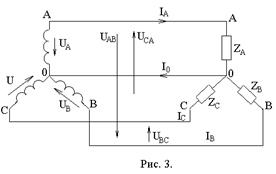
рис. 3, полагая,
что характеристика
нелинейной
катушки имеет
вид типовой
кривой на рис.
2.
1.
Для решения задачи выберем выражение аналитической аппроксимации вида 
. Определяя параметр
из условия соответствия данной функции точке установившегося послекоммутационного режима, получим
|
| (4) |
, где 
.
Похожие работы
... 4 Содержание отчета Схема включения однофазного счетчика в сеть. Схема включения трехфазного счетчика (п.7). Таблица с результатами измеренных и вычисленных значений. 3. Выводы о результатах поверки счетчика. Контрольные вопросы. 1. Единицы измерения электрической энергии. 2. Основные части счетчика и их назначение. 3. Принцип работы индукционного ...
... задач и выдвигать гипотезы , которые могут быть подтверждены или опровержены. Знания могут быть получены в процессе наблюдения за каким-либо объектогм. Режимы работы инженера по знаниям, консультолога в процессе приобретения знаний. протокольный анализ записываются рассуждения вслух в процессе решения задач. О.с. составляются протоколы, которые анализируются Интервью - ведется диалог с ...
... Сибири».5. Заключение В своем реферате я попытался раскрыть некоторые стороны жизней Неелова, Артамонова, Ремезова и Рябкова. Все они выходцы из ТИИ и все они добились своей цели в жизни, стали высокими людьми и никогда, наверное, не забудут свои студенческие годы. Биография каждого представленного кандидата раскрыта, показаны их жизненные пути, взлеты и падения. Каждый из них благодарен инс
... оказывает религиозное сознание японцев и дух коллективизма, зачастую посетителей какого либо парка, музея или кинотеатра являются служащими какой-либо из фирм. 2.3 Традиции организации досуга в Японии Традиционные формы проведения досуга занимают огромное место в жизни японцев. И по сей день существуют клубы любителей чая, проводятся соревнования составителей ароматов – кодо. ДО сих пор гейша ...
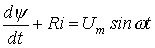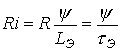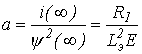0 комментариев