Навигация
ЭФФЕКТИВНОСТЬ ПОРТФЕЛЯ. ДИВЕРСИФИКАЦИЯ
2.2. ЭФФЕКТИВНОСТЬ ПОРТФЕЛЯ. ДИВЕРСИФИКАЦИЯ.
Предположим, что инвестор купил какую-либо ценную бумагу по известной цене и через некоторое время намеревается продать ее по заранее не известной цене, а также за время владения этой бумагой инвестор рассчитывает получить дивиденды в неизвестном объеме.
Эффективность такой операции можно считать случайной величиной X. За период времени t эффективность ценной бумаги
Xt = Ct+1 - Ct / Ct
Где Ct+1 - цена продажи бумаги в (t+1)-й момент времени;
Ct - цена покупки бумаги в t-й момент времени.
Ожидаемой эффективностью (эффектом) будем считать математическое ожидание случайной величины X:
m = E(X)
Доход, получаемый инвестором от вложений в ценные бумаги, неизменно сопряжен с риском, представляющим собой возможность возникновения обстоятельств, при которых инвестор может понести потери. Принято выделять два типа рисков: систематический и несистематический.
Систематический риск определяется глобальными обстоятельствами, не зависящими от инвестора и эмитента. К таким обстоятельствам можно отнести политические события на уровне страны и на международном уровне, изменения законодательства, экономические реформы и т.д.
Несистематический риск определяется факторами, связанными с деятельностью предприятия-эмитента и изменениями рыночной конъюнктуры. Несистематический риск можно уменьшить путем диверсификации портфеля; систематический же риск путем диверсификации уменьшить нельзя.
Можно составить безрисковый портфель, но отсутствие риска для него будет означать отсутствие только несистематического риска, систематический риск остается. Например, а российских условиях безрисковым портфелем является портфель в иностранной валюте (долларах CША), но и он подвержен систематическому риску, связанному, например, с возможными изменениями законодательства, касающимися ограничений обращения иностранной валюты на территории России.
Если в течение длительного времени держать средства в виде безрисковых активов, то и доход от них будет нулевым, поэтому большинство инвесторов опасается риска, но идет на некоторый риск, если он компенсируется дополнительным доходом.
В качестве меры риска, считая эффективность некоторой ценной бумаги случайной величиной X, можно принять ее вариацию (дисперсию)
V=E{(X-m)2},
поскольку V представляет собой квадрат отклонения X от ожидаемого значения т. Если нет отклонения, т.е. V = О, то и риска нет, чем больше V, тем больше риск. Возникает вопрос, какой риск описывается величиной V. Это зависит от того, какому риску подвергаются инвесторы в период времени, по которому выбирается статистика.
Для моделирования портфеля важное значение будет иметь величина стандартного (среднеквадратичного) отклонения и ковариация двух случайных величин X1 , X2:
V12 = Е{( X1 –т1 )( X2–т2 )}.
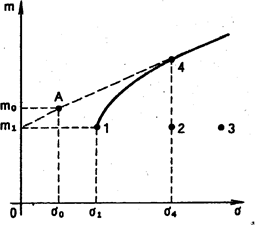
Рис. 1. Эффективные портфели
Предположим теперь, что имеется четыре различных портфеля, отмеченных на рис. 1 точками 7, 2,3,4 с координатами mi (i = 1, 2, 3, 4). Портфели, лежащие правее, имеют больший риск. Портфели, которым соответствуют точки, находящиеся выше, имеют больший эффект. Очевидно, что опытный инвестор будет действовать при выборе из двух портфелей Xi и Xj следующим образом: он выберет Xi если выполняются одно из условий:
E(Xi)=E(Xj), s (Xi) < s (Xj);
E(Xj)>E(Xj), s (Xi)= s (Xj ).
На графике этот выбор означает из первого и второго портфелей первый (точка 1), из четвертого и второго - четвертый портфель (точка 4) В других случаях, когда
E(Xi)=E(Xj), s (Xi) < s (Xj)
каждый инвестор поступит соответственно своим предпочтениям и своей склонности к риску. Однако если из всех возможных вариантов портфелей выбрать все портфели, которые при каждом заданном уровне риска имеют максимальную ожидаемую эффективность (доходность) а при заданном уровне доходности имеют минимальный риск то это подмножество портфелей будет описываться кривой 1.- 4 (см рис 1)
Такие портфели называются эффективными, а кривая 7 - 4 представляет множество эффективных портфелей. Остальные возможные портфели представляют собой множество неэффективных портфелей Из двух портфелей лучше тот, который находится ближе к множеству эффективных портфелей. Среди эффективных портфелей инвестор должен выбрать один, наиболее для него предпочтительный (оптимальный) На рис. 1 эффективными являются портфели 7 и 4, неэффективными - 2 и 3
Добавим теперь портфель с нулевым риском и гарантированной ожидаемой эффективностью m . Для нового множества допустимых портфелей граница эффективности теперь изменится и будет описываться кривой m - 4. Для этого множества портфелей портфель 1 перестал быть эффективным, так как портфель т имеет меньший риск чем портфель 1 при одинаковой норме доходности.
Если инвестор согласен на риск в своем портфеле, то оптимальным для него будет портфель А со значениями риска о и ожидаемой эффективности m Такой портфель можно сформировать, если взять долю s0 / s4 безрисковых вложений и долю (s4-s0)/ s4 вложений из портфеля 4.
Практика показывает, что с увеличением количества видов ценных бумаг в портфеле уменьшается риск инвестиций. Это происходит потому, что в портфель включаются ценные бумаги, слабокоррелированные между собой, только в этом случае возможно снижение риска Процедура включения в портфель различных видов ценных бумаг, имеющих низкий коэффициент корреляции, называется диверсификацией
При диверсификации риск портфеля снижается только до определенного уровня, ниже которого путем диверсификации риск уменьшить нельзя. Таким образом, риск представляет собой сумму диверсифицируемого и недиверсифицируемого рисков. Диверсифицируемая часть риска представляет собой несистематический риск, а недиверсифицируемая - систематический.
Если задать желаемый для инвестора уровень доходности портфеля, то можно поставить задачу выбора такой структуры портфеля, которая при заданном уровне доходности приводила бы к минимальному риску. Математическая постановка такой задачи впервые была сформулирована в 1951 г. Г. Марковицем.
Для решения задачи Г. Марковица статистическими методами требуется большой объем данных о рынке ценных бумаг, накопленных за многие годы и отвечающих условиям представительности. На практике, особенно на российском фондовом рынке, который еще только формируется, такие данные получить очень трудно, а подчас и невозможно. В настоящее время появились различные эвристические методы для решения подобных задач, дающие псевдооптимальные решения, например различные генетические алгоритмы. Тем не менее традиционно для принятия решений о формировании портфеля пользуются моделью оценки финансовых активов (Capital Asset Pricing Model - САРМ), представляющей собой зависимость между эффективностью (доходностью) конкретной ценной бумаги и эффективностью рыночного портфеля (портфеля, содержащего все бумаги, находящиеся на рынке).
В САРМ-модели предполагается, что эффективность ценной бумаги Х линейно зависит от некоторого ведущего фактора F, описывающего эффективность рынка в целом, и в то же время на каждую j ценную бумагу влияют и специфические для нее факторы, являющиеся случайными величинами е. Тогда
Xj = aj +bj F + ej ,
где aj и bj - некоторые детерминированные величины, а коэффициент bj отражает зависимость эффективности бумаги от рыночной конъюнктуры, если bj > О, то эффект бумаги аналогичен эффекту рынка, если bj < 0, то эффективность бумаги возрастает, когда эффективность рынка снижается.
Эта модель эффективности ценной бумаги носит название индексной модели У. Шарпа.
Для характеристики конкретной ценной бумаги используются и другие параметры. Если отсчитывать эффективность инвестиций в ценную бумагу от эффективности безрискового вклада r , то параметр
aj = aj - bj r0
представляет собой превышение эффективности ценной бумаги над безрисковой эффективностью (можно считать это некоторой премией за риск). Если aj < 0, то рыночная цена на эту бумагу завышена, и в ближайшем будущем она может понизиться; если же aj > 0, то рыночная цена занижена, и в будущем вероятно ее повышение. Следовательно, при прочих равных условиях более предпочтительна бумага с aj > 0.
На западных рынках значения а, b и R2 регулярно рассчитываются для всех ценных бумаг и публикуются вместе с индексами. Пользуясь этой информацией, инвестор может сформировать собственный портфель ценных бумаг. На российском рынке профессионалы постепенно тоже начинают использовать а-, b- R2 - анализ. Отдельные инвестиционные институты рассчитывают а, b и R2 .
Похожие работы
... ), должна выкупить свои бумаги по номиналу. По соглашению с держателями (владельцами) облигаций выкуп может производиться путем обмена облигаций на собственные акции организации, ценные бумаги других эмитентов, любые другие активы.3 АУДИТ ОПЕРАЦИЙ С ЦЕННЫМИ БУМАГАМИ 3.1 Цель и задачи аудита операций с ценными бумагами Аудиторская проверка операций с ценными бумагами проводится в целях ...
... полностью или частично направляются на реинвестирование, то на эту сумму делается проводка по дебету счета 06 “Долгосрочные финансовые вложения” и кредиту счета 80. Письмом МФ РФ от 23.12.92 г. №117 “Об отражении в бухгалтерском учете и отчетности операций, связанных с приватизацией предприятия” разработан порядок отражения в бухгалтерском учете операций с акциями. При приобретении акций ...
... 3. Обзор существующих систем автоматизации back-office; 3. Ориентировочная тема дипломного проекта Учет операций с ценными бумагами. Руководитель Блат И. Д. Содержание 1 Введение 6 2 Предприятие 7 2.1 Характеристика компании и виды оказываемых ...
... особенностей налогообложения таких операций РЕПО. Глава 2. ЦЕННЫЕ БУМАГИ, ДЕНОМИНИРОВАННЫЕ В ВАЛЮТЕ Операции с ценными бумагами являются одними из наиболее сложных вопросов ввиду их специфического порядка обращения. В главе 25 НК РФ установлены особенности определения налоговой базы при налогообложении доходов от реализации ценных бумаг в зависимости от категории. В налоговом учете расходы ...
0 комментариев