Навигация
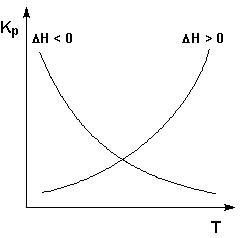
Электропроводность электролитов
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Белгородская государственная технологическая академия строительных материалов
Кафедра физической и коллоидной химии
КУРСОВАЯ РАБОТА
НА ТЕМУ:
«Электропроводность электролитов»
Выполнил: ст. гр. ПЭ-31
Спирин М.Н.
Проверил: Лопанов А.Н.
БЕЛГОРОД 2001
Содержание:
Введение……………………………………………………………….3
1. Электропроводность электролитов…………………………………..4
1.1. Удельная и молярная электропроводности…….…….…..……..4
1.2. Эквивалентная электропроводность…………………………….7
2. Подвижность ионов……………………………………………...……9
2.1. Зависимость подвижности ионов от температуры…………....11
2.2. Зависимость подвижности ионов от
кристаллохимических радиусов………………………………..12
3. Аномальная подвижность ионов гидроксония
и гидроксила………………………………………………………….14
4. Числа переноса……………………………………………………….16
5. Закон разбавления Оствальда………………………………………..19
6. Электрофоретический и релаксационный эффекты
в электролитах, их влияние на электрическую проводимость……22
7. Методы измерения электропроводности электролитов………..….25
Заключение…………………………………………………………..27
Список используемой литературы…………………………………28
Введение
Электролиты (от электро и греч. lytos - разлагаемый, растворимый), жидкие или твёрдые вещества и системы, в которых присутствуют в сколько-нибудь заметной концентрации ионы, обусловливающие прохождение электрического тока. В узком смысле электролиты называются вещества, растворы которых проводят электрический ток ионами, образующимися в результате электролитической диссоциации. Электролиты в растворах подразделяют на сильные и слабые. Сильные электролиты практически полностью диссоциированы на ионы в разбавленных растворах. К ним относятся многие неорганические соли и некоторые неорганические кислоты и основания в водных растворах, а также в растворителях, обладающих высокой диссоциирующей способностью (спирты, амиды и др.). Молекулы слабых электролитов в растворах лишь частично диссоциированы на ионы, которые находятся в динамическом равновесии с недиссоциированными молекулами. К слабым электролитам относится большинство органических кислот и многие органические основания в водных и неводных растворах. Деление электролитов на сильные и слабые в некоторой степени условно, т. к. оно отражает не свойства самих электролитов, а их состояние в растворе. Последнее зависит от концентрации, природы растворителя, температуры, давления и др.
По количеству ионов, на которые диссоциирует в растворе одна молекула, различают бинарные, или одно-одновалентные электролиты (обозначаются 1-1 электролит, например КС1), одно-двухвалентные электролиты (обозначаются 1-2 электролит, например CaCl2) и т. д. Электролиты типа 1-1, 2-2, 3-3 и т. п. называются симметричными, типа 1-2, 1-3 и т. п. - несимметричными.
Свойства разбавленных растворов слабых электролитов удовлетворительно описываются классической теорией электролитической диссоциации. Для не слишком разбавленных растворов слабых электролитов, а также для растворов сильных электролитов эта теория неприменима, поскольку они являются сложными системами, состоящими из ионов, недиссоциированных молекул или ионных пар, а также более крупных агрегатов. Свойства таких растворов определяются характером взаимодействий ион-ион, ион-растворитель, а также изменением свойств и структуры растворителя под влиянием растворённых частиц. Современные статистические теории сильных электролитов удовлетворительно описывают свойства лишь очень разбавленных (<0,1 моль/л) растворов.
1. Электропроводность электролитов.
1.1.Удельная и молярная электропроводности электролитов.
Электрическая проводимость растворов электролитов, т.е. способность их проводить электрический ток, зависит от природы электролита и растворителя, концентрации, температуры и некоторых других факторов. Различают удельную и молярную электрическую проводимости.
Удельная электрическая проводимость раствора электролита x – это электрическая проводимость объема раствора, заключенного между двумя параллельными электродами, имеющими площадь по одному квадратному метру и расположенными на расстоянии одного метра друг от друга.
Удельная электрическая проводимость является величиной, обратной удельному сопротивлению ρ:
(1)
Удельное сопротивление определяется по уравнению
(2)
где R — общее сопротивление проводника. Ом; l — длина проводника, м; s — поперечное сечение проводника, м2. Из уравнения (2) имеем:
ρ=Rs/l. (3)
Полученное выражение показывает, что размерность, т. е. единица удельного сопротивления, выражается величиной [ρ]=0м м.
Единица удельной электрической проводимости, т. е. размерность ее, выражается обратной величиной x=1/(0м м) = Oм-l•м-l = Cм м-1.
Повышение температуры на 1 К увеличивает удельную электрическую проводимость примерно на 2 - 2,5%. Это объясняется понижением вязкости раствора и уменьшением гидратации ионов, а для растворов слабых электролитов увеличением их степени диссоциации.
Зависимость удельной электрической проводимости разбавленных растворов от температуры описывается эмпирическим уравнением
xT = x298 [1 + α (T - 298) +β (Т- 298)2];
(4)
β = 0,0163 (α - 0,0174),
где x298 – удельная электрическая проводимость при 298 К; α и β - температурные коэффициенты электрической проводимости. Коэффициенты α и β зависят от природы электролита: для сильных кислот α = 0,0164, для сильных оснований α = 0,0190, для солей α = 0,0220.
В растворах слабых электролитов диссоциация молекул электролита на ионы увеличивает объем раствора. Поэтому повышение давления в соответствии с принципом смещения подвижного равновесия Ле Шателье – Брауна уменьшает степень диссоциации электролита и, следовательно, электрическую проводимость. Заметное влияние на электрическую проводимость раствора слабого электролита оказывает только давление порядка сотен и тысяч атмосфер. Например, повышение давления до 2000 атм уменьшает x для уксусной кислоты на 40%.
При изучении электрической проводимости растворов целесообразно пользоваться молярной электрической проводимостью Λ, которая равна электрической проводимости объема раствора электролита, содержащего 1 г/моль растворенного вещества и находящегося между двумя параллельными электродами, расположенными на расстоянии одного метра друг от друга. Для слабых электролитов изменение молярной электрической проводимости от концентрации раствора связано в основном со степенью диссоциации и для сильных электролитов - с межионным взаимодействием.
Удельная и молярная электрические проводимости связаны между собой соотношением:
Λ = xVм = x/cм (5)
где Vм — число кубометров раствора, содержащего 1 г/моль электролита; См — концентрация электролита, выраженная в моль/м3. Для практических расчетов можно использовать также размерности в производных единицах СИ: [χ]=См см-1; [Λ] = См см2 •моль-1; [с] = моль/л (моль/дм3). При этом вместо уравнения (5) получаем:
(6)
При вычислении молярной электрической проводимости нужно указывать формульную единицу, для которой она вычислена. Так, например, при 298 К в водном растворе при предельном разбавлении A(MgCl2)=258 · 104 См м2 • моль-1, но Λ (MgCl2) = 129 • 104 См • м2 моль-1.
Молярная электрическая проводимость с уменьшением концентрации раствора увеличивается и при с → 0 стремится к некоторому предельному максимальному значению Λ∞, которое называется молярной электрической проводимостью при предельном (бесконечном) разбавлении. Например, для предельно разбавленных растворов НС1, КС1 и NH4OH значения Λ∞, при 298 К соответственно равны 426 · 104; 149,8 104 и 271,4 104 См м2 моль-1.
Зависимость молярной электрической проводимости от температуры можно представить уравнением:
ΛТ = Λ298 [1+α (T-298)], (7)
где ΛТ и Λ298 — молярные электрические проводимости при температуре Т = 298 К; α — температурный коэффициент электрической проводимости. Уравнение (7) справедливо для узкого интервала температур. Логарифмируя уравнение (6), получаем:
(8)
Беря производную по температуре от уравнения (8), находим:
, или (9)
Из уравнения (9) следует, что температурные коэффициенты удельной и молярной электрической проводимости одинаковы.
Рассмотрим зависимость молярной электрической проводимости раствора бинарного электролита от скорости движения ионов. Пусть электрический ток проходит через раствор бинарного электролита, помещенный в стеклянную трубку с поперечным сечением s м2, причем расстояние между электродами равно l м и разность потенциалов между ними равна Е В. Обозначим через u'+ и u'- скорости движения катионов и анионов, м/с, а через см концентрацию раствора электролита, г/моль/м3. Если степень диссоциации электролита в данном растворе равна α, то концентрации катионов и анионов равны αсм г/моль/м3. Подсчитаем количество электричества, которое переносится через поперечное сечение трубки за 1 с. Катионов за это время пройдет через сечение u'+sαcм г/моль и они перенесут u'+sαcмF Кл электричества, так как г/моль переносит количество электричества, равное числу Фарадея F. Анионы в обратном направлении перенесут u'-sαcмF Кл электричества. Сила тока I, т. е. общее количество электричества, проходящее через данное поперечное сечение раствора в 1 с, равна сумме количеств электричества, переносимого ионами в обоих направлениях:
I = (u'+ + u'-)sαcмF u'+ = u+ (10)
Скорость движения ионов u'+ и u'- прямо пропорциональна напряженности поля E/l:
u'+ = u+ и u'- = u- (11)
где u+ и u- — абсолютные скорости ионов.
Абсолютной скоростью движения иона называется его скорость при единичном градиенте потенциала в 1 В м-1; ее размерность [ui] = В м2 с-1
Подставляя значения u'+ = u' - из уравнения (11) в (10), получаем
I = αF(u+ + u-) . (12)
С другой стороны, сопротивление R можно выразить через Λ. Учитывая, что из (11) ρ = 1/х и из (5) х = см Λ, получаем из (2) выражение R=l/(хs) = l/(cмΛs). Из закона Ома
I = = Λ . (13)
Приравнивая правые части уравнений (12) и (13) и решая равенство относительно Λ, получаем
Λ= αF(u+ + u-) (14)
Для сильных электролитов α=1 и
Λ= F(u+ + u-) (15)
Произведения
Fu+=λ+ и Fu-=λ- (16)
Называются подвижностями ионов; их размерность [λи] = См м моль -1. Например, в водном растворе при 298 К подвижности катионов К +, Ag+ и Mg2+ равны 73,5 · 104; 61,9 · 104 и 53,0 · 104 См м2 · моль-1 и подвижности анионов С1-1, SO42- и СН3СОО- - 76,3 104; 80,0 · 104 и 40,9 · 104 См м2 моль-1 соответственно.
Вводя значения λ+ и λ- в (14) и (15), получаем для слабых электролитов:
Λ= α(λ+ + λ-) (17)
и для сильных электролитов
Λ= λ+ + λ- (18)
Для предельно разбавленного раствора α = 1, поэтому
Λ∞ = λ + λ (19)
где λ и λ - подвижности ионов при предельном разведении. Уравнение (19), справедливое как для сильных, так и для слабых электролитов, называется законом Кольрауша, согласно которому молярная электрическая проводимость при предельном разведении равна сумме подвижностей ионов при предельном разведении. Из уравнения (19) и (16) получаем:
Λ∞ = F(u + u) (20)
где F – постоянная Фарадея; u и u - абсолютные скорости движения ионов при предельном разведении.
1.2. Эквивалентная электропроводностьЭквивалентная электропроводность λ [в см2/(г-экв Ом) вычисляется из соотношения:
(21)
где с — эквивалентная концентрация, г-экв/л.
 Эквивалентная электропроводность — это электропроводность такого объема (φ см3) раствора, в котором содержится 1 г-экв растворенного вещества, причем электроды находятся на расстоянии 1 см друг от друга. Учитывая сказанное выше относительно удельной электропроводности, можно представить себе погруженные в раствор параллельные электроды на расстоянии 1 см., имеющие весьма большую площадь. Мы вырезаем мысленно на поверхности каждого электрода вдали от его краев площадь, равную φ-см2. Электропроводность раствора, заключенного между выделенными поверхностями таких электродов, имеющими площадь, равную φ- см2, и есть эквивалентная электропроводность раствора. Объем раствора между этими площадями электродов равен, очевидно, φ-см3 и содержит один грамм-эквивалент соли. Величина φ, равная 1000/с см3/г-экв, называется разведением. Между электродами, построенными указанным выше способом, при любой концентрации электролита находится 1 г-экв растворенного вещества и изменение эквивалентной электропроводности, которое обусловлено изменением концентрации, связано с изменением числа ионов, образуемых грамм-эквивалентом, т. е. с изменением степени диссоциации, и с изменением скорости движения ионов, вызываемым ионной атмосферой.
Эквивалентная электропроводность — это электропроводность такого объема (φ см3) раствора, в котором содержится 1 г-экв растворенного вещества, причем электроды находятся на расстоянии 1 см друг от друга. Учитывая сказанное выше относительно удельной электропроводности, можно представить себе погруженные в раствор параллельные электроды на расстоянии 1 см., имеющие весьма большую площадь. Мы вырезаем мысленно на поверхности каждого электрода вдали от его краев площадь, равную φ-см2. Электропроводность раствора, заключенного между выделенными поверхностями таких электродов, имеющими площадь, равную φ- см2, и есть эквивалентная электропроводность раствора. Объем раствора между этими площадями электродов равен, очевидно, φ-см3 и содержит один грамм-эквивалент соли. Величина φ, равная 1000/с см3/г-экв, называется разведением. Между электродами, построенными указанным выше способом, при любой концентрации электролита находится 1 г-экв растворенного вещества и изменение эквивалентной электропроводности, которое обусловлено изменением концентрации, связано с изменением числа ионов, образуемых грамм-эквивалентом, т. е. с изменением степени диссоциации, и с изменением скорости движения ионов, вызываемым ионной атмосферой.
Мольная электропроводность электролита — это произведение эквивалентной электропроводности на число грамм-эквивалентов в 1 моль диссоциирующего вещества.
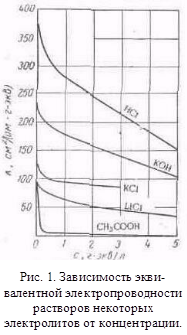
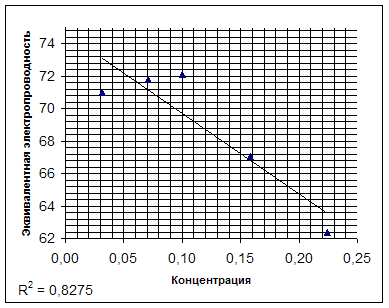
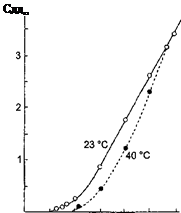
На рис. 1 показана зависимость эквивалентной электропроводности некоторых электролитов от концентрации. Из рисунка видно, что с увеличением с величина λ уменьшается сначала резко, а затем более плавно.
Интересен график зависимости λ от (2). Как видно 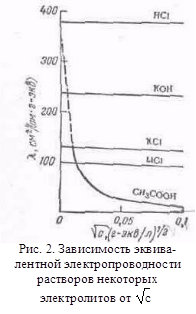 из графика (Рис. 2), для сильных электролитов соблюдается медленное линейное уменьшение λ с увеличением , что соответствует эмпирической формуле Кольрауша (1900);
из графика (Рис. 2), для сильных электролитов соблюдается медленное линейное уменьшение λ с увеличением , что соответствует эмпирической формуле Кольрауша (1900);
λ= λ∞ - А (22)
где λ∞ - предельная эквивалентная электропроводность при бесконечном разведении: с → 0; φ → ∞
Значение λ сильных электролитов растет с увеличением φ и ассимптотически приближается к λ∞. Для слабых электролитов (СН3СООН) значение λ также растет с увеличением φ, но приближение к пределу и величину предела в большинстве случаев практически нельзя установить. Все сказанное выше касалось электропроводности водных растворов. Для электролитов с другими растворителями рассмотренные закономерности сохраняются, но имеются и отступления от них, например на кривых λ-с часто наблюдается минимум (аномальная электропроводность).
Похожие работы
... к проводникам второго рода, для которых характерна ионная проводимость. Цель данной работы заключается в определении эквивалентной электропроводности лизина и установлении зависимости эквивалентной электропроводности от концентрации. Обзор литературы Мерой способности веществ проводить электрический ток является ...
... или кислот; так получают, например, золь гидроксида железа(III), имеющий следующее строение: {[Fe(OH)3]m n FeO+ · (n–x)Cl–}x+ x Cl– 4.2.2 Агрегативная устойчивость лиофобных коллоидов. Строение коллоидной мицеллы Лиофобные коллоиды обладают очень высокой поверхностной энергией и являются поэтому термодинамически неустойчивыми; это делает возможным самопроизвольный процесс уменьшения ...
... Планка; NA – число Авогадро; - приведенная масса молекулы электролита, г; сi – молярная концентрация ионов (сi= c0); с0 – исходная молярная концентрация электролита. 3. Изоморфизм уравнений При рассмотрении движения в поле вязких сил удобно ввести понятие подвижности b. Подвижность определяется как предельная скорость, приобретаемая телом под действием силы, равной единице, т. ...
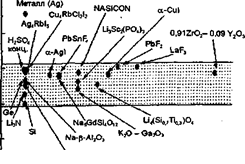
... при изучении синтеза новых материалов и процессов ионного транспорта в них. В чистом виде такие закономерности наиболее четко прослеживаются при исследовании монокристаллических твердых электролитов. В то же время при использовании твердых электролитов в качестве рабочих сред функциональных элементов необходимо учитывать, что нужны материалы заданного вида и формы, например в виде плотной керамики ...

0 комментариев