Навигация
ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ИДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА
2. ИЗМЕРЕНИЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ИДИСПЕРСИИ СЛУЧАЙНОГО ПРОЦЕССА
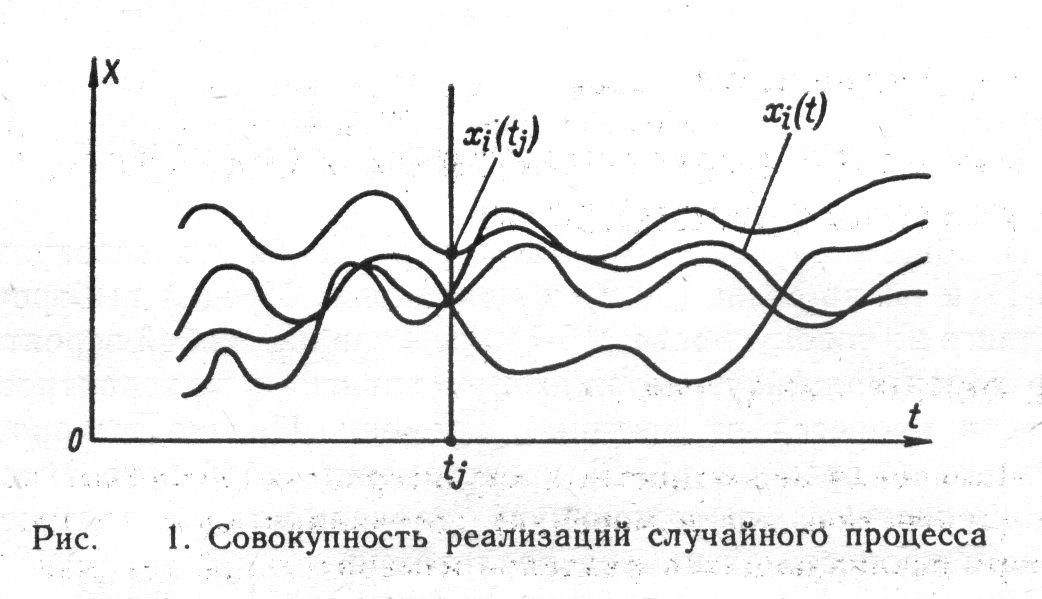
Математическое ожидание и дисперсия случайного процесса — основные числовые вероятностные характеристики, измерение которых играет большую роль в практике научных исследований, управления технологическими процессами и испытаний.
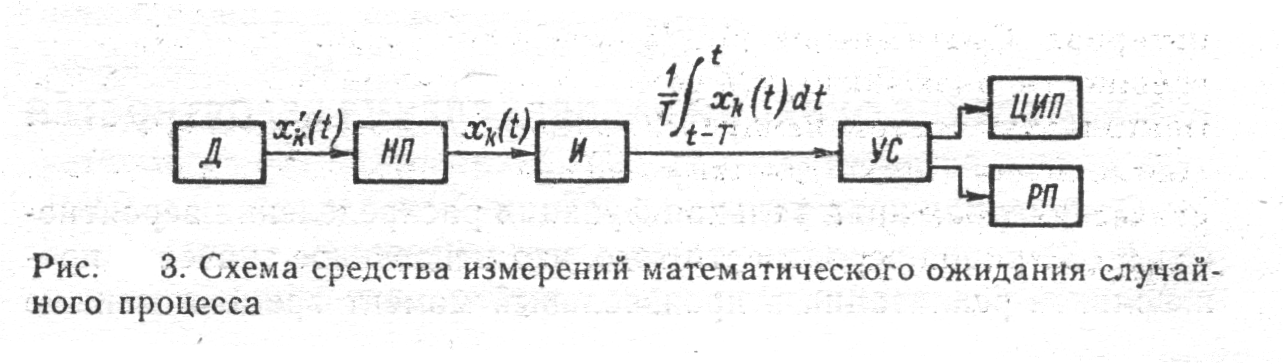
При измерении математического ожидания результатом измерения является среднее по времени или по совокупности мгновенных значений реализации исследуемого случайного процесса. Усреднение по времени применяется на практике существенно чаще, чем усреднение по совокупности, поскольку работать с одной реализацией удобнее и проще, чем с совокупностью. На рис. 3 приведена структурная схема устройства, реализующего алгоритм
t
M* [X (t)]= 1/T xk (t) dt.
t-T
На рисунке Д—преобразователь измеряемой величины в электрический сигнал (датчик); НП — нормирующий преобразователь, превращающий входной сигнал в стандартный по виду и диапазону значений; И — интегратор; УС — устройство сопряжения, обеспечивающее согласование выхода интегратора со входами цифрового вольтметра и регистрирующего прибора;
ЦИП — цифровой прибор (например, цифровой вольтметр);
РП—регистрирующий прибор (самопишущий прибор).
Для оценки среднего квадратичeского значения погрешности, обусловленной конечностью объема выборочных данных,
можно пользоваться следующими соотношениями:
1/2
=[2D[X(t)] k/T]
M
при усреднении по времени T и
1/2
=[D[X(t)]/N]
M
при усреднении по совокупности N. Здесь D[X (t)]—дисперсия процесса X(t), а k — интервал корреляции. Дисперсия случайного процесса характеризует математическое ожидание квадрата отклонений мгновенных значений реализации случайного процесса от математического ожидания. Таким образом,
T 2
D[X(t)]= lim 1/T [xk (t)-[X(t)]] dt
T 0
или
N 2
D[X(t)]= lim 1/N [xi(t)-[X(t)]] dt
N i=1
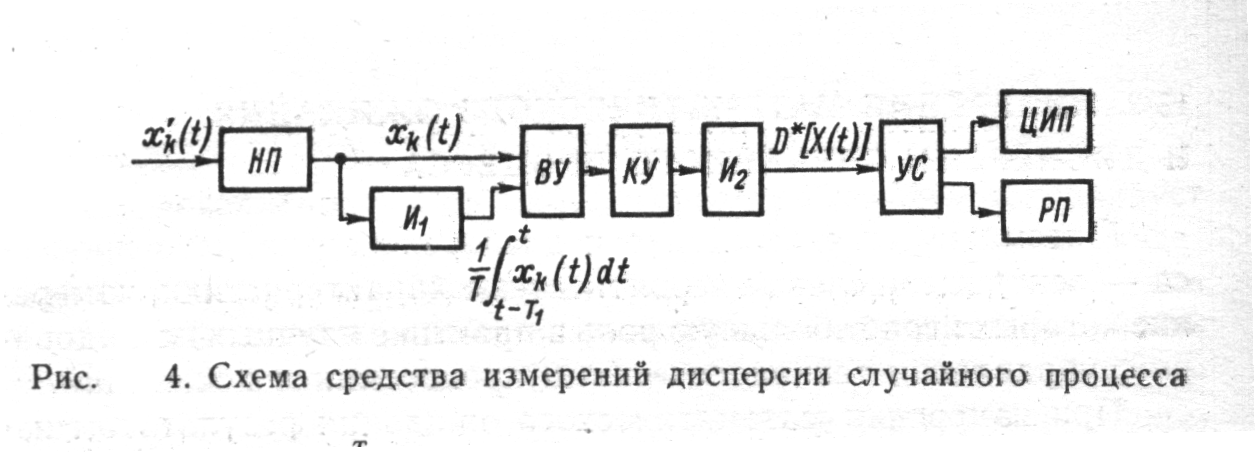
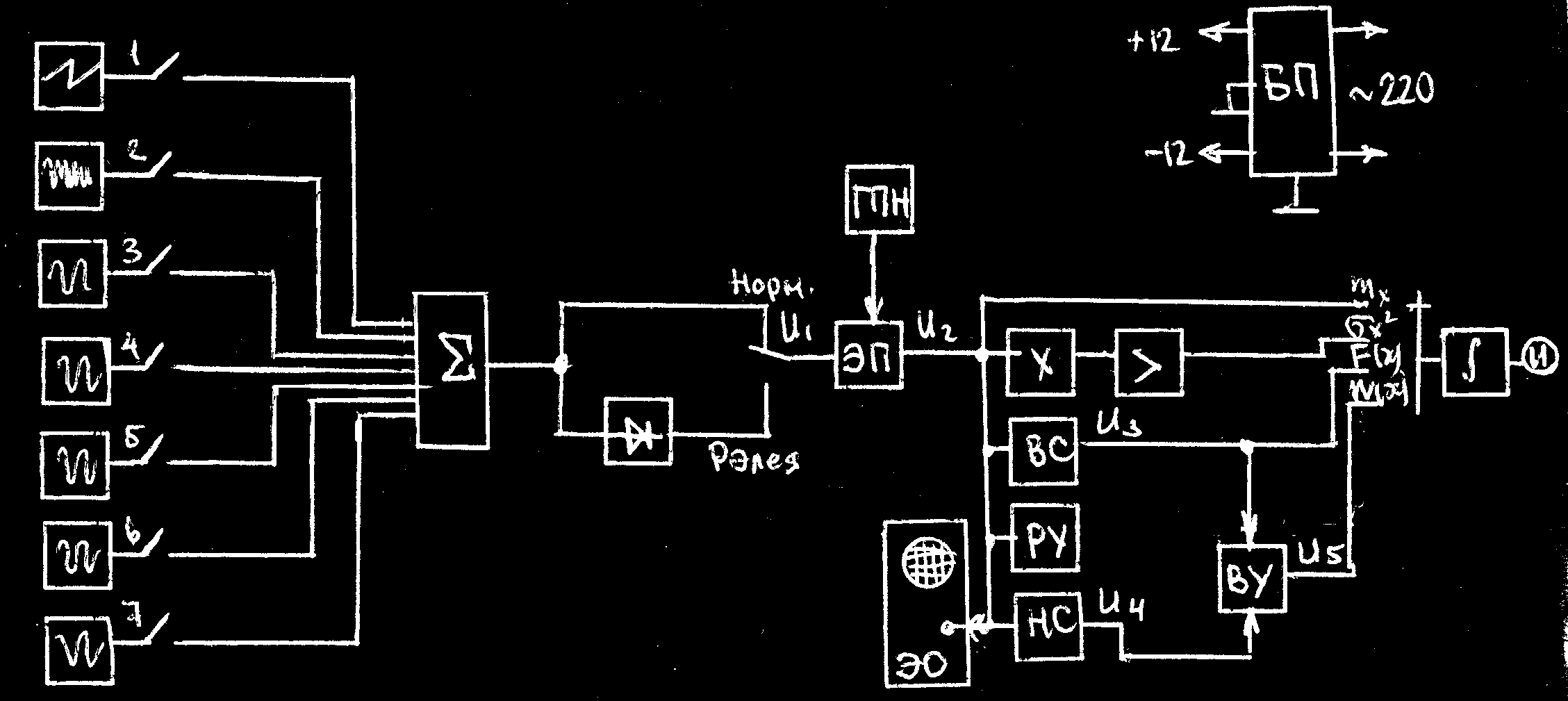
Возможны различные варианты построения устройств для измерения дисперсии случайного процесса — дисперсиометров. На рис. 4 приведена структурная схема средства измерений дисперсии случайного процесса, т. е. работающего согласно выражению
t t 2
D* [X(t)]=1/T [xk (t)- 1/T1 xk (t)dt] dt
t-T t-T1
На рисунке НП — нормирующий преобразователь; И1 и И2 — интеграторы; ВУ— вычитающее устройство; КУ— квадратирующее устройство; УС — устройство сопряжения; ЦИП — цифровой прибор; РП — регистрирующий прибор.
Средняя квадратическая погрешность из-за конечности объема выборочных данных о мгновенных значениях Х (t) может быть определена с помощью соотношений
2 1/2
=[2D[X (t)] k/T]
M
, где D[X2 (t)]— дисперсия Х (t); T—время усреднения.
При усреднении по совокупности N реализаций
2 1/2
=[D[X (t)] /N]
D
3. ИЗМЕРЕНИЕ ФУНКЦИЙ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
Одномерная интегральная функция распределения вероятности F (X) равна вероятности того, что мгновенное значение произвольной реализации в произвольный момент времени меньше установленного уровня, т. е. Xi (ti) X. Функция F (X) определяется как предел выборочного среднего:
F (X)= lim Sd [ [x (t) ,X]],
d
1 при x (t) X
Где [x(t) ,X]=
0 при x (t) > X
Поскольку интегральные F (X) и дифференциальные w (X) функции распределения вероятности связаны между собой соотношениями
Xw (X) =(dF (X))/dX ; F (X)= w (X) dX
-
справедливо выражение
w (X) = lim ((F(X+X)-F (X))/X)= lim ((Sd [[x(t) ,X]])/X)
X X
1 при X X+X
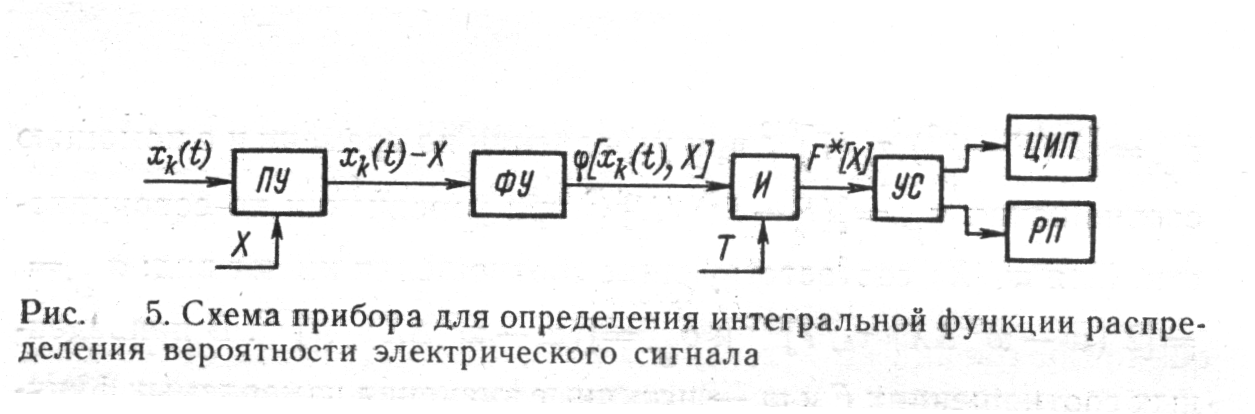
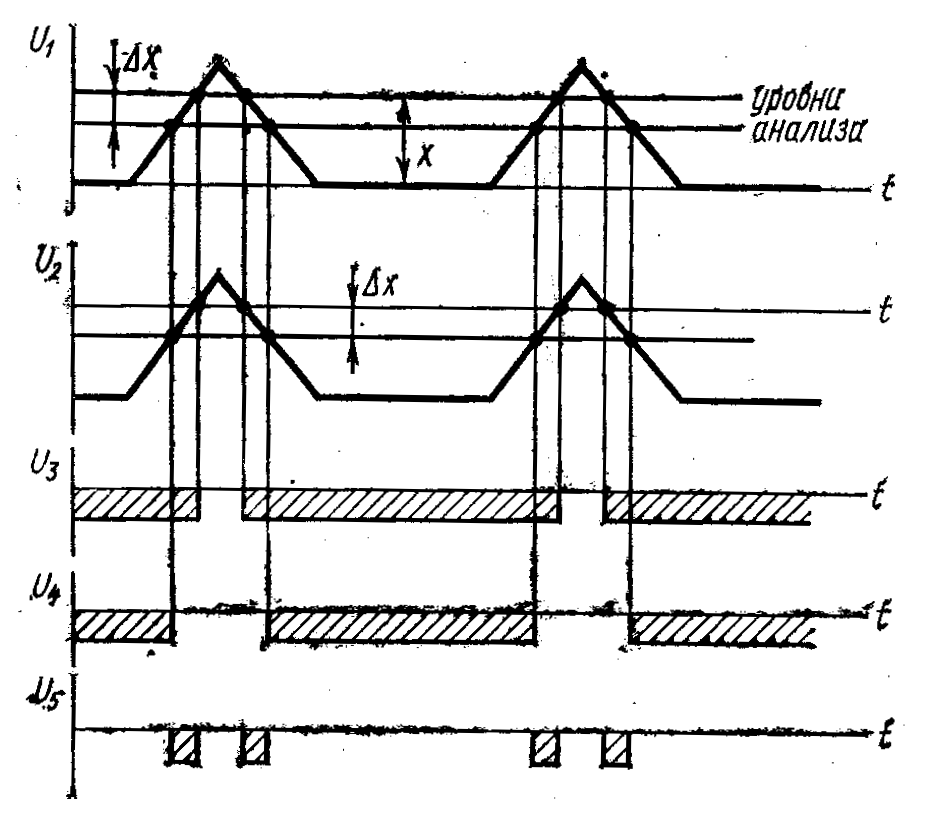
В качестве примера рассмотрим средство измерений для определения интегральной функции распределения вероятности уровня электрического сигнала. Схема средства измерений, реализующего алгоритм
t
F* (X)=1/T [xk(t) ,X]dt ,
t-T
показана на рис. 5, где ПУ — пороговое устройство, формирующее сигнал X k (t}—X; ФУ—формирующее устройство; И—интегратор, на выходе которого получается сигнал F* (X) при установленных значениях Х и Т; УС — устройство сопряжения;
ЦИП — цифровой прибор; РП — регистрирующий прибор.
Средняя квадратическая погрешность из-за конечности объема выборки определяется для F {X) с помощью соотношения
2 1/2
=[2(F - F ) k/T]
F
при усреднении по времени и с помощью соотношения
2 1/2
=[2(F - F )/N]
F
при усреднении по совокупности. Для (X) соответствующие соотношения имеют вид:
2 1/2
=[2(w - w X) k/T]
w
2 1/2
и =[(w - w X)/N]
w
В приведенных соотношениях F и w — истинные значения измеряемых функций при данном X.
4. ИЗМЕРЕНИЯ КОРРЕЛЯЦИОННОЙ ФУНКЦИИ
Для случайного процесса с нулевым математическим ожиданием корреляционная функция равна:
Rx (s,) = lim Sd[xi (t) xi-s (t-)],
d
где и s — соответственно сдвиг во времени и в пространстве реализации перемножаемых мгновенных значений.
В практических задачах большую роль играют стационарные случайные процессы, т. е. процессы с постоянными вероятностными характеристиками, не зависящими от текущего времени. Среди случайных процессов можно выделить эргодические процессы, для которых
t
Rx () = lim 1/T x (t) x (t-)dt,
T 0
Большое значение корреляционного анализа в различных областях науки и техники привело к созданию множества измерительных приборов для измерений корреляционных функций — коррелометров.
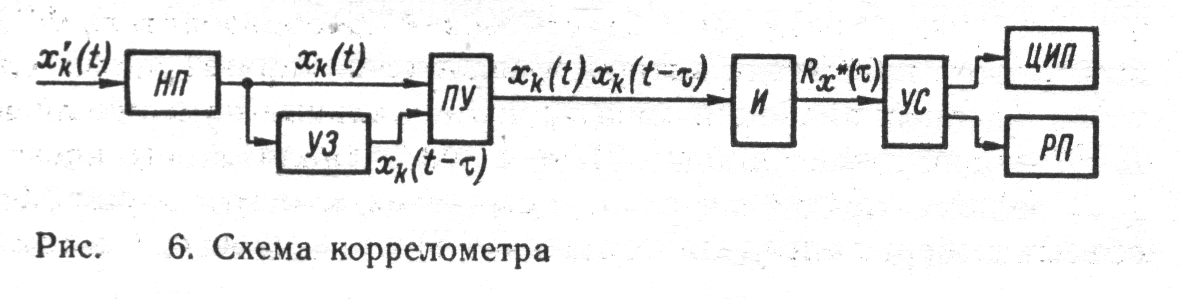
Типовая структура коррелометра, в котором используется усреднение по времени, представлена на рис. 6. При этом реализуется следующий алгоритм:
t
R*x () = 1/T xk (t) xk (t-)dt,
t-T
Как видно, после нормирующего преобразователя НП сигнал поступает в устройство временной задержки УЗ и на перемножающее устройство ПУ, осуществляющее перемножение мгновенных значений, сдвинутых по времени на интервал т. Далее с помощью интегратора И выполняется усреднение, после которого результирующий сигнал через УС подается на цифровой прибор ЦИП или регистрирующий прибор РП.
Средние квадратические погрешности, обусловленные конечностью объема выборочных данных о мгновенных значениях реализации процесса Х (t), оцениваются с помощью соотношений:
1/2
={2D[xk (t) xk (t-)] k/T}
R
при усреднении по времени Т и
1/2
={D[xk (t) xk (t-)]/N}
R
при усреднении по совокупности.
5. АНАЛИЗ СПЕКТРА МОЩНОСТИ
Спектр мощности характеризует ее частотное распределение, и он может быть определен в соответствии со следующими формулами:
2
Sx(w) = lim 1/T xiT (w)
T
Где
t -jwt’
XiT (w) = xi (t’) e dt’
t-T
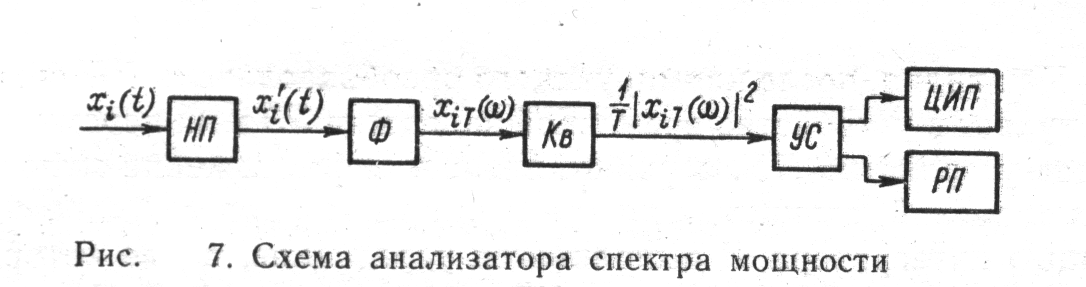
На рис. 7 изображена схема анализатора спектра мощности случайного процесса Х (t).
С выхода нормирующего преобразователя НП i-я реализация случайного процесса xi (t) поступает на блок Ф, выполняющий преобразование Фурье, после чего узлом Кв производится возведение в квадрат и нормирование с учетом интервала усреднения Т. С помощью устройства сопряжения УС сформированный сигнал поступает на ЦИП и регистратор РП.
В настоящее время отечественной промышленностью серийно выпускаются анализаторы случайных процессов. К ним относятся многофункциональный статистический преобразователь Ф790, корреллометр Ф7016, комплекс измерителей характеристик случайных сигналов Х6-4/а, многофункциональные измерители вероятностных характеристик Ф36 и Ф37, анализаторы спектра Ф4326, Ф4327, Ф7058 и др. С помощью этих приборов и устройств можно измерять математические ожидания и дисперсии, а также значения функций распределения вероятности, корреляционных и спектральных функций с последующим восстановлением вида самих функций. Перечисленные анализаторы рассчитаны в основном на унифицированный входной сигнал и позволяют измерить от 256 до 4096 ординат анализируемой функции. Погрешность измерения не превышает ±5 %.
Кроме того, для определения вероятностных характеристик случайных сигналов могут использоваться электроизмерительные приборы, предназначенные для измерения среднего и действующего значений сигнала. Для определения среднего значения применяют магнитоэлектрические приборы и цифровые интегрирующие приборы. Для определения среднего квадратического отклонения используют приборы, показания которых определяются действующим значением сигнала (термоэлектрические, электростатические и др.).
Корреляционные устройства получили применение в различных областях науки и техники для измерения различных величин. В качестве примера можно указать корреляционное устройство для измерения скорости прокатки. Эти устройства измеряют корреляционную функцию, зависящую от т, которая, в свою очередь, зависит от скорости прокатки.
Список литературы :
1.Метрология и электроизмерительные приборы. Душин М .Е.\М.: Энергоатомиздат,1986.
2.Метрология, стандартизация и измерения в технике связи. Под ред. Б.П. Хромого
М.: Радио и связь, 1986.
3.Основы метрологии и стандартизации. Голубева В. П. \М .: Вектор, 19
Похожие работы
... математического ожидания. Таким образом, (72.6) принимает вид . (72.7) 72.2. Функции вида , (72.8) где целые числа , называются начальными моментами порядка случайного процесса . Аналогично центральные моменты определяются соотношениями: . (72.9) Для функций (72.8), (72.9) используется общее название - моментные функции. Наиболее простые ...
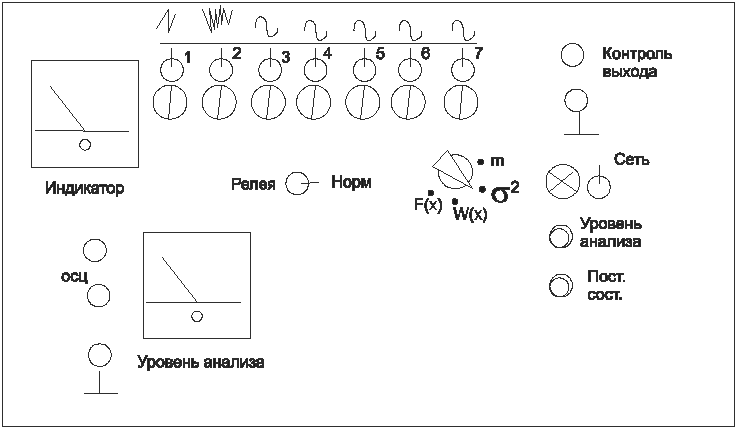
... функция и функция плотности и вероятности имеют следующий вид: Описание лабораторной установки Для выполнения работы необходимо использовать универсальный стенд для изучения законов распределения случайных процессов и электронный осциллограф. Передняя панель стенда Стенд включает в себя: - семь источников независимых случайных сигналов (одного шумового с нормальным распределением, ...
... как . Найдем явный вид коэффициентов в представлении (2.4), Видим, что Таким образом, справедливо следующее утверждение. Теорема 2.1. Оценка взаимной спектральной плотности стационарного в широком смысле случайного процесса , задаваемая равенством (2.5), удовлетворяет соотношению , , при условии, что справедливо соотношение (2.4) для При нахождении моментов оценок ...
... 5), в котором предусмотрена возможность усреднения (Averaging) и оконной обработки (Window) для уменьшения краевых эффектов. а) б) Рис. 5 2. Генерирование коррелированных случайных последовательностей Чаще всего для генерирования коррелированных случайных последовательностей используется метод формирующего фильтра. Если на вход линейного формирующего фильтра подать белый шум x(t), ...
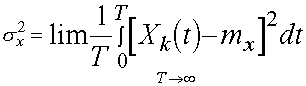

0 комментариев