Навигация
2.2. Синтез блока С
В блоке С выделено несколько полей, соответственно синтез будет производиться для каждого из них отдельно.
Поле С(1).
y1:
С(1):=0
Таблица и функции аналогичны таблице 5 и функциям для микрооперации y1 над полем П(1).
J=0, K=1.
y2:
С(1):=P(1), где P(1) – перенос в первый разряд из второго.
Так как р поле С(1) было обнулено при микрооперации y1, то в таблице 7 можно рассматривать только наборы, где С(1)=0.
Таблица 7
| t | t+1 | t | ||
| С(1) | P(1) | С(1) | J | K |
| 0 | 0 | 0 | 0 | 0Ú1 |
| 0 | 1 | 1 | 0Ú1 | 1 |
Дополнив функцию на невозможных наборах, получаются следующие выражения функций возбуждения.
J=P(1),
K=1.
Функция P(1) будет найдена при синтезе поля С(2), так как она зависит от значения самого поля, переноса в этот разряд и значения слагаемых, сумма которых записывается в разряд С(2).
y3:
В этой микрооперации все аналогично таблице 7, то есть
J=P(1), K=1.
y6:
С(1):=0
Таблица переходов аналогична таблице 5, значит сразу известны выражения для J и K.
J=0, K=1.
y4:
C(1):=C(1)+P(1)
![]()
J=P(1)
K=P(1)
Окончательный результат синтеза поля С(1) может быть представлен в виде:
![]()
Логическое условие:
x3=С(1).
Логическая схема поля С(1) будет выглядеть так, как это показано на рис. 2.2.1.
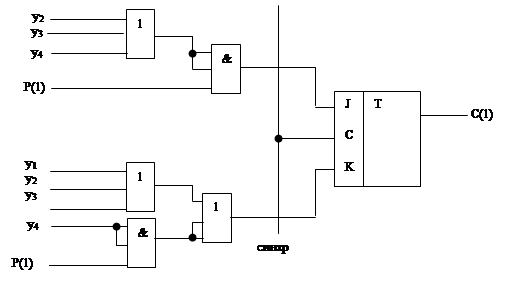
Рис. 2.2.1.
Данной схеме можно сопоставить условное изображение "черного ящика", то есть известно, что на входе и, что на выходе. Эта схема представлена на рисунке 2.2.2.
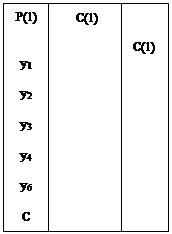
Рис. 2.2.2.
Поле С(2).
y2:
С(2):=1+P(2)
Можно перейти к булеву выражению этого разряда
С(2)=![]()
Соответственно таблица функций (табл. 8) возбуждения будет выглядеть так:
Таблица 8
| T | t+1 | t | |||
| С(2) | P(2) | С(2) | P(1) | J | K |
| 0 | 0 | 1 | 0 | 1 | 0Ú1 |
| 0 | 1 | 0 | 1 | 0 | 0Ú1 |
| 1 | 0 | 1 | 0 | 0Ú1 | 0 |
| 1 | 1 | 0 | 1 | 0Ú1 | 1 |
Из данной канонической таблицы необходимо написать выражения функций J, K, P(1).
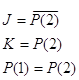
y3:
Абсолютно аналогично y2:
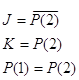
y6:
С(2):=P(2)
Соответственно таблица функций (табл. 9) возбуждения будет выглядеть так:
Таблица 9
| T | t+1 | t | |||
| С(2) | P(2) | С(2) | P(1) | J | K |
| 0 | 0 | 0 | 0 | 0 | 0Ú1 |
| 0 | 1 | 1 | 0 | 1 | 0Ú1 |
| 1 | 0 | 0 | 0 | 0Ú1 | 1 |
| 1 | 1 | 1 | 0 | 0Ú1 | 0 |
Из данной канонической таблицы необходимо написать выражения функций J, K, P(1).
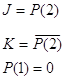
y8:
С(2):=А(1)
Таблица аналогична таблице 9, только столбец P(2) заменяется на А(1). А функции выглядят так:
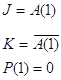
y4:
C(2):=C(2)+P(2)
![]()
J=P(2)
K=P(2)
P(1)=P(2)C(2)
Составляются результирующие функции возбуждения элемента памяти и переноса в старший разряд, а также выражение функции логического условия.
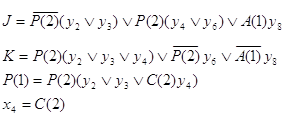
Выражение для P(2) будет найдено при синтезе поля С(3:25).
|
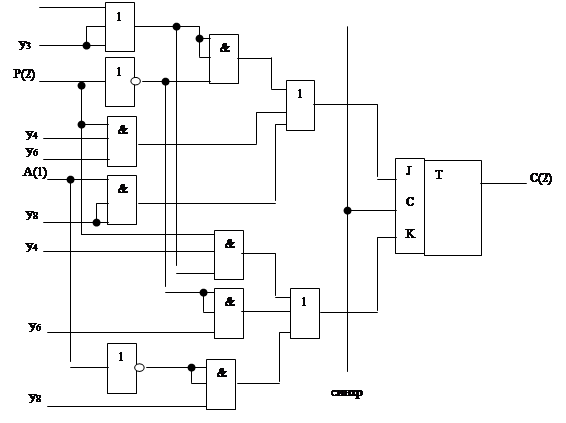
Рис. 2.2.3.
На рис. 2.2.4. представлено условное обозначение разряда С(2).
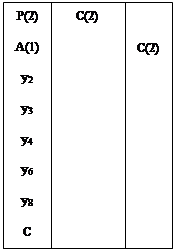
Рис. 2.2.4.
|

Рис. 2.2.5.
Поле С(3:25).
Здесь для синтеза можно выбрать любой разряд этого поля, и обозначить его как С(i).
y2:
C(i):=ùA(i-1)+B(i-1)+P(i)
В виде логической функции это получится так,
![]() , здесь P(i) перенос в i-ый разряд
, здесь P(i) перенос в i-ый разряд
Примечание.
Следует заметить, что выражение для переноса P(i) будет выглядеть совершенно идентично выражению для P(2) и P(i-1), в таком случае можно ограничится синтезом только P(i-1).
Составляется каноническая таблица переходов для поля C(i) (табл. 10)
Таблица 10
| t | t+1 | t | |||||
| C(i) | A(i-1) | B(i-1) | P(i) | C(i) | P(i-1) | J | K |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0Ú1 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0Ú1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0Ú1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0Ú1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0Ú1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0Ú1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0Ú1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0Ú1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0Ú1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0Ú1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0Ú1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0Ú1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0Ú1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0Ú1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0Ú1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0Ú1 | 1 |
Составляются функции возбуждения и функция переноса P(i-1) из таблицы 10:
J
| B(i-1)P(i) C(i)A(i-1) | 00 | 01 | 11 | 10 |
| 00 | 1 | 0 | 1 | 0 |
| 01 | 0 | 1 | 0 | 1 |
| 11 | * | * | * | * |
| 10 | * | * | * | * |
K
| B(i-1)P(i) C(i)A(i-1) | 00 | 01 | 11 | 10 |
| 00 | * | * | * | * |
| 01 | * | * | * | * |
| 11 | 0 | 1 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
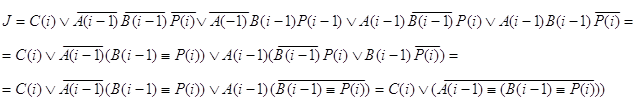
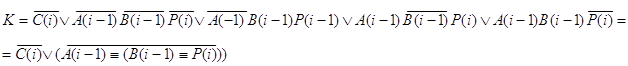
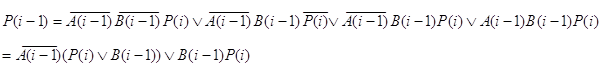
y3:
C(i):=A(i-1)+ùB(i-1)+P(i),
![]()
Аналогично y2 с заменой в табл. 10 столбца A(i-1) на B(i-1), а B(i-1) на A(i-1), соответственно получается:
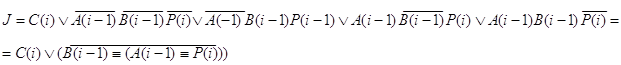
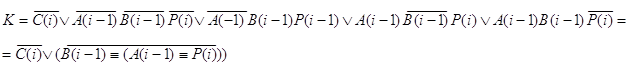
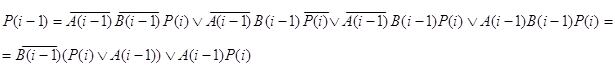
y5:
C(i):=ùC(i), необходимо перейти к выражению в виде булевой функции,
![]()
Таблица функций возбуждения триггера (табл. 11) будет выглядеть так,
Таблица 11
| T | t+1 | t | |
| C(i) | C(i) | J | K |
| 0 | 1 | 1 | 0Ú1 |
| 1 | 0 | 0Ú1 | 1 |
Из таблицы 11 можно написать выражения для J и K.
J=1
K=1
y6:
C(i):=A(i-1)+B(i-1)+P(i), переход к булевой функции,
![]()
Составляется каноническая таблица функций возбуждения (табл. 12),
Таблица 12
| t | t+1 | t | |||||
| C(i) | A(i-1) | B(i-1) | P(i) | C(i) | P(i-1) | J | K |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0Ú1 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0Ú1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0Ú1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0Ú1 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0Ú1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0Ú1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0Ú1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0Ú1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0Ú1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0Ú1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0Ú1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0Ú1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0Ú1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0Ú1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0Ú1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0Ú1 | 0 |
Составляются функции возбуждения и функция переноса P(i-1) из таблицы 12:
J
| B(i-1)P(i) C(i)A(i-1) | 00 | 01 | 11 | 10 |
| 00 | 0 | 1 | 0 | 1 |
| 01 | 1 | 0 | 1 | 0 |
| 11 | * | * | * | * |
| 10 | * | * | * | * |
K
| B(i-1)P(i) C(i)A(i-1) | 00 | 01 | 11 | 10 |
| 00 | * | * | * | * |
| 01 | * | * | * | * |
| 11 | 1 | 0 | 1 | 0 |
| 10 | 0 | 1 | 0 | 1 |
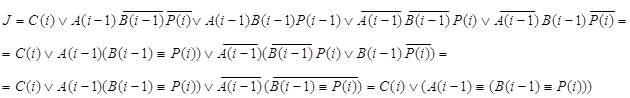
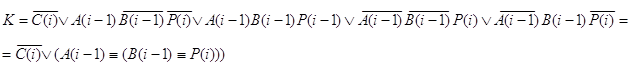
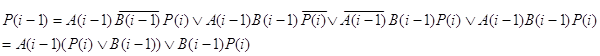
y4:
C(i):=C(i)+P(i)
![]()
J=P(i)
K=P(i)
P(i-1)=C(i)P(i)
Составляются результирующие функции J, K и P(i-1), по ним на рис. 2.2.6., рис. 2.2.7. изображены логические схемы C(i), P(i-1), а на рис. 2.2.8. и рис. 2.2.9. соответственно даны их условные обозначения.
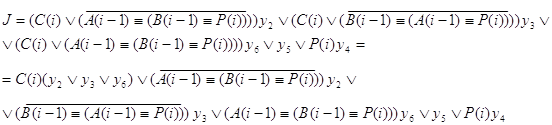
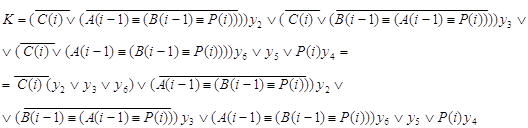
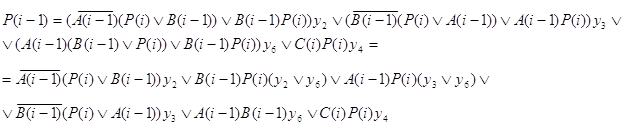

Рис. 2.2.6.
![]()
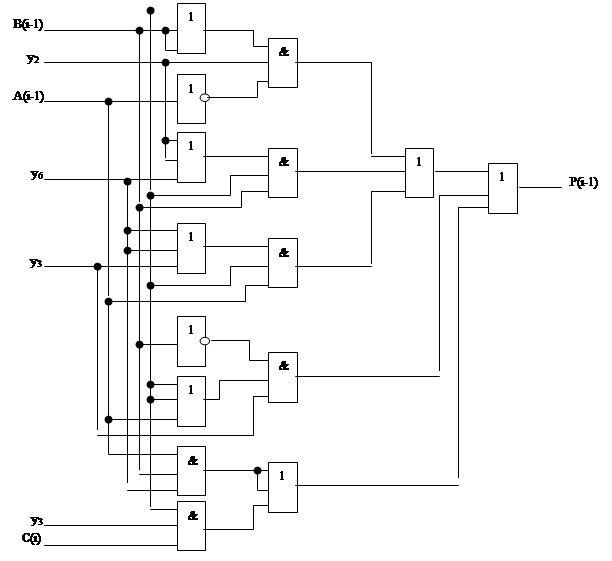
Рис. 2.2.7.

Рис. 2.2.8.
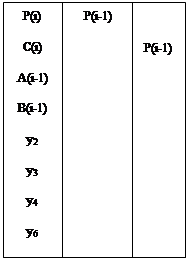
Рис. 2.2.9.
Поле С(26).
y2:
C(26):=ùA(25)+B(25)
В виде логической функции это получится так,
![]() ,
,
Составляется таблица 13 функций возбуждения элементов памяти, по этой таблице будет так же определяться функция переноса P(25).
Таблица 13
| t | t+1 | t | ||||
| C(26) | A(25) | B(25) | C(26) | P(25) | J | K |
| 0 | 0 | 0 | 1 | 0 | 1 | 0Ú1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0Ú1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0Ú1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0Ú1 |
| 1 | 0 | 0 | 1 | 0 | 0Ú1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0Ú1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0Ú1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0Ú1 | 0 |
Составляются функции:
J
| А(25)В(25) С(26) | 00 | 01 | 11 | 10 |
| 0 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 |
K
| А(25)В(25) С(26) | 00 | 01 | 11 | 10 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 |
![]()
![]()
![]()
y3:
C(26):= A(25)+ ùB(25)
В виде логической функции это получится так,
![]() ,
,
Аналогично таблице 13 с заменой столбцов А(25) на В(25) и В(25) на А(25).
![]()
![]()
![]()
y4:
С(26):=С(26)+1,
![]()
Таблица идентична таблице 11, соответственно функции имеют вид,
J=1, K=1, P(25)=C(26).
y5:
С(26):=ùС(26),
![]()
Таблица идентична таблице 11, соответственно функции имеют вид,
J=1, K=1.
y2:
C(26):=A(25)+B(25)
В виде логической функции это получится так,
![]() ,
,
Составляется таблица 14 функций возбуждения элементов памяти, по этой таблице будет так же определяться функция переноса P(25).
Таблица 14
| t | t+1 | t | ||||
| C(26) | A(25) | B(25) | C(26) | P(25) | J | K |
| 0 | 0 | 0 | 0 | 0 | 0 | 0Ú1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0Ú1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0Ú1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0Ú1 |
| 1 | 0 | 0 | 0 | 0 | 0Ú1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0Ú1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0Ú1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0Ú1 | 1 |
Составляются функции:
J
| А(25)В(25) С(26) | 00 | 01 | 11 | 10 |
| 0 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 |
K
| А(25)В(25) С(26) | 00 | 01 | 11 | 10 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 |
![]()
![]()
![]()
Составляются результирующие функции J, K и P(25), по ним на рис. 2.2.10., рис. 2.2.11. изображены логические схемы C(26), P(25) соответственно, а на рис. 2.2.12. и рис. 2.2.13. соответственно даны их условные обозначения.
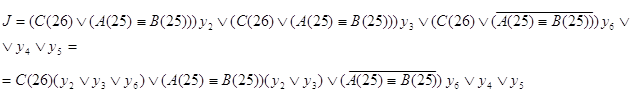
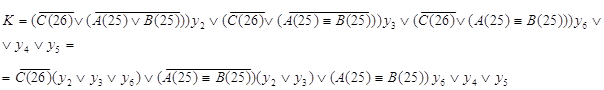
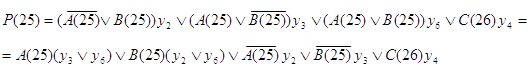
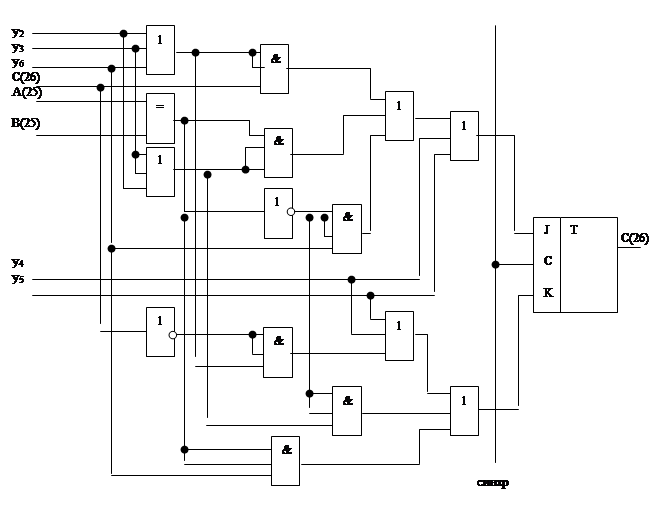
Рис. 2.2.10.
|
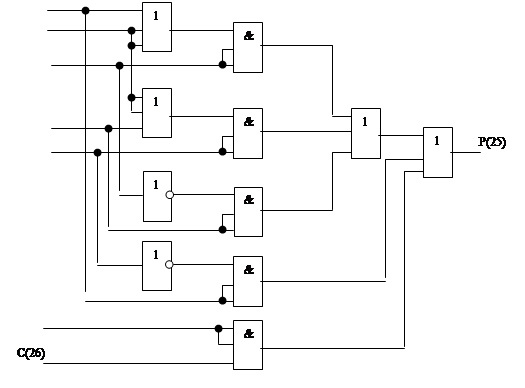
Рис. 2.2.11.
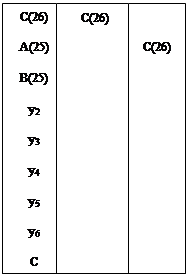
Рис. 2.2.12.

Рис. 2.2.13.
3.Разработка функциональной схемы управляющего автомата
Похожие работы
... лекций. Основное внимание при выполнении курсового проекта обращается на умение принимать технические решения и обосновывать их. Объектом курсового проектирования является специализированное вычислительное устройство, включающее процессор и запоминающее устройство. Процессор проектируется для заданного списка команд и должен удовлетворять заданным требованиям технического задания. 2.Задание ...
... литературе как "рабочая станция" (PC). Рис. 3. Структура рабочей станции проектирования электронных систем. Рис. 4. Структура ПО САПР. 4. Иерархические уровни представления электронных устройств Основным методом проектирования с применением САПР является блочно-иерархический метод или метод декомпозиции сложного объекта на подсистемы (блоки, узлы, компоненты). В этом случае ...
... же порты ввода-вывода или линии запроса прерывания. С такими проблемами, как конфликты различных частей аппаратуры, приходится иметь дело в основном именно операционным системам. Наконец, в-восьмых, при разработке операционных систем часто учитывается необходимость совместимости с предыдущей версией операционной системы. Система может иметь множество ограничений на длину слов, имена файлов и т. ...
... операционный баланс будет равен суточному балансу. Производительность проектируемого производства составляет 13 тонн/год. Предполагается, что проектируемое производство будет работать 237 дней в году. Из этих данных определяем суточную производительность проектируемого объекта: т готовой динитробензойной кислоты. Таблица №12 Операционный материальный баланс стадии нитрования Приход кг ...


0 комментариев