Навигация
Методы определения первоначального опорного плана
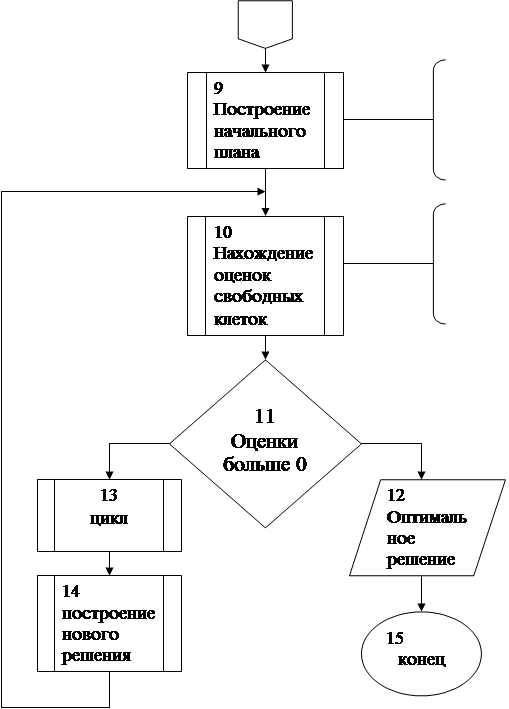
4. Методы определения первоначального опорного плана
4.1. Метод минимального элемента
Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел ![]() и
и ![]() . Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
. Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
Пример
Составить первоначальный опорный план методом минимального элемента для транспортной задачи вида:
| 2 | 3 | 4 | 15 |
| 11 | 6 | 10 | 1 |
| 8 | 9 | 3 | 3 |
| 4 | 1 | 2 | 21 |
| 10 | 20 | 10 |
Решение:
Задача сбалансирована.
Строим первоначальный опорный план методом минимального элемента.
Выясним минимальную стоимость перевозок.
6. Шестая перевозка осуществляется с пункта ![]() в пункт потребления
в пункт потребления ![]() т.к.
т.к. ![]() (без учета первого, второго столбца, первой, третьей и четвертой строки).
(без учета первого, второго столбца, первой, третьей и четвертой строки). ![]()
Опорный план имеет вид;
| 10 | 5 | 0 |
| 0 | 1 | 0 |
| 0 | 3 | 0 |
| 0 | 11 | 10 |
Похожие работы
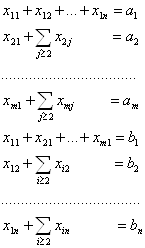
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... , является линейной функцией переменных : (2.4) Требуется в области допустимых решений системы уравнений (2.1) и (2.1.1) найти решение, минимизирующее линейную функцию (2.4). Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без ...
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
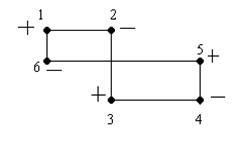
... . Система векторов условий транспортной задачи линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимое решение транспортной задачи , i=1,2,…,m; j=1,2,…,n является опорным только в том случае, когда из занятых им клеток таблицы нельзя образовать ни одного цикла. Метод вычеркивания. Для проверки возможности ...





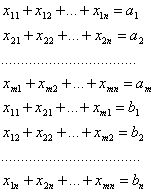



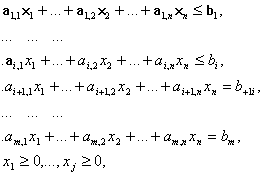
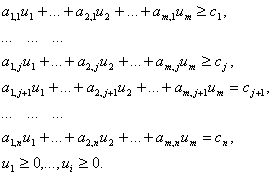
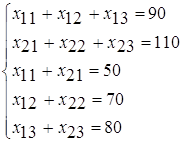
0 комментариев