Навигация
Методы алгебраических и дифференциальных уравнений для анализа и качественного исследования социально-экономических явлений (По дисциплине: Математические методы моделирования процессов управления в социальной сфере)
Санкт-Петербургский Государственный Технический Университет
Гуманитарный факультетКафедра социологии и права
РЕФЕРАТ
На тему : Методы алгебраических и дифференциальных уравнений для анализа и качественного исследования социально-экономических явлений.
По дисциплине: Математические методы моделирования процессов управления в социальной сфере
Выполнил :
Студент Кириллова Н.В.
Группы 5121/1Проверил:
Руководители Романов М.Ф. Максимов Ю.Д.Санкт-Петербург
2000 г.
ВВЕДЕНИЕ
Рынок представляет собой систему саморегулирования экономики по таким параметрам, как величина покупательного спроса, качество продукции, общественно необходимые затраты труда, объем производства товаров и услуг. Механизм саморегулирования включает в себя свободные рыночные цены, экономическую конкуренцию между производителями, свободный выбор деловых партнеров.
Регулирование рынка со стороны центра осуществляется с помощью экономических рычагов - таких, как налоговая, финансовая и кредитная политика, цены на отдельные группы товаров, система дотаций и социальной защиты человека. В процессе регулирования рынка должны учитываться экономические интересы как производителей, так и потребителей.
Естественно, что для описания некоторых элементов рыночного механизма используются простейшие математические модели. Такие модели отображают только самые общие свойства экономических систем. В данной работе приводится способ исследования социально-экономических явлений путем составления алгебраических и дифференциальных уравнений.
1. Простейшая модель изменения зарплаты и занятости
Характерная черта рыночной системы хозяйства - наличие рынка труда, на котором взаимодействуют работодатели и наемные рабочие. Пусть все участники рынка труда располагают на этом рынке одинаковой информацией в одинаковом объеме и принимают на основе этой информации наилучшие, оптимальные для себя решения. Взаимодействие спроса и предложения на этом цивилизованном рынке приводит к равновесию, при котором за плату' p > 0 согласны работать N > 0 человек. Если по каким-то причинам это равновесие со временем нарушается (например, часть работников уходит на пенсию по возрасту, либо у работодателя возникают финансовые трудности), то функции P(t) и N(t) отклоняются от р ,N .
Функции P(t) и N(t) рассматриваются как непрерывные и достаточно гладкие. Эти условия принимаются исключительно из соображений, связанных с математическими действиями, основывающимися на свойствах достаточно гладких решений.
Будем считать, что число работников увеличивается или уменьшается пропорционально росту или уменьшению зарплаты относительно значения p .
Тогда
(1)
Предположим, что работодатели изменяют зарплату также пропорционально отклонению численности занятых от равновесного значения n ,т. е.
(2)
Дифференцируя равенство (1) по t, получим d N/dt2 = a dP/dl. Из этого равенства в силу (2) следует d N/dt -= -a a (N - n ), откуда
(3)
Общее решение уравнения (3), имеет вид
(4)
где C и С - произвольные постоянные.
Из (1) в силу (4) получаем(5)
Умножим уравнения (4), (5) соответственно на и , возведем затем в квадрат левые и правые части получившихся равенств. После сложения левых и правых частей будем иметь
(P-P )2+ (N-No) 2=const>0. (6)
Рассматривая значения переменных N, Р как координаты точки на плоскости, можно геометрически представить состояние рынка посредством точки M(N,P). Эту точку в теории дифференциальных уравнений называют фазовой точкой, а плоскость ONP, на которой интерпретируется решение (6), - фазовой плоскостью. Решение (3), (4) представляет собой некоторый закон движения точки M(N,P) на фазовой плоскости.
Из графика кривой (6) видно (рис. 1), что при различных значениях const мы будем получать различные эллипсы с центром в точке (n , P ), отвечающие соответствующим начальным условиям N и Р.
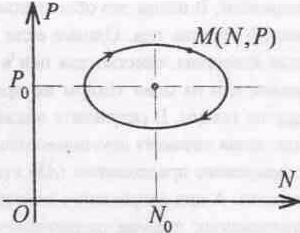
Рис 1.
Соотношение между зарплатой (Р) и числомработников (N) при нарушении равновесия.
Точка M(N,P), находящаяся на эллипсе, опишет за конечное время замкнутую кривую и за время t=2 / возвратится в свое начальное положение, возобновив то же самое движение. Следовательно, имеется периодичность с периодом 2 / .
Из уравнения (6) видно (см. также рис. 1), что в некоторые моменты времени t, когда N = N (т. е. когда число занятых становится равным равновесному значению), имеем Р>Р , т.е. зарплата превышает равновесную, а при Р = p получаем N > n , т. е. число занятых больше равновесного. В эти моменты фонд заработной платы, равный PN, превышает равновесное значение PoNo или меньше его). Но в среднем за период колебаний величина PN , равна PoNo .
Замечание. Построенная модель основана на правдоподобных представлениях о характере взаимодействия работодателя и наемных рабочих.
Похожие работы
... . В XVIII в. из математического анализа выделился ряд важных математических дисциплин: теория дифференциальных уравнений, вариационное исчисление. В это время началась разработка теории вероятностей. 3. Развитие математики в России в XVIII-XIX столетиях Математическое образование в России находилось в 9—13 веках на уровне наиболее культурных стран Восточной и Западной Европы. Затем оно ...
... Возникшие потребности в научно обоснованных методах и средствах управления нашли свое выражение в кибернетике - науке об управлении и системном анализе, особым предметом исследования которых являются сложные и очень сложные системы окружающего мира. 4.4 Организационные системы Традиционно современная кибернетика рассматривала, в основном, простые и сложные управляемые системы, для которых ...
... при финансовой поддержке государственной научно-технической программы «Физика квантовых и волновых процессов» (проект 1.61) и физического учебно-научного центра «Фундаментальная оптика и спектроскопия». 1. Асимптотическое поведение решений дифференциальных уравнений с малым параметром Многие колебательные системы описываются дифференциальными уравнениями с малым параметром при производных: ...
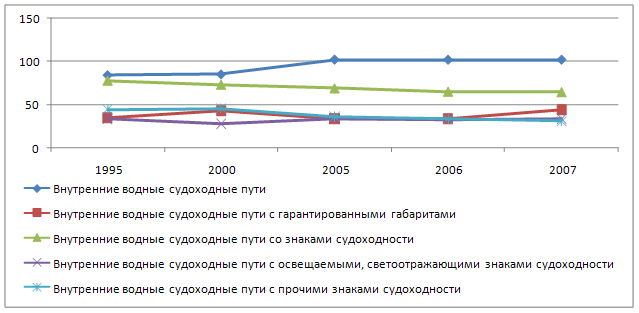
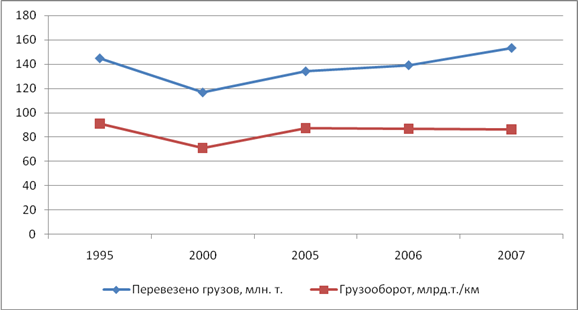
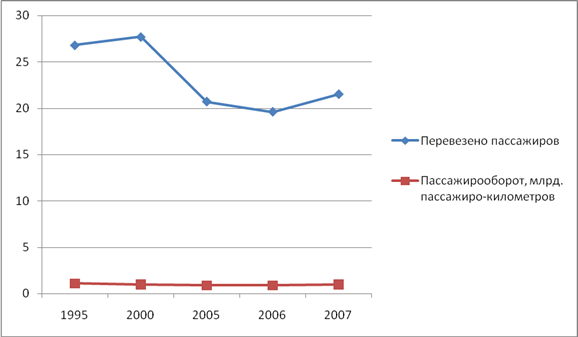
... , а в предыдущие периоды происходило снижение. Таким образом, по результатам проведенного анализа мы видим ухудшение основных показателей деятельности внутреннего водного транспорта в РФ. 2.2 Оценка структуры и динамики структуры экономико-статистических показателей внутреннего водного транспорта Далее проведем анализ структуры и динамики структуры основных показателей развития внутреннего ...



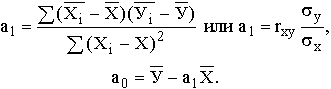
0 комментариев