Навигация
Класс Т – цирковая кличка собаки Каштанки, (Тетка);
5 класс Т – цирковая кличка собаки Каштанки, (Тетка);
Р – полевой цветок народный для гадания пригодный, (ромашка);
О – время года, когда листья становятся разноцветными, (осень);
З – свет мой... скажи, да всю правду расскажи, (зеркальце);
Е – самая плохая оценка (7 букв), (единица);
К – и от дедушки ушел, и от бабушки ушел, (Колобок);
О – металл, из которого сделан стойкий солдатик, (олово);
Из первых букв оставляем слово-анаграмму – ОТРЕЗОК. 7 класс – геометрия О – видит... да зуб неймет, (око);
В – перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону треугольника, (высота);
С – вездеход Бабы Яги, (ступа);
Й – последняя буква в названии липкой жидкости, которой можно соединить бумагу, (клей);
Т – угол, градусная мера которого больше 90°, (тупой);
О – название второй координатной точки, (ордината);
В – город, в пригороде которого стоит храм Покрова на Нерли, (Владимир);
С – восточная точка Африки, (Сафун).
Получается слово – СВОЙСТВО. 9 класс – алгебра О – суша посреди моря, (остров);
П – параллелограмм, у которого диагонали равны, (прямоугольник);
З – утренняя трапеза, (завтрак);
А – домашний бассейн для рыб, (аквариум);
Е – детский юмористический журнал, (Ералаш);
К – английский писатель, которому обязан своей всемирной известностью Маугли, (Киплинг);
А – математическое предложение, принимаемое без доказательств, (аксиома);
Ь – буква, превращающая геометрическую фигуру в топливо, (угол – уголь);
Л – царствующая особа из земноводных, (лягушка);
Т – четырехугольник, у которого только две противоположные стороны параллельны, (трапеция).
Получаем слово – ПОКАЗАТЕЛЬ.
Числовой диктант7-й класс: Сумму смежных углов разделите на количество сторон квадрата. Возведите в квадрат количество букв в названии математического предложения, которое принимается без доказательства. К количеству букв в слове, которое обозначает немилость, наказание, прибавьте 2% от 550 (опала – 5 букв;
5 + 11 = 16). Количество материков умножьте на количество океанов (6*4 = 24). Количество признаков равенства треугольников умножьте на порядковый номер ноты «ля» в октаве (3*6 = 18). Из количества букв восьмого месяца в году вычтите количество букв в названии корневой системы у семейства сложноцветных (август – 6 букв; стержневая – 10; 6 – 10 = – 4). Найдите сумму цифр года Полтавской битвы. Данный прием фронтальной работы на уроке описан в «Математике», 1999, № 28 (приложение к газете «Первое сентября»).
Цифровой диктант
Тема «Решение уравнений» (5 класс) 1. Уравнение – это равенство, содержащее букву, значение которой надо найти. (1)
2. Чтобы найти неизвестное слагаемое, надо к сумме прибавить известное слагаемое. (0)
3. Решить уравнение – значит найти все его корни (или убедиться, что корней нет). (1)
4. 100 : 4 = 20. (0)
5. Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое. (1)
6. Корнем уравнения называется значение буквы, при котором из уравнения получается верное числовое равенство. (1)
7. 120 больше 60 на 2. (0) 1.010.110 Тема «Многочлены» (7 класс) 1. Марсианская впадина находится в Тихом океане. (1)
2. Ромб – это параллелограмм, у которого равны диагонали. (0)
3. Подобные слагаемые – это слагаемые с одинаковыми буквенными множителями. (1)
4. Сумма двух отрицательных чисел есть число положительное. (0)
5. Крайняя северная точка Африки – Альмади. (0)
6. Произведение двух отрицательных чисел есть число положительное. (1)
7. В равнобедренном треугольнике углы при основании равны. (1)
8. За нотой «фа» идет нота «ре». (0) 10.100.110
Задания со сменой установки
Задание 1 (5 класс) 43 0 55 148 1812 1. Сколько всего чисел?
2. На каком месте стоит число, которое не является натуральным?
3. На каком месте стоит число, в записи которого цифра 1 стоит в разряде десятков?
4. Сложите 3-е и 5-е числа с конца.
5. Какое число стоит после нуля?
6. На каком месте стоит трехзначное число?
7. Какие цифры отсутствуют в ряду?
8. Назовите первое число.
9. Какому историческому событию соответствует последнее число?
Задание 2 (8 класс)
1. Сколько было четных чисел?
2. Сколько чисел делятся на 5 без остатка?
3. На каком месте стоит число, равное двум квартетам?
4. Каким по счету было число, соответствующее порядковому номеру месяца августа в году?
5. Какой месяц соответствует предпоследнему числу?
6. Результат деления первого числа на четвертое? (25 : 10 = 2,5) 6. Порядковый номер какого дня недели получится при умножении второго числа на третье? (Четверг. 16 : = 4.)
8. В скольких числах есть буква «д»? (В трех: 25, 16, 10.)
9. В какую букву надо вписать число семь, чтобы получилось последнее число (В ** 7 – восемь.)
Похожие работы
... интеллектуальных переживаний, являющихся также сильными побудителями познавательного интереса. Здесь возникают коллективные сопереживания, радость за успех товарища, стремление оказать ему помощь. Повышение интереса на уроках математики может достигаться следующим образом: 1) Обогащение содержания материалом по истории науки. 2) Решение задач повышенной трудности и нестандартных задач. 3) ...
... росту. Существует определенная взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике. Глава II Развитие познавательного интереса к урокам математики младших школьников средствами использования занимательных дидактических игр 2.1 Дидактические игры, их виды В отличие от других видов деятельности игра содержит цель в самой себе; ...
... уроки сказки, веселые задачи в стихах, математические загадки, сказочные задачи, математические сказки, задачи занимательного характера, головоломки, кроссворды и логические задачи способствуют активизации мыслительной деятельности учащихся на уроках математики, подтвердилась. Для себя лично я усвоила правило: "Не бери игру на урок, для того чтобы развлечься. Все на уроке должно быть логически ...
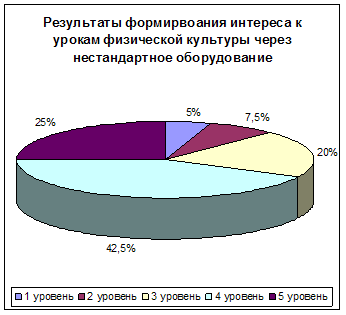
... у детей. Дети бережнее относится к инвентарю, повышается плотность урока, повышается качество обучения. Так же при использовании такого оборудования происходит влияние на формирование интереса младшего школьного возраста на уроках физической культуры. Происходит удовлетворение интереса, который может укрепляться, развиваться, становиться более глубоким и разносторонним. Интерес, таким образом, ...

0 комментариев