Навигация
Решение многокритериальной задачи линейного программирования графическим методом
2. Решение многокритериальной задачи линейного программирования графическим методом.
2.1.Формальное условие и сведение к ЗЛП
Чтобы можно было проверить условие (4) (Lr(x) Lr(x’),r) для некоторой произвольно взятой точки х,, не прибегая к попарному сравнению с другими, условие -оптимальности (4) переформулируем в виде следующей задачи линейного программирования:
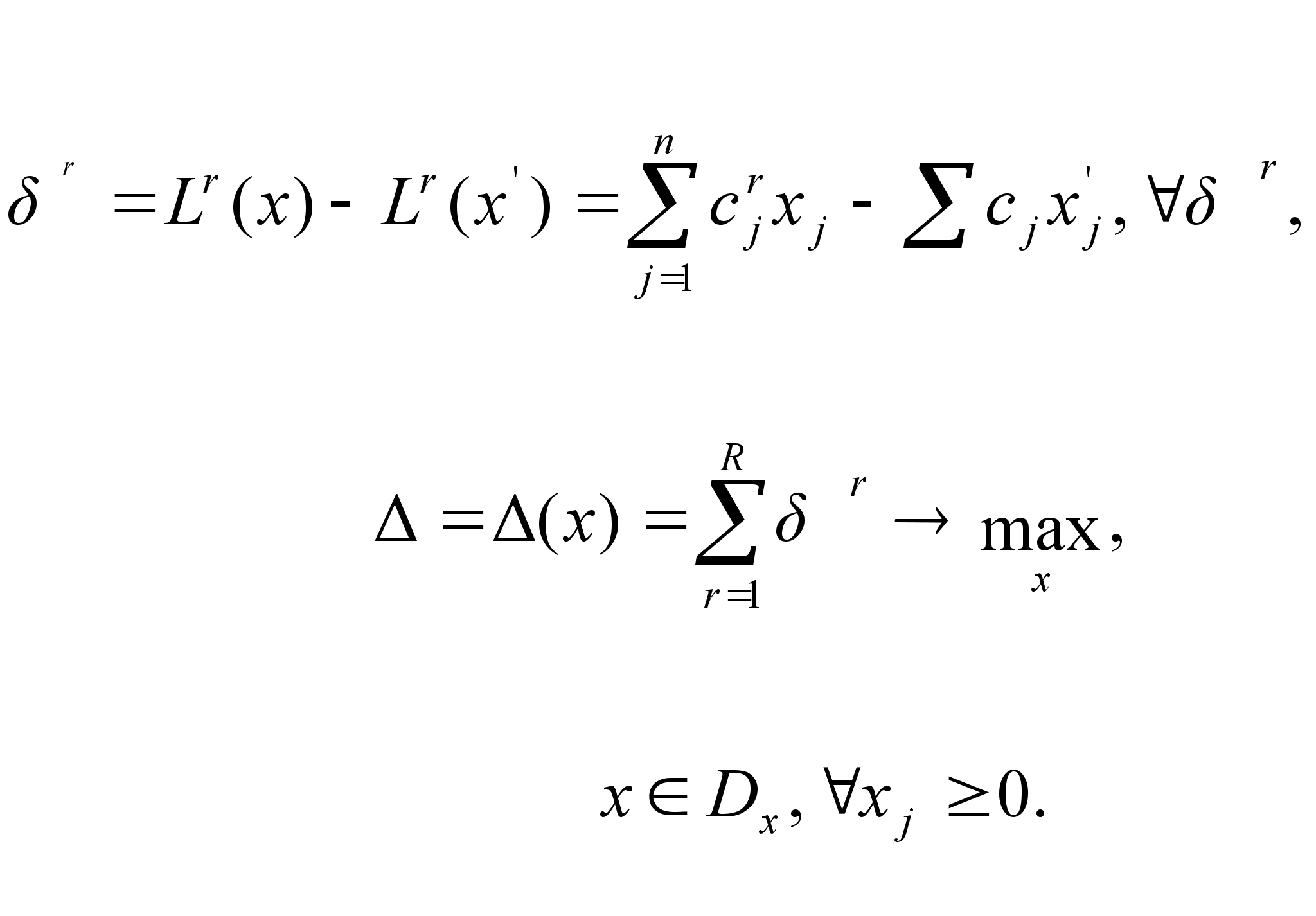
(5)
(6)
(7)
Смысл задачи линейного программирования нетрудно понять, если учесть, что r – это приращение ч-критерия Lr, получаемое при смещении решения х, в точку х. Тогда, если после решения ЗЛП окажется Dmax = 0, то это будет означать, что ни один из ч-критериев нельзя увеличить (Dmax = 0), если не допускать уменьшения любого из других ( r 0). Но это и есть условие -оптимальности х,. Если же при решении окажется, что 0, то значит какой-то ч-критерий увеличил свое значение без ухудшения значений других ( r 0), и значит х, Dx.
Теперь перейдем к решению нашей задачи:
L1 = -x1 + 2x2 + 2,
L2 = x1 + x2 + 4,
L3 = x1 - 4x2 + 20,
x1 + x2 15,
5x1 + x2 1,
-x1 + x2 5,
x2 20,
xj 0.
Проверим некоторую точку х, = (5; 3) (эта точка принадлежит области Dx) на предмет -оптимальности:
Запишем ЗЛП в каноническом виде:
![]() 1
= x1
- 2x2
+ 1
1
= x1
- 2x2
+ 1
Dxk 2 = x1 + x2 - 8
3 = -x1 + 4x2 - 7
= x1 + 3x2 – 14,
![]() 1
= 15 - x1
- x2
1
= 15 - x1
- x2
2 = 5x1 + x2 – 1,
Dx 3 = 5 + x1 - x2
4 = 20 - x2
xj 0.
и в форме с-таблицы:
| Т1 | х1 | х2 | 1 |
| 1 | -1 | -1 | 16 |
| 2 | 5 | 1 | -4 |
| 3 | 1 | -1 | 100 |
| | 0 | -1 | 10 |
| 1 | 1 | -2 | -4 |
| 2 | 1 | 1 | -12 |
| 3 | -1 | 1 | -8 |
| | 1 | 4 | -24 |
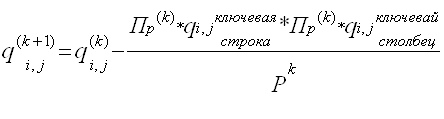
Применяя с-метод, после замены 3 х2, получаем:
| Т2 | х1 | 1 | 1 |
| 1 | -3/2 | Ѕ | 29/2 |
| 2 | 11/2 | -1/2 | -1/2 |
| 3 | 1/2 | Ѕ | 9/2 |
| 4 | -1/2 | Ѕ | 39/2 |
| X2 | 1/2 | -1/2 | 1/2 |
| 2 | 3/2 | -1/2 | -15/2 |
| 3 | 1 | -2 | -5 |
| | 5/2 | -3/2 | -25/2 |
Видим, что опорный план не получен, следовательно делаем еще одну замену: 1 х1:
| Т3 | 3 | 1 | 1 |
| x1 | 29/3 | ||
| 2 | 316/6 | ||
| 3 | 56/6 | ||
| 4 | 88/6 | ||
| x2 | 16/3 | ||
| 2 | 7 | ||
| 3 | 14/3 | ||
| | -5/3 | -2/3 | 70/6 |
В Т3 получен опорный план. Так как при этом >0, то, следовательно, система ч-критериев не противоречива и существует некоторая область, смещение в которую решения х, способно увеличить, по крайней мере, один ч-критерий без уменьшения значений остальных. Эта область и есть конус доминирования - д – конусом Dxk (на рисунке выделен штриховкой). При R > n д-конус может выродиться в точку х, (вершина д-конуса). Получено целое множество оптимальных решений, извлекаемое из Т3: х0 = ( 29/3 ; 16/3 ). Таким образом, решение х, = ( 5; 3) не является -оптимальным, так как его удалось улучшить (max>0). Помимо установления факта неэффективности решения х,, рассмотренный метод позволил определить ближайшее к нему -оптимальное решение.
Похожие работы
... = -x1 + 2x2 + 2, L2 = x1 + x2 + 4, L3 = x1 - 4x2 + 20, и система ограничений: x1 + x2 £ 15, 5x1 + x2 ³ 1, -x1 + x2 £ 5, x2 £ 20, "xj ³ 0. 2. Решение многокритериальной задачи линейного программирования графическим методом. 2.1.Формальное условие и сведение к ЗЛП Чтобы можно было ...
... конечные результаты при минимальных затратах ресурсов. Математический инструментарий, позволяющий решать экономические задачи оптимального типа, называется программированием. Различают линейное и нелинейное программирование. На практике наибольшее распространение получило линейное программирование. Методы линейного программирования в математике известны под названием общей задачи линейного ...
... 4 X1 + 2 X2 + 0 X3 + X4 = 19 0 X1 + 1 X2 + 1 X3 + X5 = 8 1 X1 + 2 X2 + 0 X3 + X6 = 24 Получили задачу: 4X1+2X2+X4 = 19 X2 + X3 +X5 = 8 X1+2X2 +X6 =24 3.3 Решаем задачу путем сведения к задаче линейного программирования: Xi≥0 ; 0-Z= -3X1- -7X2- -2X3 Приведем задачу к канонической форме. Задача ...
... условиях определенности математическое программирование дает точное решение поставленной задачи. Поэтому необходимости выбирать из нескольких вариантов попросту нет. Таким образом, в условиях определенности "Теория принятия решений" не используется, такими задачами занимается математическое программирование. 2) ЛПР знает вероятность реакции окружающей среды на выбор им той или иной альтернативы. ...
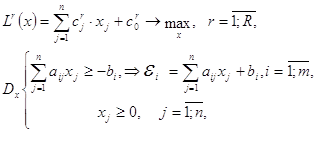
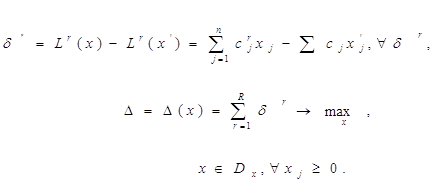


0 комментариев