Навигация
Оптимизационные методы решения экономических задач
23385
знаков
0
таблиц
0
изображений
Содержание
Введение
1 Оптимизационные методы решения экономических задач.
2 Многокритериальная оптимизация. Методы сведения многокритериальной задачи к однокритериальной
3 Гладкая оптимизация.
4 Выпуклая оптимизация. Условие выпуклости.
5 Экономико-математическая модель реструктуризации угольной промышленности. Критерий оптимизационной задачи
Заключение
Литература
Введение
Угольная промышленность является одной из базовых в народно-хозяйственном комплексе Украины. Уголь потребляется почти во всех отраслях народного хозяйства и определяет в основном темпы и возможный уровень развития производства черных и цветных металлов, электрической и тепловой энергии, других отраслей промышленности. Каменный и бурый уголь служат исходным сырьем для ряда отраслей химической промышленности.
Вследствие большой глубины угольных залежей и небольшой мощности пластов угольная промышленность Украины имеет худшие показатели добычи угля по сравнению с некоторыми странами СНГ и мира. Добыча угля в осуществляется в несоизмеримо худших горно-геологических условиях, чем в других странах мира. Это - главная объективная причина больших удельных затрат материальных, энергетических, трудовых ресурсов, а также того, что производительность труда намного ниже мировой. Кроме того, отрасль теряет наиболее подготовленных, квалифицированных специалистов. Большая часть шахт нерентабельна, т.е. суммарные затраты на добычу угля превышают его стоимость на рынке.
В настоящее время отрасль требует внедрения задач оптимизационного типа, в которых требуется найти наилучшее или оптимальное решение при заданных условиях производства. Опыт западноевропейских государств, практически завершивших оптимизационный процесс в угольной промышленности, и России, стартовые позиции которой сходны с Украиной, подтверждает необходимость поддержки и контроля со стороны государства при реализации намеченных программ.
Таким образом, необходимо отметить, что изучение экономических задач оптимизационного типа относящихся к угольной промышленности является актуальным предметом исследования. Наличие большого количества проблем требует детального их изучения и разработки направлений по их решению.
1 Оптимизационные методы решения экономических задач
К экономическим задачам оптимизационного типа относятся задачи, в которых требуется найти наилучшее или оптимальное решение при заданных условиях производства. Такие задачи называются задачами на максимум или минимум. Особенностью задач оптимизационного типа является многовариантность их решений, обусловленная следующими причинами: взаимозаменяемостью ресурсов; взаимозаменяемостью готовых видов продукции; существованием альтернативных технологий производства; неодинаковостью технико-экономических показателей даже однотипных хозяйственных субъектов.
Возможны два подхода к постановке оптимизационных задач: при первом подходе требуется получить максимальные конечные результаты при заданных условиях производства; при втором подходе требуется получить заданные конечные результаты при минимальных затратах ресурсов.
Математический инструментарий, позволяющий решать экономические задачи оптимального типа, называется программированием. Различают линейное и нелинейное программирование.
На практике наибольшее распространение получило линейное программирование.
Методы линейного программирования в математике известны под названием общей задачи линейного программирования. Аналитическая формулировка общей задачи линейного программирования. Общая задача линейного программирования формулируется следующим образом:
Найти решение {Х1,Х2,….Хn}, позволяющее максимизировать или минимизировать целевую функцию
F = C1X1+C2X2+…+ CnXn
при условиях
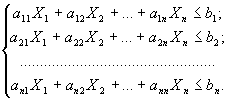
Х1≥0; Х2≥0; …; Хn≥0.
Это развернутая запись общей задачи линейного программирования. Сокращенная запись этой модели имеет вид:
Найти решение {Xj}, позволяющее максимизировать (минимизировать) функцию
при условиях
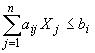, i = 1,2,…,n;
Xj ≥ 0, j = 1,2,…,n.
Вышеприведенные записи общей задачи линейного программирования называют аналитической формой записи.
Любое решение, удовлетворяющее условиям, называется допустимым решением. Допустимое решение систем неравенств, удовлетворяющее целевой функции, называется оптимальным решением. Такое решение единственно при заданных условиях.
Матричная форма записи общей задачи линейного программирования
при ограничениях AX≤B
X≥0
где С = (с1, с2,…, сn);
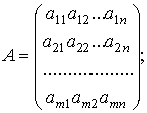
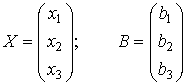
где С – матрица-строка
А – матрица системы
Х – матрица-столбец переменных
В – матрица-столбец свободных членов
Похожие работы
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
... во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные. 2. Области применения и ограничения использования линейного программирования для решения экономических задач Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление ...
... управления, прочие системы. Целью данной курсовой работы является рассмотрение, освещение и оценка возможностей пакета прикладных программ MS OFFICE с точки зрения информационных технологий и методов их использования при решении экономических задач. 2. Использование пакета прикладных программ MS OFFICE при решении экономических задач 2.1 Обзор возможностей Microsoft Office Пакет ...
... (нынешняя) стоимость или общая сумма, которая на настоящий равноценна серии будущих выплат; Тип - 0 или 1, Если 0 – оплата производится в конце периода, если 1, то в начале. В данной задаче функции приобретают вид ЧПС(0;D2;E2;F2) и БС(I2;B2;;-C2). 4. С помощью функции Подбор параметра определена ставка, при которой выгоднее деньги вложить в инвестиционный проект 8,5%. 1. Внесены исходные ...
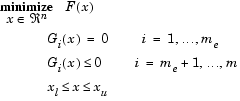
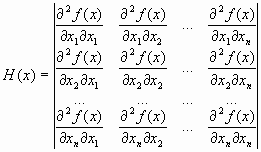
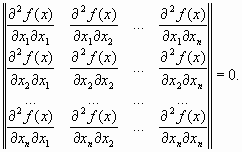
0 комментариев