Навигация
Исходные данные отложить на координатной плоскости и сделать предварительное заключение о наличии связи
4.1. Исходные данные отложить на координатной плоскости и сделать предварительное заключение о наличии связи.
таб.1 диагр.1
| x | y |
| 2,1 | 29,5 |
| 2,9 | 34,2 |
| 3,3 | 30,6 |
| 3,8 | 35,2 |
| 4,2 | 40,7 |
| 3,9 | 44,5 |
| 5,0 | 47,2 |
| 4,9 | 55,2 |
| 6,3 | 51,8 |
| 5,8 | 56,7 |
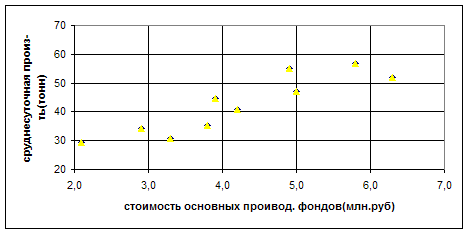
Вывод: Из диаграммы 1 видно, что связь между факторами x и y
прямая сильная линейная связь.
4.2.Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами х и у, используя шкалу Чеддока.
таб.2
| № |
|
|
|
| xy |
|
|
|
| 1 | 2,1 | 29,5 | 4,41 | 870,25 | 61,95 | 27,91 | 1,59 | 0,054 |
| 2 | 2,9 | 34,2 | 8,41 | 1169,64 | 99,18 | 33,46 | 0,74 | 0,022 |
| 3 | 3,3 | 30,6 | 10,89 | 936,36 | 100,98 | 36,23 | -5,63 | 0,184 |
| 4 | 3,8 | 35,2 | 14,44 | 1239,04 | 133,76 | 39,69 | -4,49 | 0,128 |
| 5 | 4,2 | 40,7 | 17,64 | 1656,49 | 170,94 | 42,47 | -1,77 | 0,043 |
| 6 | 3,9 | 44,5 | 15,21 | 1980,25 | 173,55 | 40,39 | 4,11 | 0,092 |
| 7 | 5,0 | 47,2 | 25 | 2227,84 | 236 | 48,01 | -0,81 | 0,017 |
| 8 | 4,9 | 55,2 | 24,01 | 3047,04 | 270,48 | 47,32 | 7,88 | 0,143 |
| 9 | 6,3 | 51,8 | 39,69 | 2683,24 | 326,34 | 57,02 | -5,22 | 0,101 |
| 10 | 5,8 | 56,7 | 33,64 | 3214,89 | 328,86 | 53,55 | 3,15 | 0,056 |
| ИТОГО: | 42,2 | 426 | 193,34 | 19025,04 | 1902,04 | 426 | 0,840 | |
| Среднее зн. | 4,22 | 42,56 | 19,334 | 1902,504 | 190,204 |
4.2.1.Проверим тесноту связи между факторами, рассчитаем ЛКК:
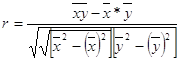 ;
;
Вывод: по шкале Чеддока связь сильная.
4.2.2.Проверим статистическую значимость ЛКК по критерию Стьюдента:
1)Критерий Стьюдента: tвыб<=tкр
2)Но: r=0 tкр=2,31
tвыб=rвыб*![]()
Вывод: таким образом поскольку tвыб=5,84<tкр=2,31, то с доверительной вероятностью
90% нулевая гипотеза отвергается, это указывает на наличие сильной линейной связи.
4.3.Полагая, что связь между факторами х и у может быть описана линейной функцией, используя процедуру метода наименьших квадратов, запишите систему нормальных уравнений относительно коэффициентов линейного уравнения регрессии. Любым способом рассчитайте эти коэффициенты.
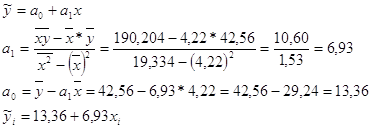
Последовательно подставляя в уравнение регрессии ![]() из графы (2) табл.2, рассчитаем значения и заполним графу (7) табл.2
из графы (2) табл.2, рассчитаем значения и заполним графу (7) табл.2
4.4.Для полученной модели связи между факторами Х и У рассчитайте среднюю ошибку аппроксимации. Сделайте предварительное заключение приемлемости полученной модели.
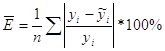
Для расчета заполним 8-ую и 9-ую графу табл.2
![]() <Екр=12%
<Екр=12%
Вывод: модель следует признать удовлетворительной.
4.5. Проверьте значимость коэффициента уравнения регрессии a1 на основе t-критерия Стьюдента.
![]()
![]()
![]()
![]() Решение: Таб.3
Решение: Таб.3
| № |
|
|
| |||
| 1 | 2,1 | 29,5 | 27,91 | 2,5281 | 214,623 | 170,5636 |
| 2 | 2,9 | 34,2 | 33,46 | 0,5476 | 82,81 | 69,8896 |
| 3 | 3,3 | 30,6 | 36,23 | 31,6969 | 40,069 | 143,0416 |
| 4 | 3,8 | 35,2 | 39,69 | 20,1601 | 8,237 | 54,1696 |
| 5 | 4,2 | 40,7 | 42,47 | 3,1329 | 0,008 | 3,4596 |
| 6 | 3,9 | 44,5 | 40,39 | 16,8921 | 4,709 | 3,7636 |
| 7 | 5 | 47,2 | 48,01 | 0,6561 | 29,703 | 21,5296 |
| 8 | 4,9 | 55,2 | 47,32 | 62,0944 | 22,658 | 159,7696 |
| 9 | 6,3 | 51,8 | 57,02 | 27,2484 | 209,092 | 85,3776 |
| 10 | 5,8 | 56,7 | 53,55 | 9,9225 | 120,78 | 199,9396 |
| ИТОГО: | 42,2 | 425,6 | 426,1 | 174,8791 | 732,687 | 911,504 |
| Среднее | 4,22 | 42,56 |
Статистическая проверка:
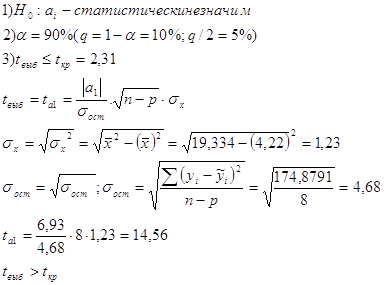
![]() Вывод: С доверительной вероятностью 90% коэффициент a1- статистически значим, т.е. нулевая гипотеза отвергается.
Вывод: С доверительной вероятностью 90% коэффициент a1- статистически значим, т.е. нулевая гипотеза отвергается.
0 комментариев