Навигация
Проверьте адекватность модели (уравнения регрессии) в целом на основе F-критерия Фишера-Снедекора
4.6. Проверьте адекватность модели (уравнения регрессии) в целом на основе F-критерия Фишера-Снедекора.
Решение:
Процедура статистической проверки:
![]() :модель не адекватна
:модель не адекватна
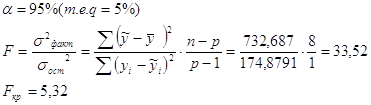
Вывод: т.к. Fвыб.>Fкр., то с доверительной вероятностью 95% нулевая гипотеза отвергается (т.е. принимается альтернативная). Изучаемая модель адекватна и может быть использована для прогнозирования и принятия управленческих решений.
4.7. Рассчитайте эмпирический коэффициент детерминации.
Решение:
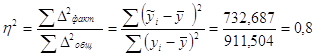 (таб. 3)
(таб. 3)
![]() -показывает долю вариации.
-показывает долю вариации.
Вывод: т.е. 80% вариации объясняется фактором включенным в модель, а 20% не включенными в модель факторами.
4.8. Рассчитайте корреляционное отношение. Сравните полученное значение с величиной линейного коэффициента корреляции.
Решение:
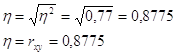
![]()
Эмпирическое корреляционное отношение указывает на тесноту связи между двумя факторами для любой связи, если связь линейная, то ![]() , т.е. коэффициент ЛКК совпадает с коэффициентом детерминации.
, т.е. коэффициент ЛКК совпадает с коэффициентом детерминации.
4.9. Выполните точечный прогноз для ![]() .
.
Решение:
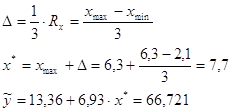
4.10-4.12 Рассчитайте доверительные интервалы для уравнения регрессии и для результирующего признака ![]() при доверительной вероятности
при доверительной вероятности ![]() =90%. Изобразите в одной системе координат:
=90%. Изобразите в одной системе координат:
а) исходные данные,
б) линию регрессии,
в) точечный прогноз,
г) 90% доверительные интервалы.
Сформулируйте общий вывод относительно полученной модели.
Решение:
![]() -математическое ожидание среднего.
-математическое ожидание среднего.
Для выполнения интервального прогноза рассматриваем две области.
1) для y из области изменения фактора x доверительные границы для линейного уравнения регрессии рассчитывается по формуле:
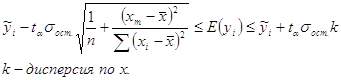
2) для прогнозного значения ![]() доверительный интервал для
доверительный интервал для ![]() рассчитывается по формуле:
рассчитывается по формуле:
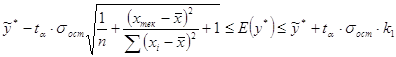
Исходные данные:
1) n=10
2) t=2,31(таб.)
3) ![]()
4)![]()
5)![]() : 27,91
42,56 57,02 66,72
: 27,91
42,56 57,02 66,72
6)![]() 19,334-4,222)=1,53.
19,334-4,222)=1,53.
Таб.4
| № |
|
|
|
|
|
|
|
|
|
|
|
| 1 | 2,1 | -2,12 | 4,49 | 3,03 | 1,74 | 2,31 | 4,68 | 18,81 | 27,91 | 9,10 | 46,72 |
| 2 | 4,22 | 0,00 | 0,00 | 0,1 | 0,32 | 2,31 | 4,68 | 3,46 | 42,56 | 39,10 | 46,02 |
| 3 | 6,3 | 2,08 | 4,33 | 2,93 | 1,71 | 2,31 | 4,68 | 18,49 | 57,02 | 38,53 | 75,51 |
| 4 | 7,7 | 3,48 | 12,11 | 9,02 | 3 | 2,31 | 4,68 | 32,43 | 66,72 | 34,29 | 99,15 |
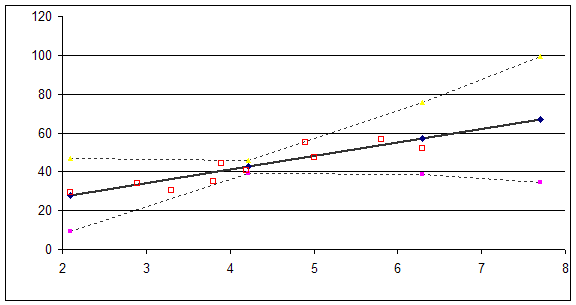
Вывод: поскольку 90% точек наблюдения попало в 90% доверительный интервал данная модель и ее доверительные границы могут использоваться для прогнозирования с 90% доверительной вероятностью.
0 комментариев