Ниже приведены данные о ситуации на рынке товара А
Тема: Теория потребительского выбора
Пусть эта функция в каждой точке, по крайней мере, дважды дифференцируема по каждому аргументу
Насколько потребитель увеличит закупки товара, который подешевел, т.е. эффект переключения спроса
На рис. показана одна из кривых безразличия потребителя и его бюджетная линия. Цена товара Y равна 12
Ресурсы абсолютно взаимодополняемые – изокванта 1
Признаком оптимального размера производства является равенство
Тема: Общее рыночное равновесие
Аукционист устанавливает любую начальную систему цен
В системе Вальраса очень слабо представлен финансовый сектор. Д.Потинкен достроил модель Вальрас моделями финансовых потоков
Потеря для потребителей;
Каждая фирма обладает относительно небольшой долей всего рынка, поэтому она имеет очень ограниченный контроль над рыночной ценой;
Навигация
На рис. показана одна из кривых безразличия потребителя и его бюджетная линия. Цена товара Y равна 12
Курс микроэкономики
214221
знак
34
таблицы
98
изображений
2.15. На рис. показана одна из кривых безразличия потребителя и его бюджетная линия. Цена товара Y равна 12.
а) Каков доход потребителя?
б) Какова цена товара Х?
в) Как изменится положение бюджетной линии при увеличении цены товара Y до 15? При снижении до 10?
г) Напишите уравнение бюджетной линии для каждого варианта.
2.16. Допустим, потребитель имеет месячный доход М=200. на рис. показаны две бюджетные линии и соответствующие им кривые безразличия.
а) Какова цена товара Y?
б) Определите координаты двух точек линии спроса данного потребителя на товар Х?
в) Зависит ли положение данной линии спроса от цены товара Y, от дохода потребителя?
2.17. Потребитель приобретает товары X и Y. Товар Y продается по цене 2 дол. за единицу. Товар X продается по цен 10 дол. за единицу, если объем покупки не превышает 20 единиц, а за каждую следующую (сверх 20) покупатель платит 5 дол. Пусть доход М=300. Покажите графически бюджетное ограничение при этих условиях. Товары X и Y – нормальные. Укажите наиболее предпочтительный набор.
2.18.Предположим, потребитель выбирает между двумя товарами X и Y. При заданных начальных ценах товаров и доходах потребитель, максимизирующий полезность, делает следующий выбор: X=4, Y=5 ед. Допустим, цены товаров и доходов изменились таким образом, что бюджетная линия описывается уравнением: Y=14–0,75Х. Увеличилась ли для потребителя максимально достижимая полезность? Объясните ответ графически.
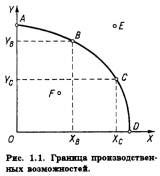
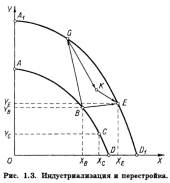
2.19. Проанализируйте график на рис. и ответьте на вопросы:
а) Если доход потребителя равен 300, какова цена товаров X, Y?
б) Чему равна норма замещения в точке А?
в) Может ли предельная норма замещения в точке В равняться 5?
г) Если доход потребителя не меняется, как бы должны измениться цены товаров X, Y, чтобы точка В стала точкой равновесия потребителя?
2.20.Функция спроса на вино Q=0,02M–2P, где М – доход, Р – цена бутылки вина, Q – количество бутылок вина. Пусть М=7500, Р=30.
а) Если цена вина вырастет до 40, то каким должен стать доход, чтобы спрос на вино оставался прежним? При этом доходе и новой цене сколько бутылок вина будет куплено?
б) Чему равен эффект замещения и эффект дохода при повышении цены на вино до 40?
2.21. Рассмотрите рис. и ответьте на вопросы:
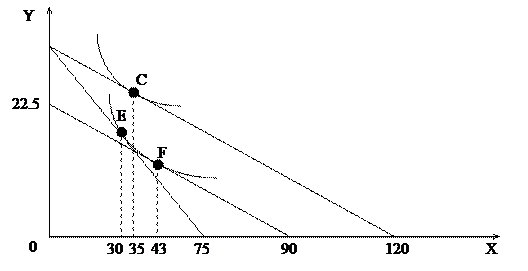
а) Если доход М=300, Рх=4, Ру=10, сколько товара Х потребляется при этих условиях?
б) Если цена товара Х упадет до 2,5 (при прочих неизменных условиях), каков будет спрос на товар Х?
в) Найдите эффект замены и эффект дохода в общем изменении спроса на товар Х.
г) Каким товаром – нормальным или низшим – является благо Х?
д) Нарисуйте на отдельном графике кривую Энгеля и кривую спроса для товара Х.
3. Тема: Теория производства и конкурентной фирмы
Глава 1: Абстрактная теория производства.
№1. ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ.
Пожалуй, самой простой формой представления производства является модель «чёрного ящика».
;
F – это земля, капитал, труд, предпринимательская способность. Но иногда удобнее рассматривать только один фактор, т.е. остальные не имеют значения. Функция может быть:
· однофакторная и однопродуктовая;
· однопродуктовая и многофакторная;
· многопродуктовая и многофакторная;
Производственная функция, если задана, описывает некоторую технологию. Если задана технология, значит, есть производственная функция. Если технология задана и если мы знаем затраты F, мы можем легко вычислить выпуск Q.
Конечно, существуют различные технологии, однако далее мы рассматриваем только эффективные технологии. Эффективная технология – наиболее производительная из существующих. Заданный объем выпуска – меньше ресурсов; задан объем ресурсов – больше выпуска.
Из всевозможных производственных функций основное внимание уделяется функциям с неоклассическими свойствами:
1. 
;
2. Функция должна быть дважды дифференцируема;
3. 
– предельный продукт фактора (MPF);
4. 
– убывающая отдача дополнительных затрат фактора.
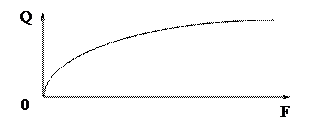
№2. ОДНОФАКТОРНАЯ ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ.
Рассмотрим однофакторную производственную функцию при условии нехватки труда. Остальные условия мы берем неизменными. Исследуем, как будет увеличиваться выпуск продукции в зависимости от труда.
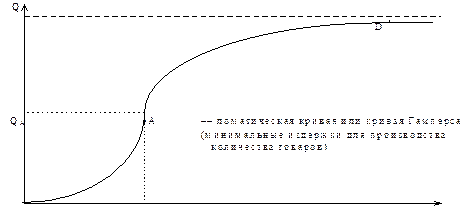
На графике
А – точка перегиба.
Затраты от 0 до FA дают по сравнению с предыдущей большую отдачу. Вторая производная больше 0. После FA – постоянно уменьшающаяся отдача. В точке D полное насыщение производства. Это график стандартной технологии.
Условие задачи:
Пусть:
– средний продукт (средняя производительность фактора)
– показатель предельной производительности.
МР показывает, насколько увеличится производство при затрате последней единицы фактора.
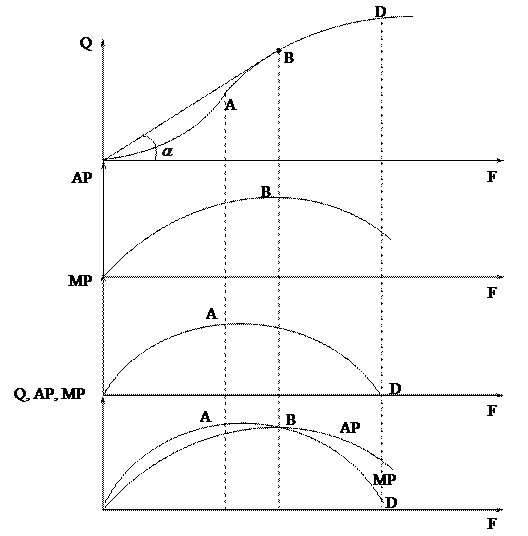Пояснения к рисунку.
Каждая единица фактора имеет разную отдачу. Показатель AP характеризует отдачу от всех затрат, но очень важно знать тенденцию, т.е. как будет изменяться выпуск в зависимости от каждой следующей единицы затрат фактора. Об этом нам говорит MP.
Рассмотрим характеристики стандартной технологии с точки зрения последовательных затрат фактора. На интервале (1) каждая последовательная единица фактора дает нам все большую отдачу, следовательно, предельная производительность растет, а с ней растет и AP, вплоть до точки А
На участке (2) каждая последующая единица дает все меньшую отдачу, но, тем не менее, отдача каждой следующей единицы все еще выше, чем средняя отдача всех предшествующих затрат, следовательно, АР растет, вплоть до точки В.
Отдача от дополнительной единицы факторов в точке В равна отдаче от всех предшествующих затрат, следовательно, АР = МР.
На участке (3) каждая дополнительная единица фактора дает меньше отдачи, чем в среднем все предшествующие, поэтому понижение МР ведет к снижению АР до точки D. После точки D новые затраты фактора дают нулевой эффект.
Свойства графика:
· Максимальная отдача – в точке А.
· Максимальная средняя отдача – в точке В.
· Максимальный выпуск продукции – в точке D.
– если затраты фактора увеличить в n раз.
Мы анализируем «эффект масштаба производства». Нам надо сравнить n и m.
Если затраты F увеличить в n раз, а производство увеличится меньше, чем в n раз (m<n), то имеем потери от масштаба. Если m>n, то имеем экономию от масштаба – положительный эффект масштаба производства. Оптимальные размеры производства с точки зрения технологии связаны с эффектом масштаба. Для стандартной технологии положительный эффект масштаба производства, оптимальный режим, дальнейшее расширение – потери от масштаба.
№3. ОДНОПРОДУКТОВАЯ ДВУХФАКТОРНАЯ МОДЕЛЬ.
Нам необходимо рассмотреть эффекты взаимзаменяемости и взаимодополняемости факторов. Благодаря выводам, полученным при изучении двухфакторной модели, результаты этого изучения мы можем использовать для распространения на многофакторные модели.
Мы имеем дело с неоклассической функцией:
· 
;
· 
;
· 
;
Возможности взаимной замены факторов несколько ограничены.
F (K0, L0) Þ Q0 – выпуск продукции в точке А. Q0 = const. Требуется найти все комбинации F при которых объем выпуска будет постоянен и равен Q0.
Изокванта производственной функции – это геометрическое место всех комбинаций ресурсов, при которых выпуск продукции остается постоянным.
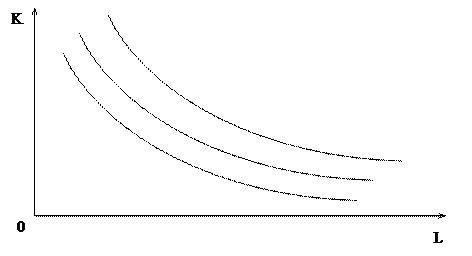
Для данной технологии требуется рассмотреть все возможные значения выпуска в зависимости от затрат ресурсов.
Получаем семейство изоквант для данной технологии. В идеале мы должны считать, что изокванты непрерывны. Для одной и той же технологии изокванты не пересекаются. Для неоклассической производственной функции изокванты не пересекают оси координат. Чем больше выпуск Q, тем изокванта дальше от начала координат. Если мы движемся по изокванте, мы можем рассмотреть возможности взаимной замены ресурсов при постоянном выпуске Q в условиях данной технологии.
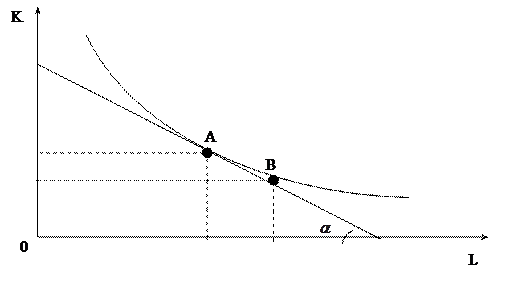
– интервальная норма замещения.
– очень маленькое приращение в окрестностях одной точки.
Предельная норма технического замещение (MRTS) показывает возможности замещения ресурсов в каждой точке.
Показатель MRTS должен быть связан с МР:
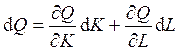
Виды изоквант:
Похожие работы
... , порнографией и т.п. Однако деятельность подобных субъектов также не привлекает особого внимания микроэкономики.[5,c.28] В целом микроэкономика имеет дело с субъектами экономики как производителями и потребителями и, соответственно, как покупателями и продавцами, объясняя их поведение в системе экономических отношений по поводу производства, обмена, распределения и потребления товарных благ. Эти ...
... подхода. [9, с. 35] На основе рассмотренных особенностей можно заключить, что предметом изучения микроэкономики является поиск и выбор рациональных экономических решений и действий отдельными субъектами экономики в процессе их хозяйствования. 2. Методология и методы микроэкономики 2.1 Общенаучные методы познания современной микроэкономики Методология экономической теории – это наука ...
... функциональный анализ и равновесный подход. 16. Методы статики и динамики, предельный анализ. 17. Дайте характеристику экономических моделей и экономических переменных. 18. Какова связь микроэкономики со вторыми экономическими и социальными науками? 19. Что представляет собой индивидуальный экономический субъект? 20. Какой смысл имеет позитивный и нормативный анализ в ...
... предприниматель рискует всем своим имуществом, в отличие от акционеров, которые рискуют только активами фирмы, а не своим имуществом.[13,c.57] 2. Роль предпринимательства в микроэкономике 2.1 Роль предпринимательства в экономике Развитие предпринимательства является одним из самых точных показателей экономического и социального уровня государства. Предпринимательство обеспечивает: 1. ...
0 комментариев