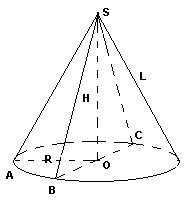
Понятие конуса: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Коническая поверхность называется боковой поверхностью конуса, а круг – основанием конуса
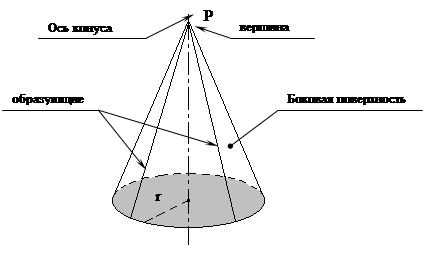
Получение конуса: конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.
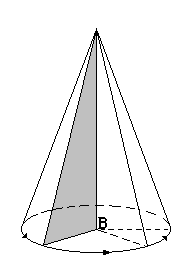
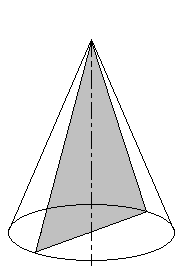
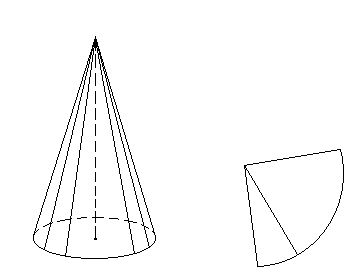
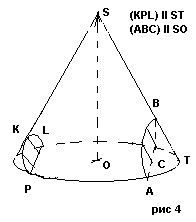
Сечение конуса: если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым.
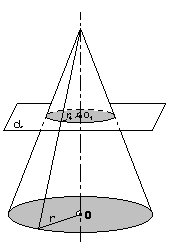
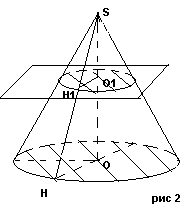
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О1, расположенной на оси конуса.
Площадь поверхности конуса: разверткой боковой поверхности конуса является круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора – длине окружности основания конуса. За площадь боковой поверхности конуса принимается площадь ее развертки.
где α – градусная мера дуги АВА1

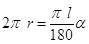
откуда 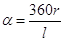

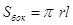
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
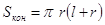
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.
Усеченный конус, его получение и площадь:







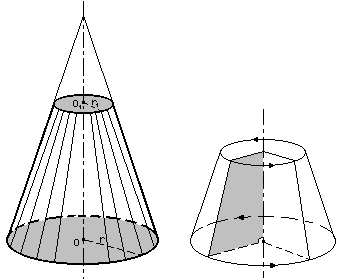
Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.
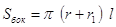
Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую.
Раздел:
Математика Количество знаков с пробелами: 1591
Количество таблиц: 0
Количество изображений: 6
... Е+ называются н-дизъюнктными или ортогональными по Роберу (обозначается x у), если ||x + λу|| = ||x – λу|| для любого λ ≥ 0. 2. Описание множеств |Х|, Х+, Х- Рассмотрим пространство , упорядоченное регулярным круглым конусом K(f,a), где a = 0,5 и функционал f имеет первую координату, равную единице, а остальные координаты нулевые: K1 = {x = (x1, x2, ..., xn) : x1 ≥ |x2| ...
... АВ= L образующая ,α угол наклона образующе и плоскости нижнего основания. Отрезок О1О2-высота. Трапеция АВСD – осевое сечение. Н=L*sin α H²+(R-r) ²=L² Около усеченного конуса всегда можно описать шар. Его центр лежит на прямой О1О2 CF=FD OF┴Cd=> О – центр описанного шара R - радиус описанного шара, равный радиусу окружносит описанной ...
... . Найдите площадь осевого сечения, площадь полной поверхности конуса и его объем. II. Примените полученные знания на практике. Комментарии учителя: Итак, Вы уже знаете как найти элементы конуса, его поверхность и объем, но сможете ли Вы применить их выходя на “вольный воздух”. Ведь куча щебня по краям шоссейной дороги также представляет предмет заслуживающий внимания. Посмотрев на рисунок 1, мы ...
...
c=36.49-R2
.Линия
пересечения
симметрична
относительно
луча j=0;
ветвь, соответствующая
знаку «-»
в формуле
(IX),
посторонняя. Описание линии пересечения конусов на выкройке первого конусаПодставляя
параметризацию
первого конуса
(IX),
в уравнение
второго конуса(V),
получаем
уравнение:
(rsinbcos+7.7)2tg2b=(-7.7+rcosb)2+r2sin2bsin2 квадратное
уравнение
относительно
переменной
r.После
упрощения
...





![]()
![]()
![]()
![]()
![]()
![]()

![]()
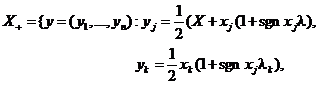
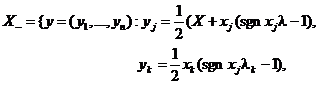


0 комментариев