Курсовая работа по информатике
Вполнил студент Дюмеев Данил
Южно-Уральский Государственный Университет
Аэрокосмический факультет
Кафедра летательных аппаратов
При а =0.1
![]()
Интервал изменения параметра x
![]()
![]()
Строим график функции
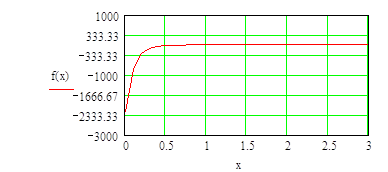
При интервале изменения коэффициента x
![]()
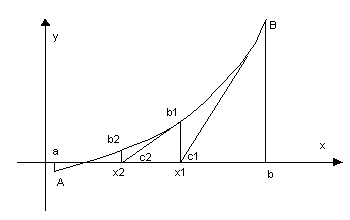
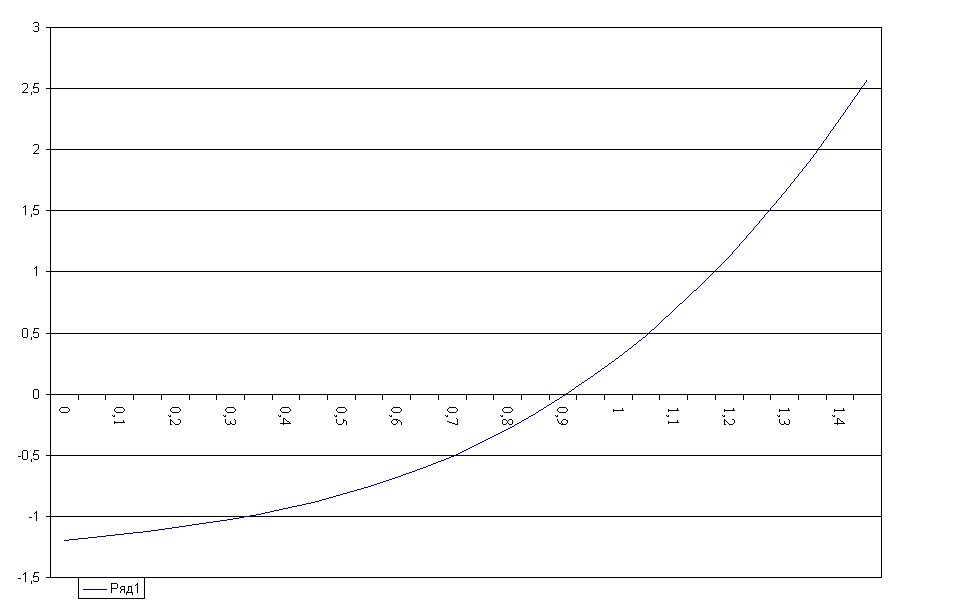
График имеет вид
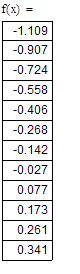
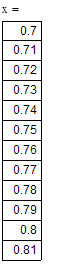
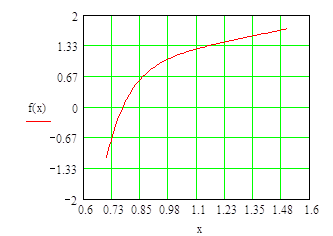
При а=0 функция f(x)=0 имеет значения корня x=0.77
Находим более точное значение корня
![]()
![]()
-вычислительный блок
![]()
![]()
-процедура нахождения корня
![]()
-более точное значение корня
Проверка:
![]()
При а =1
![]()
Интервал изменения параметра x
![]()
![]()
Строим график функции
При интервале изменения коэффициента x
![]()
График имеет вид
При а=1 функция f(x)=0 имеет приближенное значения корня x=0,21
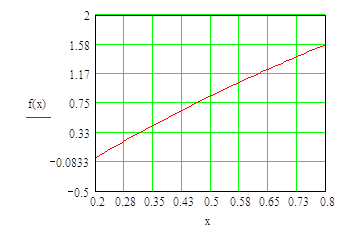

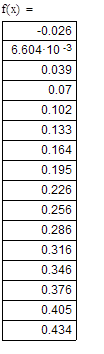
Находим более точное значение корня
![]()
![]()
-вычислительный блок
![]()
![]()
-процедура нахождения корня
![]()
-более точное значение корня
Проверка:
![]()
При а =2
![]()
Интервал изменения параметра x
![]()
![]()
Строим график функции
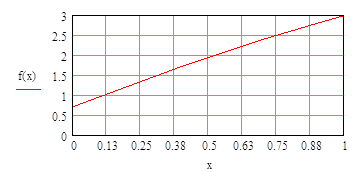 При интервале изменения коэффициента x
При интервале изменения коэффициента x
![]()
График имеет вид
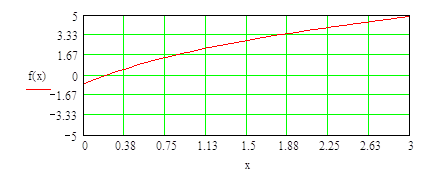
При а=2 функция f(x)=0 имеет приближенное значения корня x=-0,25
Находим более точное значение корня
![]()
-вычислительный блок
![]()
![]()
-процедура нахождения корня
![]()
-более точное значение корня
Проверка:
![]()
Нахождение более точного значения корня при помощи root
![]()
![]()
![]()
-приближенное значение корня
![]()
![]()


Находим min и max функции
![]()
![]()
![]()
-шаг изменения аргумента
![]()
![]()
- на интервале от -10 до 10
![]()
- на интервале от -10 до 10
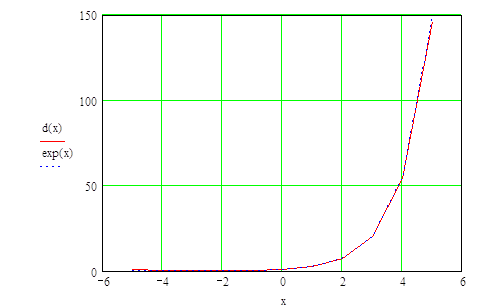
Разложение функции d(x)=exp(x) в степенной ряд
![]()
- интервал изменения аргумента
![]()
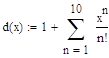
![]()
Похожие работы
... –0.6 = 0 9. 10. ( x -1)3 + 0.5ex = 0 11. 12. x5 –3x2 + 1 = 0 13. x3 –4x2 –10x –10 = 0 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. x 4- 2.9x3 +0.1x2 + 5.8x - 4.2=0 25. x4+2.83x3- 4.5x2-64x-20=0 26. МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 1. Постановка задачи Пусть требуется решить систему n ...
... искомого интервала [a, b] являются переменными величинами, которые должны задаваться в каждом конкретном случае с учетом физического смысла решаемой задачи. На втором этапе решения нелинейных уравнений полученные приближенные значения корней уточняются различными итерационными методами до некоторой заданной погрешности. Наиболее эффективные методы уточнения корней уравнения рассмотрены ниже. ...
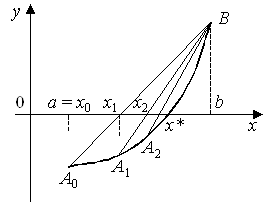
... : в работе инженера. СОДЕРЖАНИЕ стр. ВВЕДЕНИЕ........................................ 5 1. Краткое описание сущности метода касательных ( метода секущих Ньютона).................... 7 2. Решение нелинейного уравнения аналитически .. 9 3. Блок схема программы ........................ 11 4. Программа на языке ...
... (можно предположить единственность корня) Корень отделен на интервале Границы исходного отрезка сдвигаются () Воспользуемся приведенным выше алгоритмом для отделения корня уравнения на заданном отрезке: 1. Разобьем интервал изоляции корня на n отрезков равной длины: 2. Вычисляем значения функции в точках : 3. На концах отрезка (1;2) функция имеет разные ...
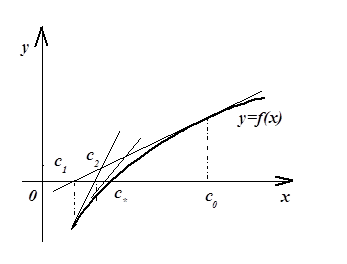
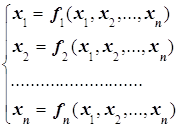
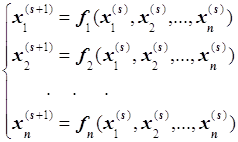
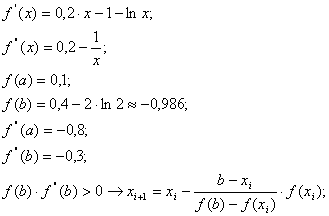
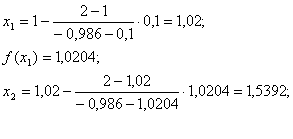

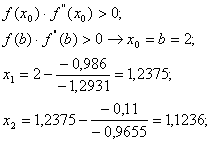
0 комментариев