Усиление контрастности
Состав технических средств АРМ ВР
Цифровая рентгенография с экрана электронно-оптического преобразователя (ЭОП)
Математическая постановка задачи рентгеновской компьютерной томографии, преобразование Радона и формулы обращения
Приведение формул обращения томографической реконструкции в конусе лучей к виду, позволяющему строить численные алгоритмы
Элементы теории обобщенных функций в применении к задачам обращения лучевого преобразования
Соотношения между преобразованиями Радона, Фурье и лучевым преобразованием
Навигация
Математическая постановка задачи рентгеновской компьютерной томографии, преобразование Радона и формулы обращения
Средства визуализации изображений в компьютерной томографии и цифровых рентгенографических системах
83583
знака
1
таблица
12
изображений
4.1. Математическая постановка задачи рентгеновской компьютерной томографии, преобразование Радона и формулы обращения.
В компьютерной рентгеновской томографии трехмерный объект представляется обычно в виде набора тонких срезов. Для восстановления плотности среза решается задача обращения двумерного преобразования Радона. Преобразованием Радона функции f(x, y) называется функция, 
определяемая равенством 
.
Обычно для восстановления функции двух переменных по ее интегралам вдоль прямых используется метод свертки и обратного проецирования. В этом методе формула обращения преобразования Радона записывается без явного использования обобщенных функций. Однако наиболее общий и естественный вид формулы обращения преобразования Радона приобретают при использовании аппарата обобщенных функций. Далее будет рассмотрено соотношение между методом обобщенных функций и методом свертки и обратного проецирования.
Перед изложением собственно численного алгоритма будет дан вывод формулы обращения, позволяющий естественным образом перейти к построению алгоритма.
В силу равенства
функция 
при любом фиксированном p определяется своими значениями при 
. Это позволяет нам перейти к функции
.
Здесь L(r, φ) - прямая, ортогональная лучу, имеющему угол φ ρ положительным направлением оси X, и отстоящая от начала координат на расстояние r (r
0), при r < 0 L(r, φ) - прямая, симметричная относительно начала координат прямой L(|r|, φ). Выразим f(x, y) через I(r, φ).
Поскольку
,
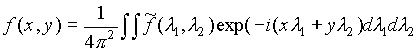где 
- преобразование Фурье функции f, то, переходя к полярным координатам после элементарных преобразований интеграла по φ на интервале [π, 2π], οолучаем
.
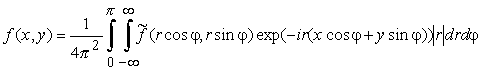Введем функцию S(z, φ), полагая
.
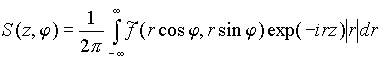При фиксированном φ функция S(z, φ) εсть обратное одномерное преобразование Фурье от произведения 
и |r|. Для справедливо равенство
.
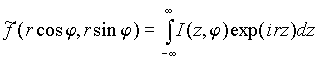Обратное преобразование Фурье от |r| есть обобщенная функция v1/πz2. Переходя от преобразования Фурье произведения к свертке, получаем S(z,φ) = I(z,φ)
(v1/πz2). Используя регуляризацию функции 1/z2 [19] приходим к выражению
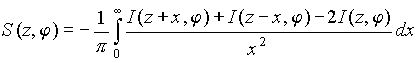. (1.5.1)
Таким образом, для f(x, y) справедлива формула
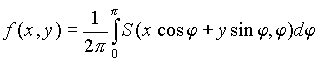, (1.5.2)
позволяющая выразить искомую функцию через наблюдаемые данные.
Прежде чем перейти к дискретному варианту сделаем ряд замечаний, связанных с обоснованием корректности рассматриваемых алгоритмов в реальных ситуациях. Обобщенные функции являются функционалами над пространством бесконечно дифференцируемых быстро убывающих функций. Однако при построении аппроксимаций исходных реальных данных по отсчетам, заданным в дискретных точках, желательно иметь менее жесткие требования к гладкости аппроксимирующих функций. Свертка с обобщенными функциями, в частности, с функцией 1/z2, может быть определена для значительно менее гладких функций, это очень важно при доказательстве корректности применения численных алгоритмов, получаемых с помощью аппарата обобщенных функций, к реальным данным.
Перейдем к дискретному варианту. Будем предполагать, что f(x, y) = 0 вне круга радиуса R с центром в нуле. Исходными данными являются величины I(ri, φi), здесь ri v отсчеты в интервале [-R, R], 1 ≤ i ≤ M - отсчеты в интервал [0, π], 1 ≤ j ≤ N. Если теперь при заданных значениях функции I(r, φ) β отсчетах (ri, φi) построить аппроксимацию I(r, φ) так, что для S(z,φ) βыполняется равенство (1.5.1), то используя (1.5.1) и (1.5.2) можно получить приближение к f(x, y). В дальнейшем будем предполагать, что отсчеты на осях r и φ являются равноотстоящими.
При каждом фиксированном φj определим 
следующим образом.
1. Функция имеет непрерывную первую производную по r.
2. В узлах решетки аппроксимирующая функция совпадает с заданными отсчетами, а ее производная в этих точках равна выборочной. То есть справедливы равенства: 
, 
, здесь h = 2R/(M-1), I(r0,φj) = I(rM+1, φj) = 0, i = 1, -, M.
3. На интервале [ri, ri+1] функция есть полином третьей степени от r.
Перечисленные условия позволяют в явном виде получить коэффициенты соответствующего сплайна. Непосредственными вычислениями можно получить, что
,
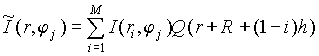где
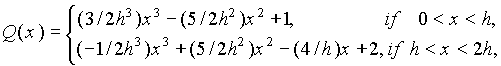
Q(x) = Q(-x), Q(x) = 0 при |x|> 2h, h=ri+1-ri.
Функция Q(x) имеет разрывы второй производной, но модуль второй производной интегрируем, используя это обстоятельство можно показать, что свертка S0(z) = Q(x) (-1/πz2) выражается формулой (1.5.1). Непосредственными вычислениями получаем
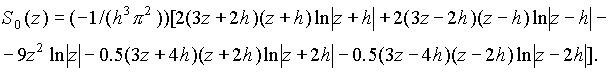
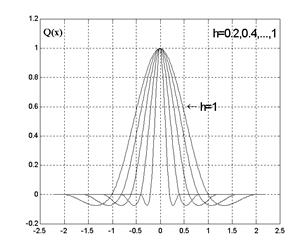
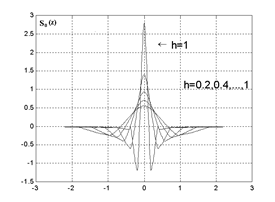
Графики функций Q(x) и S0(z) для различных значений h представлены на рис. 1 и рис. 2.
Таким образом,
.
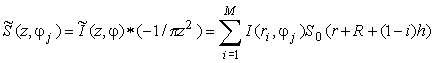Заменяя в (1.5.2) S на 
и интеграл частной суммой, получаем f*(x, y) - приближение к функции f(x, y),
. (1.5.3)
Как уже отмечалось выше, обычно в компьютерной томографии используется метод свертки и обратного проецирования. Рассмотрим соотношение между этим методом и методом, изложенным в настоящем параграфе. Используя интегрирование по частям, свертку с обобщенной функцией 1/z2 можно заменить дифференцированием и сверткой с 1/z (преобразованием Гильберта).
То есть функцию
S(z, φ) = I(z, φ) 1/z2
можно представить в виде
S(z, φ) = Iz/(z, φ) 1/z
При построении численных алгоритмов вместо обобщенной функции 1/z или, что то же самое, интеграла в смысле главного значения, в методе свертки и обратного проецирования используют некоторую последовательность регулярных функций pА(z), сходящуюся к 1/z (в смысле обобщенных функций) при A стремящемся к бесконечности. Используя интегрирование по частям, дифференцирование переносят на функции pА(z) и таким образом получают регулярные функции, сходящиеся к 1/z2, то есть свертка с обобщенной функцией 1/z2 заменяется последовательностью сверток с регулярными функциями p/А(z).
Таким образом, шаг свертки в классическом методе можно интерпретировать следующим образом: исходные данные аппроксимируются ступенчатой функцией и осуществляется свертка с регулярной функцией, являющейся приближением к обобщенной функцией 1/z2.
В методе настоящего параграфа исходные данные аппроксимируются более гладкими функциями - сплайнами 3-го порядка. Это позволяет точно вычислить свертку с обобщенной функцией 1/z2, причем в явном виде.
Шаг обратного проецирования соответствующий интегрированию свертки в обоих алгоритмах одинаков.
При использовании алгоритмов в реальных ситуациях важно уметь оценивать влияние шумов на точность получаемых приближений. Наличие явного выражения для аппроксимирующей функции позволяет вычислить дисперсию ошибки в любой точке при фиксированных δr, δφ θ известных статистических характеристиках шума. Для случая независимого, аддитивного, стационарного шума ξ (z) можно сделать следующее замечание. Рассмотрим процесс η, являющийся сверткой с 1/z2 процесса ξ. Спектральная плотность этого линейного преобразования есть |λ|. Для спектральных плотностей процессов ξ и η получаем соотношение f η (λ) = |λ|2fξ (λ). Δисперсия процесса η конечна, если интегрируема fη (λ), ςо есть процесс ξ дифференцируем в среднеквадратическом. Для того, чтобы свертка выражалась формулой (1.5.1), на процесс ξ нужно наложить дополнительные условия, потребовав, например, чтобы выборочные функции с вероятностью единица имели конечную вторую производную.
Численное моделирование и восстановление плотности реальных объектов с использование метода, изложенного в настоящем параграфе, показало высокую точность метода, особенно при исследовании объектов и дефектов, имеющих сложную конфигурацию и участки с резкими границами.
Примеры восстановления, с использованием методов, изложенных в настоящем параграфе, приведены на рисунке 3. Тестовый объект состоит из 10 частиц. Рис.3(слева) соответствует 10 поворотам и Рис.3 (справа) соответствует 32 поворотам.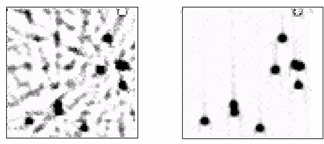 
Похожие работы
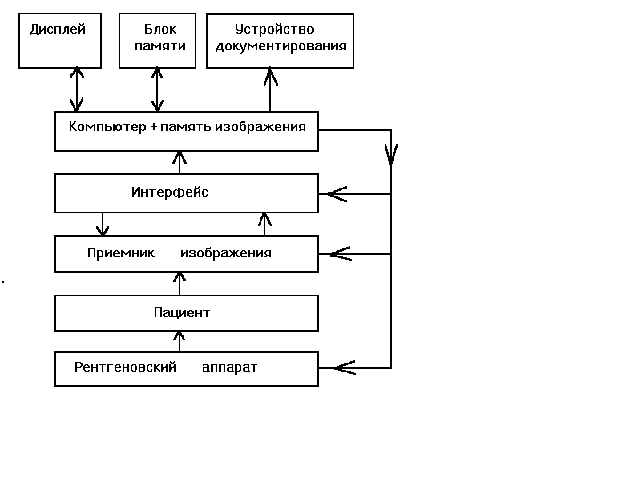
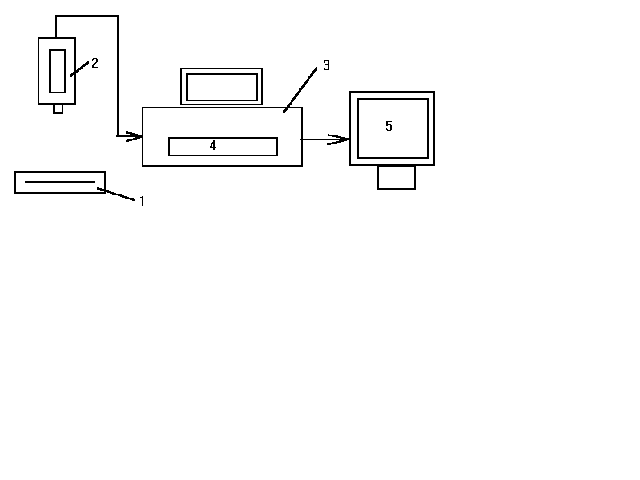
... более дорогостоящими, нежели обычные рентгеновские системы, однако по мере развития компьютерной техники и систем визуализации находят все более широкое применение. Цифровая рентгенодиагностика обеспечивается компьютерной технологией.Дисплей Блок долговременной памяти Устройство документирования Компьютер + память изображенияИнтерфейс данныхПриемник изображения Пациент Рентгеновский аппарат ...
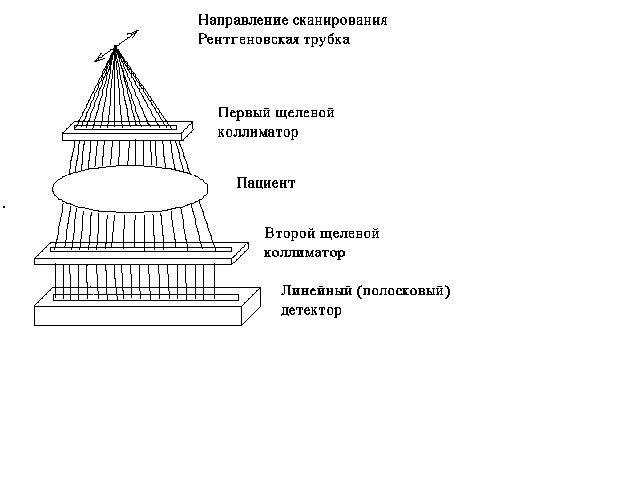
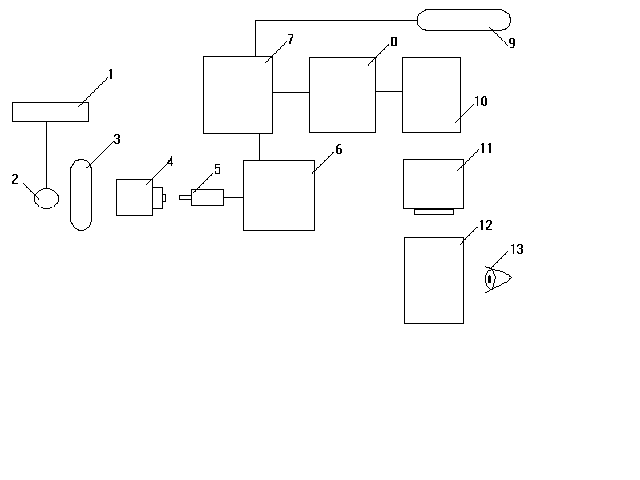
... обычная система электронно-оптического преобразования для просвечивания, из ЭОП, телевизионного тракта с высоким разрешением, рентгеновского высоковольтного генератора и рентгеновского излучателя Рис.5 Цифровая рентгенография с экрана ЭОП 1-генератор; 2-рентгеновская трубка; 3-пациент; 4-ЭОП; 5-видеокамера; 6-аналого-цифровой преобразователь; 7-накопитель изображений; 8-видеопроцессор; 9-сеть; ...
... банковских систем. Наиболее популярны сегодня смешанные решения, при которых часть модулей банковской системы разрабатывается компьютерным отделом банка, а часть покупается у независимых производителей. Основными платформами для банковских систем в настоящее время считаются: 1. ЛВС на базе сервера PC (10,7%); 2. Различные модели специализированных бизнес-компьютеров фирмы IBM типа AS/400 ...
0 комментариев