Элементы теории обобщенных функций в применении к задачам обращения лучевого преобразования

4.3 Элементы теории обобщенных функций в применении к задачам обращения лучевого преобразования

Обобщенная функция это непрерывный линейный функционал на пространстве К всех функций a (x), имеющих производные всех порядков и финитный носитель (свой для каждой из функций α (x)). Любая регулярная интегрируемая функция f(x) задает линейный функционал (f, a ):

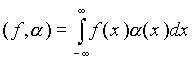. (2.2.1)

Однако на пространстве функций K существуют непрерывные линейные функционалы, которые не могут быть заданы с помощью регулярных интегрируемых функций, наиболее известными примерами таких функционалов являются δ-функция и ее производные. Другим широко известным примером является функционал, основанный на функции (1/x)dx. Функция 1/x x является регулярной, однако она не является интегрируемой. При задании соответствующего функционала интеграл

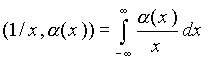(2.2.2)

понимается в смысле главного значения:

.

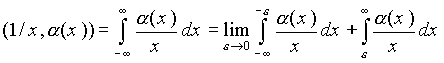Такое понимание интеграла используется при определении преобразования Гильберта от функции α (x) как свертки с функцией 1/xx.

.

Преобразование Гильберта используется, в частности, в одной из формул обращения преобразования Радона в двумерном пространстве. Эта формула обычно приводится в руководствах по компьютерной рентгеновской томографии. Однако метод свертки и обратного проецирования, часто используемый при построении численных алгоритмов томографической реконструкции, основан на несколько другом виде формулы обращения преобразования Радона. В этом методе по существу используется свертка проекционных данных последовательностью функций сходящихся к 1/xx² в смысле обобщенных функций.

Линейный функционал, соответствующий функции 1/xx², или, что то же самое, обобщенная функция 1/xx² определяется формулой [19]

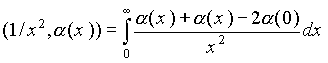(2.2.3)

Интеграл в (2.2.3) сходится в обычном смысле для любой функции a (x) из пространства основных, и даже из более широкого класса, функций.

В формулах обращения преобразования Радона используется свертка данных с функцией 1/xx². Свертка обобщенных функций определяется следующим образом.

Пусть заданы два функционала f и g . Действие функционала f *g являющегося их сверткой, на функцию a из пространства основных задается формулой

(f *g, a )= (f_x, g_y, a (x + y))). (2.2.4)

Здесь g_y означает, что функционал действует на функцию a , как функцию переменной y, а функционал f действует на полученную функцию переменной x. Если функционалы f и g можно задать регулярными функциям, то функционал свертки определенный формулой (2.2.4) можно задать функцией, являющейся сверткой соответствующих функций в обычном смысле.

Здесь следует сделать одно замечание. Даже если функция одной переменной a (t ) имеет финитный носитель, функция двух переменных a (x + y) не является функцией с финитным носителем. Это означает, что существование функционала f *g для конкретных функционалов f и g или необходимо доказывать. Известно, что для существования функционала свертки, достаточно, чтобы один из функционалов имел финитный носитель.

Если рассматривать задачи томографии, то там с функцией 1/xx² сворачиваются исходные данные, которые регулярны и имеют финитный носитель. Можно показать также, что необходимая свертка выражается формулой:

S(r, j ) = I(r, j ) * (-1/p r² ) =

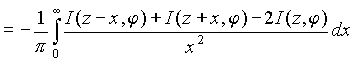(2.2.5)

В реальных ситуациях функция I(r, j ) известна в некотором дискретном множестве точек. Для того, чтобы использовать формулу (2.2.4) нужно построить аппроксимацию функции I(r, j ), такую что интеграл в правой части имеет смысл. Интеграл (2.2.4) заведомо сходится, если функция I(r, j ) принадлежит множеству K, то есть имеет финитный носитель и является бесконечно дифференцируемой.

Однако аппроксимация данных бесконечно дифференцируемой функцией может оказаться громоздкой при построении численных алгоритмов. Кроме того, использование бесконечно дифференцируемых функций может приводить к заглаживанию границ областей с резко отличающимися плотностями. Для сходимости интеграла в (2.2.5) достаточно, чтобы функция I(r, j ) имела в каждой точке конечные односторонние производные первого порядка по переменной r. Это позволяет, в частности, использовать кубические сплайны для построения аппроксимации функции I(r, j ).

Основными операциями с обобщенными функциями, используемыми в задачах томографии, являются свертка, дифференцирование и преобразование Фурье. Основная идея определения операций заключается в том, что некоторые свойства функционалов, задаваемых регулярными функциями, берутся за основу при определении соответствующих операций над обобщенными функциями, являющимися линейными функционалами.

На этой основе построено приведенное выше определение свертки. Особенно просто и наглядно этот прием можно продемонстрировать при определении операции дифференцирования обобщенных функций.

Пусть линейный функционал f задается регулярной функцией f(x) имеющей интегрируемую производную. Для действия производной на функцию a (x) из пространства основных можно записать равенство

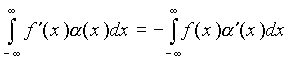, (2.2.6)

здесь использовано интегрирование по частям и то, что a (x) равна нулю вне некоторого конечного интервала.

Приведенное выше свойство берется за основу при определении производной обобщенной функции. Пусть задан функционал f, его производной называется функционал f^/, определяемый равенством . Так как функции из пространства основных бесконечно дифференцируемы, то определение является корректным и обобщенные функции имеют производные любого порядка.

Перейдем к определению преобразования Фурье в смысле обобщенных функций. В приводившихся выше определениях функции, входящие в пространство основных, были действительными. При определении преобразования Фурье целесообразно в качестве основных рассмотреть комплекснозначные функции.

Пусть K пространство комплексных основных функций (бесконечно дифференцируемых с финитным носителем).

Каждой комплекснозначной локально интегрируемой функции f(x) ставится в соответствие функционал

,

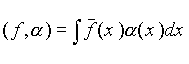комплексно сопряжена с f(x), a (x) Î K.

Множество всех линейных непрерывных функционалов на K образует комплексное пространство обобщенных функций K^/. Обозначим через Z - множество функций, являющихся преобразованиями Фурье функций из K.

Преобразованием Фурье элемента f из пространства K называется функционал g на пространстве Z, действующий по формуле

(g, y ) = 2 p (f, a ), (2.2.7)

здесь j такой элемент из K, для которого преобразование Фурье есть y . То есть для того чтобы вычислить действие функционала g на функцию y (l ) из пространства Z, нужно:

найти такую функцию a (x) из пространства K, преобразованием Фурье, которой является функция y (l );

найти действие функционала f на найденную функцию a (x).

Пространства основных функций и функционалов над ними выбраны нами так, что оба шага всегда выполнимы.

Здесь следует обратить внимание на то, что обобщенные функции и их преобразования Фурье определяются как линейные функционалы над разными основными пространствами. Причем функции из множества Z, на котором действуют преобразования Фурье, не являются функциями с финитными носителями, но продолжают оставаться бесконечно дифференцируемым. Что позволяет сохранить многие полезные свойства обобщенных функций.

В формулах обращения лучевого преобразования, на которых основаны алгоритмы решения задачах трехмерной компьютерной томографии, используется преобразование Фурье однородных функций. Классическое преобразование Фурье таких функций не существует, преобразование Фурье в формулах понимается в смысле обобщенных функций.

Рассмотрим несколько подробнее этот вопрос с точки зрения возможности построения соответствующих численных алгоритмов в трехмерном пространстве.

Напомним определение лучевого преобразования, которое было дано в предыдущих параграфах.

Лучевым преобразованием функции f(x) = f(x₁, x₂, x₃) называется функция

, (2.2.8)

являющаяся интегралом от f(x) вдоль луча, исходящего из точки S = (s₁, s₂, s₃) в направлении вектора a = (a ₁, a ₂, a ₃).

Как уже отмечалось выше, в наряду с функцией рассматривается функция

,

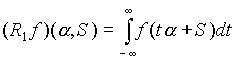являющаяся интегралом по всей прямой или, что тоже самое, суммой интегралов вдоль лучей из точки S в направлениях a и - a .

Обе функции являются однородными степени -1, то есть для них выполняются равенства

, .

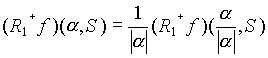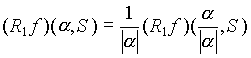Отметим также, что является четной, а функция таковой не является.

Понятие однородности степени l можно естественным образом расширить на обобщенные функции, если взять за основу равенство g(g x) = g l g(x). В терминах действия на основную функцию j равенство запишется в виде (g, j (x/g ) = g l ⁺ⁿ (g, j (x)), здесь g v любое вещественное число большее нуля, n n - размерность пространства, в котором заданы основные функции. В интегральном представлении обобщенных функций показатель n возникает при соответствующей замене переменных в dx.

Известно, что преобразование Фурье однородной обобщенной функции, тоже является однородной обобщенной функцией.

Для интегрируемых, ограниченных и имеющих ограниченный носитель, функций f их лучевое преобразование является регулярной однородной функцией. Из результатов работ следует, что в трехмерном пространстве преобразование Фурье таких функций, понимаемое в обобщенном смысле, задается регулярной функцией. Регулярная однородная функция задается своими значениями на единичной сфере. Таким образом, в практических ситуациях при инвертировании лучевого преобразования нас интересует соотношение между двумя функциями. Одна из них является сужением на единичную сферу лучевого преобразования, а другая - сужением на единичную сферу преобразование Фурье лучевых данных, понимаемого в смысле обобщенных функций. Подобное преобразование между функциями, заданными на единичной сфере естественно назвать преобразованием Семянистого, поскольку в его работе впервые получены подобные соотношения для симметричных однородных функций в n-мерных пространствах. Как уже отмечалось выше, функция не является симметричной, для нее соответствующие соотношения для функций на единичных сферах в трехмерном пространстве были получены в предыдущих параграфах.

Ранее были рассмотрены формулы обращения лучевого преобразования, основанные на явном использовании обобщенных функций, и приемы, позволяющие приводить эти формулы к виду удобному для построения численных алгоритмов.

К выводу формул обращения лучевого преобразования есть другой подход, не использующий обобщенные функции в явном виде. Мы покажем здесь, что фактически этот метод тоже основан на использовании преобразования Фурье в смысле обобщенных функций.

Лучевыми данными называется функция

,

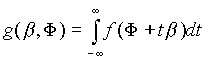Ф = (Ф₁, Ф₂, Ф₃) Î R³, b Î S² (S² v единичная сфера). (Не трудно видеть, что в наших обозначениях это функция ).

В формулах обращения используются следующие функции:

(2.2.9)

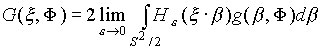, (2.2.10)

(S²/2 - половина единичной сферы), - скалярное произведение векторов и .

Формулы обращения в имеет вид

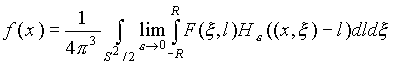, (2.2.11)

где , R v радиус шара, в котором содержится носитель функции f(х), -элемент поверхности на единичной сфере.

Если для любого l, такого, что ½ l½ < R и любого b Î S²/2 существует точка Ф на траектории источника такая, что Ф × b = l (выполняются условия Кириллова-Туя), то формула (2.2.11) может быть использована для определения функции f(х).

В отмечается, что функция F при трехмерной томографической реконструкции в конусе лучей в определенной степени аналогична роли преобразования Фурье в двумерной томографии. Этот факт не является случайным.

Действительно, в показано, преобразование Фурье по b в смысле обобщенных функций от функции g(b , Ф) имеет вид

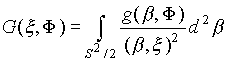. (2.2.12)

Знаменатель в (2.2.12) может быть равен нулю, и (2.2.12) следует понимать в смысле обобщенных функций. В доказано следующее утверждение.

Если f j Î C², то

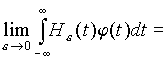
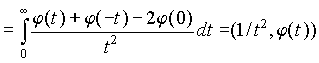. (2.2.13)

Учитывая (2.2.13), (2.2.12) и (2.2.10) мы видим, что функция , является преобразованием Фурье в смысле обобщенных функций функции g(b , F ), а функция F в формуле обращения определяется функцией .

Похожие работы

Цифровые методы рентгенодиагностики

Скачать

50528

0

0

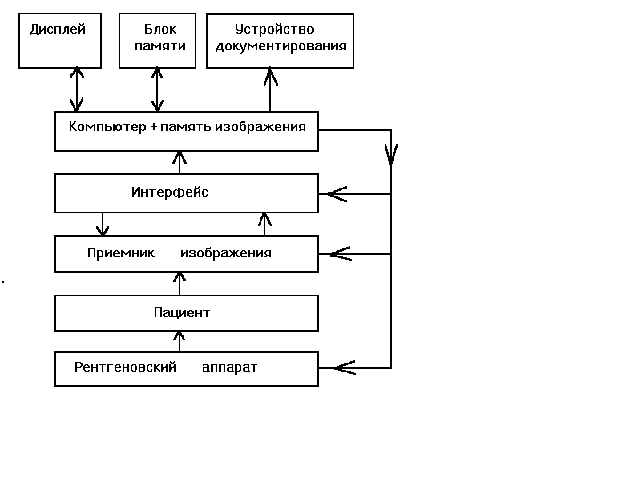
... более дорогостоящими, нежели обычные рентгеновские системы, однако по мере развития компьютерной техники и систем визуализации находят все более широкое применение. Цифровая рентгенодиагностика обеспечивается компьютерной технологией.Дисплей Блок долговременной памяти Устройство документирования Компьютер + память изображенияИнтерфейс данныхПриемник изображения Пациент Рентгеновский аппарат ...

Цифровая рентгенография

Скачать

33118

0

7

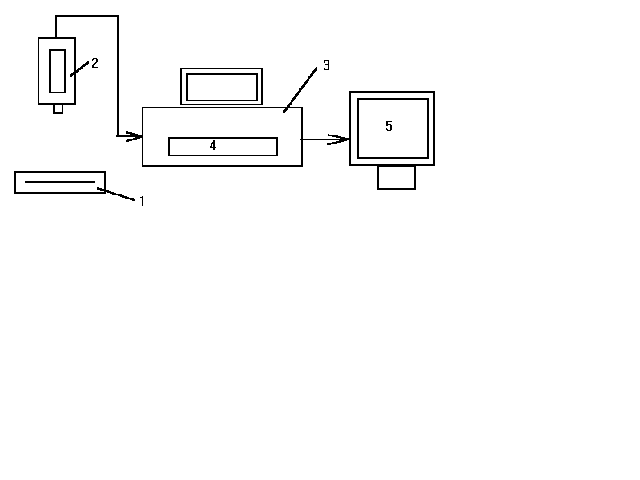
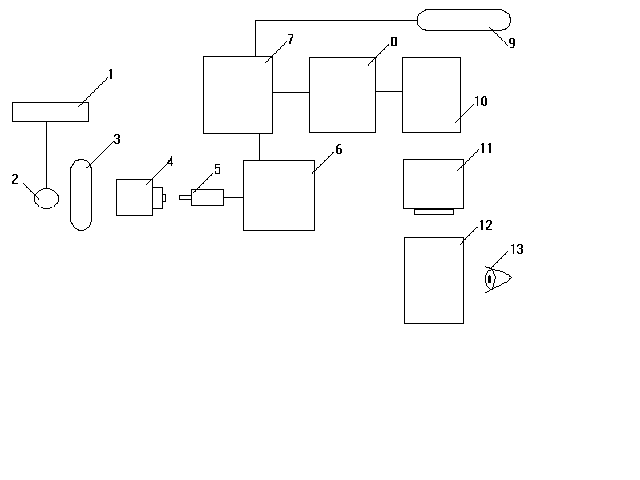
... обычная система электронно-оптического преобразования для просвечивания, из ЭОП, телевизионного тракта с высоким разрешением, рентгеновского высоковольтного генератора и рентгеновского излучателя Рис.5 Цифровая рентгенография с экрана ЭОП 1-генератор; 2-рентгеновская трубка; 3-пациент; 4-ЭОП; 5-видеокамера; 6-аналого-цифровой преобразователь; 7-накопитель изображений; 8-видеопроцессор; 9-сеть; ...

Основные платформы ЭВМ

Скачать

127846

0

0

... банковских систем. Наиболее популярны сегодня смешанные решения, при которых часть модулей банковской системы разрабатывается компьютерным отделом банка, а часть покупается у независимых производителей. Основными платформами для банковских систем в настоящее время считаются: 1. ЛВС на базе сервера PC (10,7%); 2. Различные модели специализированных бизнес-компьютеров фирмы IBM типа AS/400 ...