Сглаживание поворотов

2.2 Сглаживание поворотов.

По окончании первичного планирования траектории (п 2.1) мы будем иметь предварительную траекторию, представляющую собой ломанную, каждое из звеньев которой повёрнуто на угол с45⁰ относительно предыдущего звена. Данная траектория имеет низкое качество по сравнению с достижимой, поэтому требуется произвести сглаживание («срезание углов»). Именно это и будет выполнятся при вторичном планировании.

В целях экономии времени, алгоритм сглаживания будет запускаться для ближайшего поворота (как исключение и для следующего). При сглаживании программа будет пытаться провести траекторию между любыми двумя точками до начала ближайшего поворота и после его окончания. Для повышения быстродействия программа начнёт с минимального сглаживания (малое удачное сглаживание более вероятно), а затем попытается удлинить отрезок сглаживания. Попытки «срезать угол» будут прекращены как только исчезнет возможность осуществить сглаживание. Отрезок сглаживания будет проводится через клетки на которых возможно нахождение центра самосвала и ориентация самосвала в любом направлении.

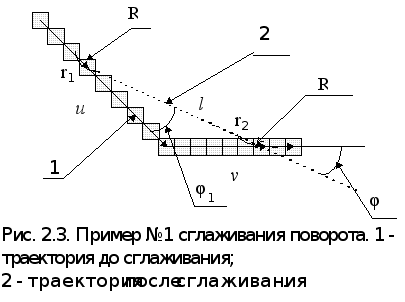
В результате удачного сглаживания (рис.2.3 - 2.5), вместо поворотов на с45⁰ возникнут два поворота на угол менее 45⁰ и отрезок сглаживания, длина которого будет меньше суммарной длины всех частей ломанной, расположенных между концами отрезка сглаживания. В связи с тем, что в программу, выполняющую первую стадию планирования не заложены повороты на эти углы (j₁ и j₂), алгоритм сглаживания по формулам должен будет определить точку начала поворота (r₁ и r₂). Указанные на рис. 3.3 величины найдём по формулам 2.1 - 2.5.

(2.1);

j₁=arccos (2.2);

j₂=arccos (2.3);

r₁=R*tg(j₁/2) (2.4);

r₂=R*tg(j₂/2) (2.5).

В случае поворота, изображенного на рисунке 2.4, величины, его определяющие, рассчитаем по формуле 2.6 и 2.7:

j=arctg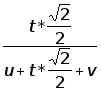 (2.6)

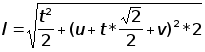(2.7).

Как в первом, так и во втором случаях линия l проводится таким образом, чтобы она не проходила через клетки, на которые запрещён въезд самосвала. В случае для рисунка 2.6 по формулам 2.8 и 2.9: (2.8);

j=arctg (2.9).

Возможна ситуация, когда конец сглаживания поворота совпадает с началом сглаживания следующего поворота (рис 2.6). В этом случае угол (j₅) между отрезками сглаживания l₁ и l₂ вычисляется по формуле 2.7, а упреждение поворота по формуле 2.4 (2.5), но с j₅ вместо j₂ ,

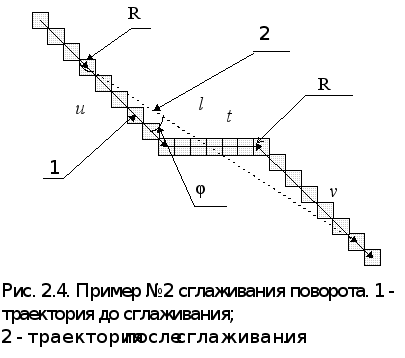
В случае, если сглаживание данного поворота произвести не удалось, то начинать поворот требуется на одну дискрету раньше точки излома на карте (при до поворота движении параллельно осям

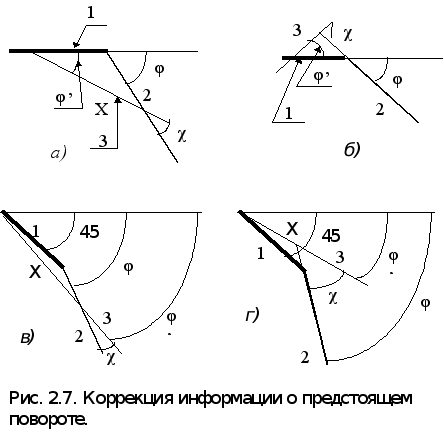
координат), и на три дискреты раньше при движении до поворота под углом к осям. Таким образом r_парр =1,875м (округлим до 2 м), а r_{подуглом} =4,375 м (округлим до 4,5 м). В связи с тем, что реальная ориентация самосвала перед сглаживанием будет отличаться от фиксированной, требуется корректировать углы на которые должен повернуть самосвал и расстояния которые он должен проехать до поворота, что бы выйти на най денный отрезок сглаживания. В приведённых ниже рисунках (2.7 а, б, в, г) и формулах введены следующие обозначения: j’ - угол между направлениями планируемом до поворота траектории и реальной ориентацией самосвала; j - угол между направлением планируемой траектории и отрезком сглаживания; c - угол между реальным направлением самосвала и отрезком сглаживания; х - реальное расстояние до поворота; k - количество дискрет до излома; d -длина одной дискреты. Методика выбора формулы для расчёта данных коррекции приведена в таблице 2.1.

В отличие от алгоритма первичного планирования траектории (п. 2.1), алгоритм сглаживания поворотов должен быть реализован на языках высокого уровня, располагающими библиотеками математических функций и позволяющих выполнять действия над данными разных типов.

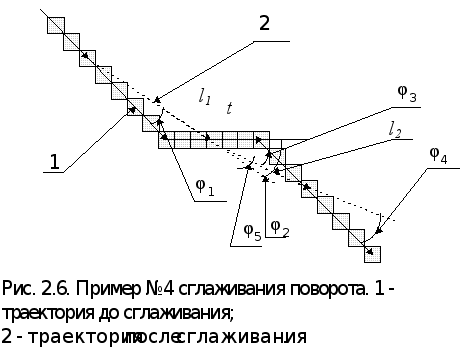
Таблица 2.1. Выбор расчётных формул для получения данных коррекции

Номер рисунка	Формула для вычисления c	Формула для вычисления х
2.8 а	c=j-j’	х=kd*sin(j)/sin(c)
2.8 б	c=j+j’	х=kd*sin(j)/sin(c)
2.8 в	c=j-j’	х=1.41*kd*sin(j+45)/sin(c)
2.8 г	c=j-j’	х=1.41*kd*sin(j-45)/sin(c)