МЕТОДЫ ТИПА СЦЕНАРИЕВ

2.4.2. МЕТОДЫ ТИПА СЦЕНАРИЕВ

Методы подготовки и согласования представлений о пробле­ме или анализируемом объекте, изложенные в письменном виде, получили название сценария. Первоначально этот метод предпо­лагал подготовку текста, содержащего логическую последова­тельность событий или возможные варианты решения проблемы, упорядоченные по времени. Однако требование временных ко­ординат позднее было снято, и сценарием стали называть любой документ, содержащий анализ рассматриваемой проблемы или предложения по ее решению независимо от того, в какой форме он представлен.

Сценарий не только предусматривает содержательные рассуж­дения, которые помогают не упустить детали, обычно не учиты­ваемые при формальном представлении системы (в этом и зак­лючалась первоначально основная роль сценария), но и содер­жит результаты количественного технико-экономического или статистического анализа с предварительными выводами, кото­рые можно получить на их основе. Группа экспертов, подготав­ливающих сценарии, пользуется правом получения необходимых справок от организаций, консультаций специалистов. Понятие сценариев расширяется в направлении как областей применения, так и форм представления и методов их разработки: в сценарий не только вводятся количественные параметры и устанавливаются

их взаимосвязи, но и предлагаются методики составления сцена­риев с использованием ЭВМ.

\ На практике по типу сценариев разрабатывались прогнозы в некоторых отраслях промышленности. В настоящее время раз-ндвидностью сценариев можно считать предложения к комплек­сным программам развития отраслей народного хозяйства, под-готавливаемыеt организациями или специальными комиссиями. Существенную помощь в подготовке сценариев оказывают спе­циалисты по системному анализу. Весьма перспективной пред­ставляется разработка специализированных информационно-поисковых систем, накапливающих прогнозную информацию по данной отрасли и по смежным отраслям.

Сценарий является предварительной информацией, на осно­ве которой проводится дальнейшая работа по прогнозированию или разработке вариантов проекта. Таким образом, сценарий помогает составить представление о проблеме, а затем присту­пить к более формализованному представлению системы в виде графиков, таблиц для проведения других методов системного анализа.

2.4.3. МЕТОДЫ ЭКСПЕРТНЫХ ОЦЕНОК

Группа методов экспертных оценок наиболее часто исполь­зуется в практике оценивания сложных систем на качественном уровне. Термин «эксперт» происходит от латинского слова expert - «опытный».

При использовании экспертных оценок обычно предполага­ется, что мнение группы экспертов надежнее, чем мнение отдель­ного эксперта. В некоторых теоретических исследованиях отме­чается, что это предположение не является очевидным, но одно­временно утверждается, что при соблюдении определенных требований в большинстве случаев групповые оценки надежнее индивидуальных. К числу таких требований относятся: распре­деление оценок, полученных от экспертов, должно быть «глад­ким»; две групповые оценки, данные двумя одинаковыми подгруппами, выбранными случайным образом, должны быть близки.

8—20

114

Глава 2

Основы оценки сложных систем

115

 

Все множество проблем, решаемых методами экспертных оценок, делится на два класса. К первому классу относятся та­кие, в отношении которых имеется достаточное обеспечение ин­формацией. При этом методы опроса и обработки основыва­ются на использовании принципа «хорошего измерителя», т.е. эксперт источник достоверной информации; групповое мне­ние экспертов близко к истинному решению. Ко второму клас­су относятся проблемы, в отношении которых знаний для уве­ренности и справедливости указанных гипотез недостаточно. В этом случае экспертов нельзя рассматривать как «хороших из­мерителей» и необходимо осторожно подходить к обработке результатов экспертизы.

Экспертные оценки несут в себе как узкосубъективные черты, присущие каждому эксперту, так и коллективно-субъективые, присущие коллегии экспертов. И если первые устраняются в про­цессе обработки индивидуальных экспертных оценок, то вторые не исчезают, какие бы способы обработки не применялись.

Этапы экспертизы формирование цели, разработка проце­дуры экспертизы, формирование группы экспертов, опрос, ана­лиз и обработка информации.

При формулировке цели экспертизы разработчик должен выработать четкое представление о том, кем и для каких целей будут использованы результаты.

При обработке материалов коллективной экспертной оценки используются методы теории ранговой корреляции. Для количе­ственной оценки степени согласованности мнений экспертов при­меняется коэффициент конкордации W, который позволяет оце­нить, насколько согласованы между собой ряды предпочтитель­ности, построенные каждым экспертом. Его значение находится в пределах 0 < W < I, где W = 0 означает полную противополож­ность, a W = 1 - полное совпадение ранжировок. Практически достоверность считается хорошей, если W = 0,7-0,8.

Небольшое значение коэффициента конкордации, свидетель­ствующее о слабой согласованности мнений экспертов, является следствием того, что в рассматриваемой совокупности экспер­тов действительно отсутствует общность мнений или внутри рас­сматриваемой совокупности экспертов существуют группы с вы­сокой согласованностью мнений, однако обобщенные мнения таких групп противоположны.

Для наглядности представления о степени согласованности мнений двух любых экспертов А и В служит коэффициент пар­ной ранговой корреляции р, он принимает значения -1 < р < +1. Значение р = +1 соответствует полному совпадению оценок в рангах двух экспертов (полная согласованность мнений двух экс­пертов), а значение р = -1 -двум взаимно противоположным ран­жировкам важности свойств (мнение одного эксперта противо­положно мнению другого).

Тип используемых процедур экспертизы зависит от задачи оценивания.

К наиболее употребительным процедурам экспертных изме­рений относятся:

•   ранжирование;

•   парное сравнивание;

•   множественные сравнения;

•   непосредственная оценка;

•   Черчмена-Акоффа;

•   метод Терстоуна;

•   метод фон Неймана-Моргенштерна.

Целесообразность применения того или иного метода во мно­гом определяется характером анализируемой информации. Если оправданы лишь качественные оценки объектов по некоторым качественным признакам, то используются методы ранжирова­ния, парного и множественного сравнения.

Если характер анализируемой информации таков, что целе­сообразно получить численные оценки объектов, то можно ис­пользовать какой-либо метод численной оценки, начиная от не­посредственных численных оценок и кончая более тонкими ме­тодами Терстоуна и фон Неймана-Моргенштерна.

При описании каждого из перечисленных методов будет пред­полагаться, что имеется конечное число измеряемых или оцени­ваемых альтернатив (объектов) А = {а^ ... ,а_п} и сформулирова­ны один или несколько признаков сравнения, по которым осу­ществляется сравнение свойств объектов. Следовательно, методы измерения будут различаться лишь процедурой сравнения объек­тов. Эта процедура включает построение отношений между объек­тами эмпирической системы, выбор преобразования ф и опреде­ление типа шкал измерений. С учетом изложенных выше обстоя­тельств рассмотрим каждый метод измерения. 8*

116

Глава 2

Основы оценки сложных систем

117

 

Ранжирование. Метод представляет собой процедуру упоря­дочения объектов, выполняемую экспертом. На основе знаний и опыта эксперт располагает объекты в порядке предпочтения, ру­ководствуясь одним или несколькими выбранными показателя­ми сравнения. В зависимости от вида отношений между объекта­ми возможны различные варианты упорядочения объектов.

Рассмотрим эти варианты. Пусть среди объектов нет одина­ковых по сравниваемым показателям, т.е. нет эквивалентных объектов. В этом случае между объектами существует только от­ношение строгого порядка. В результате сравнения всех объек­тов по отношению строгого порядка составляется упорядочен­ная последовательность а_{ > а₂> ... > a_N, где объект с первым номером является наиболее предпочтительным из всех объектов, объект со вторым номером менее предпочтителен, чем первый объект, но предпочтительнее всех остальных объектов и т.д. По­лученная система объектов с отношением строгого порядка при условии сравнимости всех объектов по этому отношению обра­зует полный строгий порядок. Для этого отношения доказано существование числовой системы, элементами которой являют­ся действительные числа, связанные между собой отношением неравенства >. Это означает, что упорядочению объектов соот­ветствует упорядочение чисел х, >... > x_n, где х,—ф Ц.). Возмож­на и обратная последовательность х, <... < x_n, в которой наибо­лее предпочтительному объекту приписывается наименьшее чис­ло и по мере убывания предпочтения объектам приписываются большие числа.

Соответствие перечисленных последовательностей, т.е. их гомоморфизм, можно осуществить, выбирая любые числовые представления. Единственным ограничением является монотон­ность преобразования. Следовательно, допустимое преобразова­ние при переходе от одного числового представления к другому должно обладать свойством монотонности. Таким свойством допустимого преобразования обладает шкала порядков, поэто­му ранжирование объектов есть измерение в порядковой шкале.

В практике ранжирования чаще всего применяется числовое представление последовательности в виде натуральных чисел:

т.е. используется числовая последовательность. Числа х,, х₂,..., x_n в этом случае называются рангами и обычно обозначаются

буквами г, , г₂, ... , r_N. Применение строгих численных отноше­ний «больше» (>), «меньше» (<) или «равно» (=) не всегда позво­ляет установить порядок между объектами. Поэтому наряду с ними используются отношения для определения большей или меньшей степени какого-то качественного признака (отношения частичного порядка, например полезности), отношения типа «более предпоч­тительно» (>), «менее предпочтительно» (<), «равноценно» ( = ) или «безразлично» (~). Упорядочение объектов при этом может иметь, например, следующий вид:

Такое упорядочение образует нестрогий линейный порядок.

Для отношения нестрогого линейного порядка доказано су­ществование числовой системы с отношениями неравенства и равенства между числами, описывающими свойства объектов. Любые две числовые системы для нестрогого линейного порядка связаны между собой монотонным преобразованием. Следова­тельно, ранжирование при условии наличия эквивалентных объек­тов представляет собой измерение также в порядковой шкале.

В практике ранжирования объектов, между которыми допус­каются отношения как строгого порядка, так и эквивалентности, числовое представление выбирается следующим образом. Наи­более предпочтительному объекту присваивается ранг, равный единице, второму по предпочтительности - ранг, равный двум, и т.д. Для эквивалентных объектов удобно с точки зрения техно­логии последующей обработки экспертных оценок назначать одинаковые ранги, равные среднеарифметическому значению рангов, присваиваемых одинаковым объектам. Такие ранги на­зывают связанными рангами. Для приведенного примера упо­рядочения на основе нестрогого линейного порядка при N = 10 ранги объектов д₃ , а₄ , а₅ будут равными г₃ = г₄ = г₅ = (3+4+5) /3 = 4.

В этом же примере ранги объектов й₉, а,₀ также одинаковы и равны среднеарифметическому r₉ = r_lo = (9+10) 12 = 9,5. Связан­ные ранги могут оказаться дробными числами. Удобство исполь­зования связанных рангов заключается в том, что сумма рангов N объектов равна сумме натуральных чисел от единицы до N. При этом любые комбинации связанных рангов не изменяют эту сумму. Данное обстоятельство существенно упрощает обработ­ку результатов ранжирования при групповой экспертной оценке.

118

Глава 2

Основы оценки сложных систем

119

 

 

При групповом ранжировании каждый S-й эксперт присваи­вает каждому /-му объекту ранг r_js. В результате проведения экс­пертизы получается матрица рангов | | r_is \ \ размерности Nk, где k- число экспертов; N- число объектов; S=l,k;i=l,N. Результа­ты группового экспертного ранжирования удобно представить в виде табл. 2.5.

Аналогичный вид имеет таблица, если осуществляется ран­жирование объектов одним экспертом по нескольким показате­лям сравнения. При этом в таблице вместо экспертов в соответ­ствующих графах указываются показатели. Напомним, что ран­ги объектов определяют только порядок расположения объектов по показателям сравнения. Ранги как числа не дают возможнос­ти сделать вывод о том, на сколько или во сколько раз предпоч­тительнее один объект по сравнению с другим.

Таблица 2.5

Результаты группового ранжирования

Объект	э,	Э2	...	э*
Й1	г\\	'12	...	r\k
«2	Г21	'22	...	r2k
...	...	...
ап	rnl	ГЛ	...	rnk

Достоинство ранжирования как метода экспертного изме­рения - простота осуществления процедур, не требующая трудо­емкого обучения экспертов. Недостатком ранжирования явля­ется практическая невозможность упорядочения большого чис­ла объектов. Как показывает опыт, при числе объектов, большем 10-15, эксперты затрудняются в построении ранжировки. Это объясняется тем, что в процессе ранжирования эксперт должен установить взаимосвязь между всеми объектами, рассматривая их как единую совокупность. При увеличении числа объектов количество связей между ними растет пропорционально квадра­ту числа объектов. Сохранение в памяти и анализ большой сово­купности взаимосвязей между объектами ограничиваются пси­хологическими возможностями человека. Психология утвержда-

ет, что оперативная память человека позволяет оперировать в среднем не более чем 7 ± 2 объектами одновременно. Поэтому при ранжировании большого числа объектов эксперты могут допускать существенные ошибки.

Парное сравнение. Этот метод представляет собой процедуру установления предпочтения объектов при сравнении всех возмож­ных пар. В отличие от ранжирования, в котором осуществляется упорядочение всех объектов, парное сравнение объектов являет­ся более простой задачей. При сравнении пары объектов возмож­но либо отношение строгого порядка, либо отношение эквива­лентности. Отсюда следует, что парное сравнение так же, как и ранжирование, есть измерение в порядковой шкале.

В результате сравнения пары объектов а_;, а/ эксперт упоря­дочивает ее, высказывая либо я, >- а-, либо а, > a_t, либо a_t ~ а . Выбор числового представления ф(й₍.) можно произвести так: если a_i X а» то ф (а₍.) > ф (о ); если предпочтение в паре обратное, то знак неравенства заменяется на обратный, т.е. ф (а,) < ф (а,). Если объекты эквивалентны, то можно считать, что ф (я,-) = ф (а ).

В практике парного сравнения используются следующие чис­ловые представления:

(2.1)

Хн = •

(

I, если а/ >- dj или a_t ~ Oj\ О, если а, ч о/, i,j = l,N;

(2.2)

2, если а,- >- а_у-; 1, если а,- ~ uji О, если а; ч а .•, /, J = 1, N.

Результаты сравнения всех пар объектов удобно представлять в виде матрицы. Пусть, например, имеются пять объектов а,, а₂, а₃, а₄, а₅ и проведено парное сравнение этих объектов по пред­почтительности. Результаты сравнения представлены в виде

Используя числовое представление (2.1), составим матрицу измерения результатов парных сравнений (табл. 2.6).

120

Глава 2

Основы оценки сложных систем

121

 

Таблица 2.7

Таблица 2.6

Результаты измерения пяти объектов

	а\	°2	аз	Й4	°5
а\	\	2	2	2	0
°2	0	1	2	2	0
Й3	0	0	1	1	0
«4	0	0	1	1	0
°5	2	2	2	2	1

Матрица парных сравнений

	«1	°2	аЗ	°4	а5
«1	1	1	1	1	0
а2	0	1	1	1	0
аз	0	0	1	1	0
а4	0	0	1	1	0
°5	1	1	1	1	1

В табл. 2.6 на диагонали всегда будут расположены единицы, поскольку объект эквивалентен себе. Представление (2.2) харак­терно для отображения результатов спортивных состязаний. За выигрыш даются два очка, за ничью одно и за проигрыш ноль очков (футбол, хоккей и т.п.). Предпочтительность одного объек­та перед другим трактуется в данном случае как выигрыш одно­го участника турнира у другого. Таблица результатов измерения при использовании числового представления не отличается от таблиц результатов спортивных турниров за исключением диа­гональных элементов (обычно в турнирных таблицах диагональ­ные элементы заштрихованы). В качестве примера в табл. 2.7 при­ведены результаты измерения пяти объектов с использованием представления (2.2), соответствующие табл. 2.6.

Вместо представления (2.2) часто используют эквивалентное ему представление

хн -1

+ 1, если cn>aj', О, если ai~dj', -1, если ai^aj-, i,j = l,N,

которое получается из (2.2) заменой 2 на +1, 1 на 0 и 0 на 1.

Если сравнение пар объектов производится отдельно по раз­личным показателям или сравнение осуществляет группа экспер­тов, то по каждому показателю или эксперту составляется своя таблица результатов парных сравнений. Сравнение во всех воз-

можных парах не дает полного упорядочения объектов, поэтому возникает задача ранжирования объектов по результатам их пар­ного сравнения.

Однако, как показывает опыт, эксперт далеко не всегда пос­ледователен в своих предпочтениях. В результате использования метода парных сравнений эксперт может указать, что объект а, предпочтительнее объекта а₂, а₂ предпочтительнее объекта а₃ и в то же время а₃ предпочтительнее объекта а,.

В случае разбиения объекта на классы эксперт может к одно­му классу отнести пары a_l и а₂, а₂ и а₃, но в то же время объекты а, и а₃ отнести к различным классам. Такая непоследовательность эксперта может объясняться различными причинами: сложнос­тью задачи, неочевидностью предпочтительности объектов или разбиения их на классы (в противном случае, когда все очевид­но, проведение экспертизы необязательно), недостаточной ком­петентностью эксперта, недостаточно четкой постановкой зада­чи, многокритериальностью рассматриваемых объектов и т.д.

Непоследовательность эксперта приводит к тому, что в ре­зультате парных сравнений при определении сравнительной пред­почтительности объектов мы не получаем ранжирования и даже отношений частичного порядка не выполнено свойство транзи­тивности.

Если целью экспертизы при определении сравнительной пред­почтительности объектов является получение ранжирования или частичного упорядочения, необходима их дополнительная иден­тификация. В этих случаях имеет смысл в качестве результирую­щего отношения выбирать отношение заданного типа, ближай­шее к полученному в эксперименте.

Множественные сравнения. Они отличаются от парных тем, что экспертам последовательно предъявляются не пары, а трой­ки, четверки,..., n-ки («<ЛО объектов. Эксперт их упорядочивает по важности или разбивает на классы в зависимости от целей эк­спертизы. Множественные сравнения занимают промежуточное положение между парными сравнениями и ранжированием. С одной стороны, они позволяют использовать больший, чем при парных сравнениях, объем информации для определения экспер­тного суждения в результате одновременного соотнесения объек­та не с одним, а с большим числом объектов. С другой стороны, при ранжировании объектов их может оказаться слишком мно-

122

Глава 2

Основы оценки сложных систем

123

 

 

го, что затрудняет работу эксперта и сказывается на качестве ре­зультатов экспертизы. В этом случае множественные сравнения позволяют уменьшить до разумных пределов объем поступаю­щей к эксперту информации.

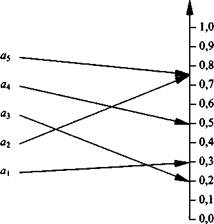
Непосредственная оценка. Метод заключается в присваивании объектам числовых значений в шкале интервалов. Эксперту не­обходимо поставить в соответствие каждому объекту точку на определенном отрезке числовой оси. При этом необходимо, что­бы эквивалентным объектам приписывались одинаковые числа. На рис. 2.6 в качестве примера приведено такое представление для пяти объектов на отрезок числовой оси [0,1].

Поскольку за начало отсчета выбрана нулевая точка, то в дан­ном примере измерение производится в шкале отношений. Экс­перт соединяет каждый объект линией с точкой числовой оси и получает следующие числовые представления объектов (см. рис. 2.6):

Ф (а,) = 0,28; <р (а₂) = <р (а₅) = 0,75; ф (а₃) = 0,2; ф (aj = 0,5.

Оцениваемые объекты

Шкала отношений

Рис. 2.6. Пример сравнения пяти объектов по шкале

Измерения в шкале интервалов могут быть достаточно точ­ными при полной информированности экспертов о свойствах объектов. Эти условия на практике встречаются редко, поэтому для измерения применяют балльную оценку. При этом вместо

непрерывного отрезка числовой оси рассматривают участки, ко­торым приписываются баллы.

Эксперт, приписывая объекту балл, тем самым измеряет его с точностью до определенного отрезка числовой оси. Применя­ются 5-, 10- и 100-балльные шкалы.

Метод Черчмена Акоффа (последовательное сравнение). Этот метод относится к числу наиболее популярных при оценке аль­тернатив. В нем предполагается последовательная корректиров­ка оценок, указанных экспертами. Основные предположения, на которых основан метод, состоят в следующем:

•   каждой альтернативе a_t(i = \,N) ставится в соответствие
действительное неотрицательное число ф (а_г );

•   если альтернатива a_i предпочтительнее альтернативы а, ,
то ф (а,.) > ф (а.), если же альтернативы я_г и я равноценны,
тоф(о₍.) = ф(а_/);

•   если ф (я,.) и ф (а .) оценки альтернатив а/ и а •, то ф (а₍.) + ф (а)
соответствует совместному осуществлению альтернатив а/ и а..
Наиболее сильным является последнее предположение об адди­
тивности оценок альтернатив.

Согласно методу Черчмена-Акоффа альтернативы a_t, a₂, ... , a_N ранжируются по предпочтительности. Пусть для удобства из­ложения альтернатива a_l наиболее предпочтительна, за ней сле­дует а₂ и т.д. Эксперт указывает предварительные численные оцен­ки ф (flj) для каждой из альтернатив. Иногда наиболее предпоч­тительной альтернативе приписывается оценка 1, остальные оценки располагаются между 0 и 1 в соответствии с их предпоч­тительностью. Затем эксперт производит сравнение альтернати­вы a_l и суммы альтернатив а₂, ••• > ^ан- Если а\ предпочтительнее, то эксперт корректирует оценки так, чтобы

N

В противном случае должно выполняться неравенство

Если альтернатива а_; оказывается менее предпочтительной, то для уточнения оценок она сравнивается по предпочтению с суммой альтернатив а₂,а₃, ... , a_N_, и т.д. После того как альтер-

124

Глава 2

 

 

\pat;, (1-р)а/] предпочтительнее, чем \р'а{, (1-р') в/], если/»/?' и др. Если указанная система предпочтений выполнена, то для каж­дой из набора основных альтернатив al , а2, ... , aN определяют­ся числа jf], х2, ... , xn, характеризующие численную оценку сме­шанных альтернатив. Численная оценка смешанной альтернативы \pl alt р2а2, ... , PN aN] равна х, />, + х2р2 + . . . + xNpN. Смешанная альтернатива \р^а^ р2а2, ... , pNaN] предпочтитель­нее смешанной альтернативы \р\ а,, р "2 аг , ... , p'N aN], если

натива a_l оказывается предпочтительнее суммы альтернатив а₂,..., a_k (к > 2), она исключается из рассмотрения, а вместо оцен­ки альтернативы а, рассматривается и корректируется оценка аль­тернативы я₂- Процесс продолжается до тех пор, пока откоррек­тированными не окажутся оценки всех альтернатив.

При достаточно большом N применение метода Черчмена-Акоффа становится слишком трудоемким. В этом случае целесо­образно разбить альтернативы на группы, а одну из альтерна­тив, например максимальную, включить во все группы. Это по­зволяет получить численные оценки всех альтернатив с помощью оценивания внутри каждой группы.

Метод Черчмена-Акоффа является одним самых эффектив­ных. Его можно успешно использовать при измерениях в шкале отношений. В этом случае определяется наиболее предпочтитель­ная альтернатива я₍₁. Ей присваивается максимальная оценка. Для всех остальных альтернатив эксперт указывает, во сколько раз они менее предпочтительны, чем а₍₁. Для корректировки числен­ных оценок альтернатив можно использовать как стандартную процедуру метода Черчмена-Акоффа, так и попарное сравнение предпочтительности альтернатив. Если численные оценки аль­тернатив не совпадают с представлением эксперта об их пред­почтительности, производится корректировка.

Метод фон Неймана—Моргенштерна. Он заключается в по­лучении численных оценок альтернатив с помощью так называ­емых вероятностных смесей. В основе метода лежит предполо­жение, согласно которому эксперт для любой альтернативы а-, менее предпочтительной, чем а₍, но более предпочтительной, чем a_t, может указать число а (0 <р < \) такое, что альтернатива а, эквивалентна смешанной альтернативе (вероятностной сме­си) [pa_t, (l-р) а/]. Смешанная альтернатива состоит в том, что альтернатива a_f выбирается с вероятностью Р, а альтернатива а_{ с вероятностью \-Р. Очевидно, что если Р достаточно близко к 1, то альтернатива Oj менее предпочтительна, чем смешанная аль­тернатива [pa_t, (\-p)a_t]. В литературе помимо упомянутого выше предположения рассматривается система предположений (акси­ом) о свойствах смешанных и несмешанных альтернатив. К чис­лу таких предположений относятся предположение о связности и транзитивности отношения предпочтительности альтернатив, предположение о том, что смешанная альтернатива

х₂р₂ + ... + x_Np_N > Xj/j + х₂р'₂ + ... +x_n p'_N .

Таким образом, устанавливается существование функции по­лезности

x_lPl+...+x_Np_N,

значение которой характеризует степень предпочтительности

любой смешанной альтернативы, в частности и несмешанной.

Более предпочтительна та смешанная альтернатива, для которой

значение функции полезности больше.

Рассмотренные выше методы экспертных оценок обладают

различными качествами, но приводят в общем случае к близким результатам. Практика применения этих методов показала, что наиболее эффективно комплексное применение различных мето­дов для решения одной и той же задачи. Сравнительный анализ результатов повышает обоснованность делаемых выводов. При этом следует учитывать, что методом, требующим минимальных затрат, является ранжирование, а наиболее трудоемким метод последовательного сравнения (Черчмена Акоффа). Метод пар­ного сравнения без дополнительной обработки не дает полного упорядочения объектов.