Основные понятия и определения

3.1 Основные понятия и определения

Надежность – свойство изделия (детали, компонента, элемента, узла, блока, устройства, системы) выполнять заданные функции (являться работоспособным) в течение требуемого промежутка времени.

Надежность современной электронной аппаратуры (ЭА) в значительной мере определяется надежностью составляющих ее компонентов, и границы сложности электронных систем зависят в основном от достижимого уровня надежности составляющих их технических средств. Проблема обеспечения надежности приобретает тем большее значение, чем сложнее ЭА. Разрешение противоречия между сложностью устройств и их надежностью является одной из важнейших инженерных задач.

В основе проектирования надежности ЭА лежит математическая теория надежности, опирающаяся на статистическую теорию надежности. Обработка статистических материалов в области надежности привела к накоплению большой статистической информации. Разработаны статистические характеристики и закономерности отказов ЭА. Теория надежности изучает природу и процессы возникновения отказов в технических системах, методы борьбы с этими отказами, вопросы прогнозирования состояния работоспособности систем.

Вероятность безотказной работы – вероятность того, что в заданном интервале времени не произойдет ни одного отказа.

Вероятность отказа – вероятность того, что в заданном интервале времени произойдет хотя бы один отказ.

Так как работоспособность и отказ являются несовместимыми событиями, то

. (3.1)

При экспериментальных исследованиях опытная вероятность безотказной работы (оценка вероятности) определяется из соотношения

, где (3.2)

– общее количество изделий одинакового типа при испытании на надежность;

– количество отказавших изделий на интервале времени .

Дифференцирование левой и правой частей соотношения (3.2) приводит к выражению

.

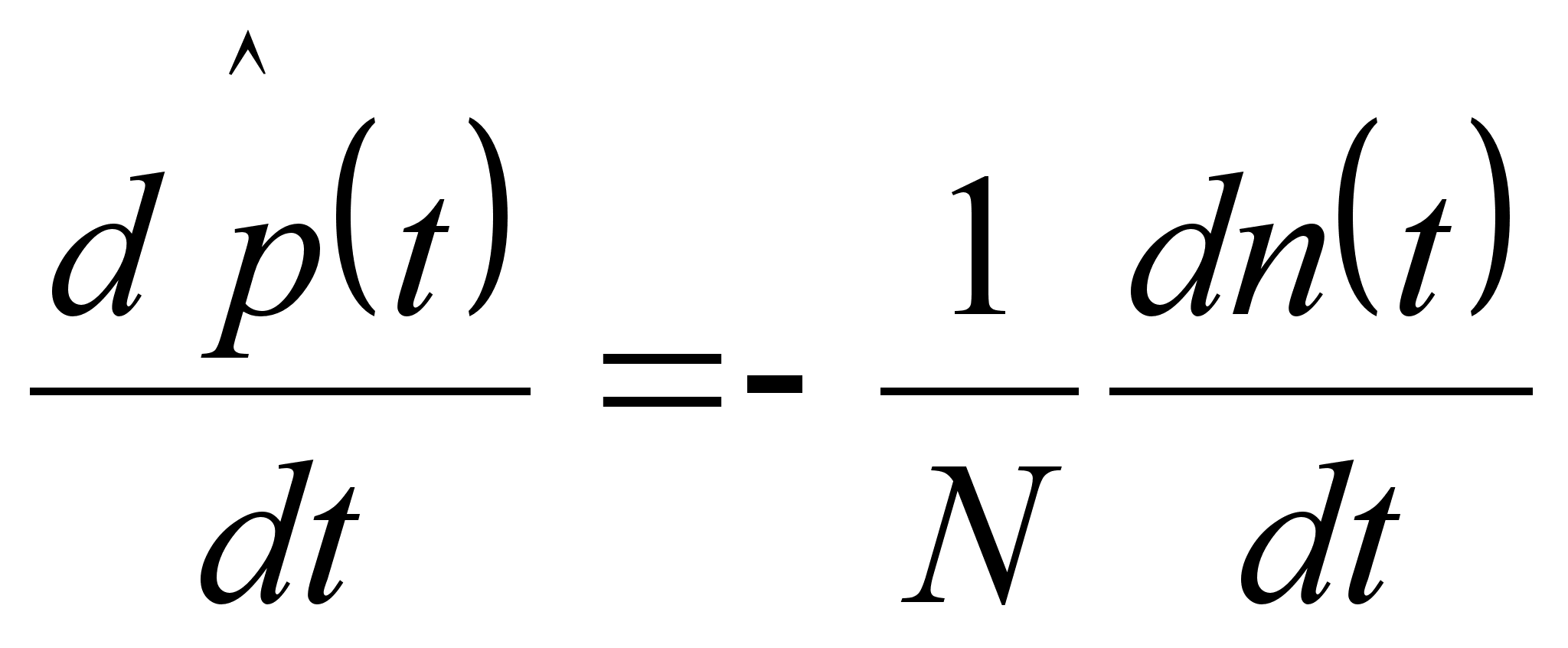Поделив обе части выражения на , получим

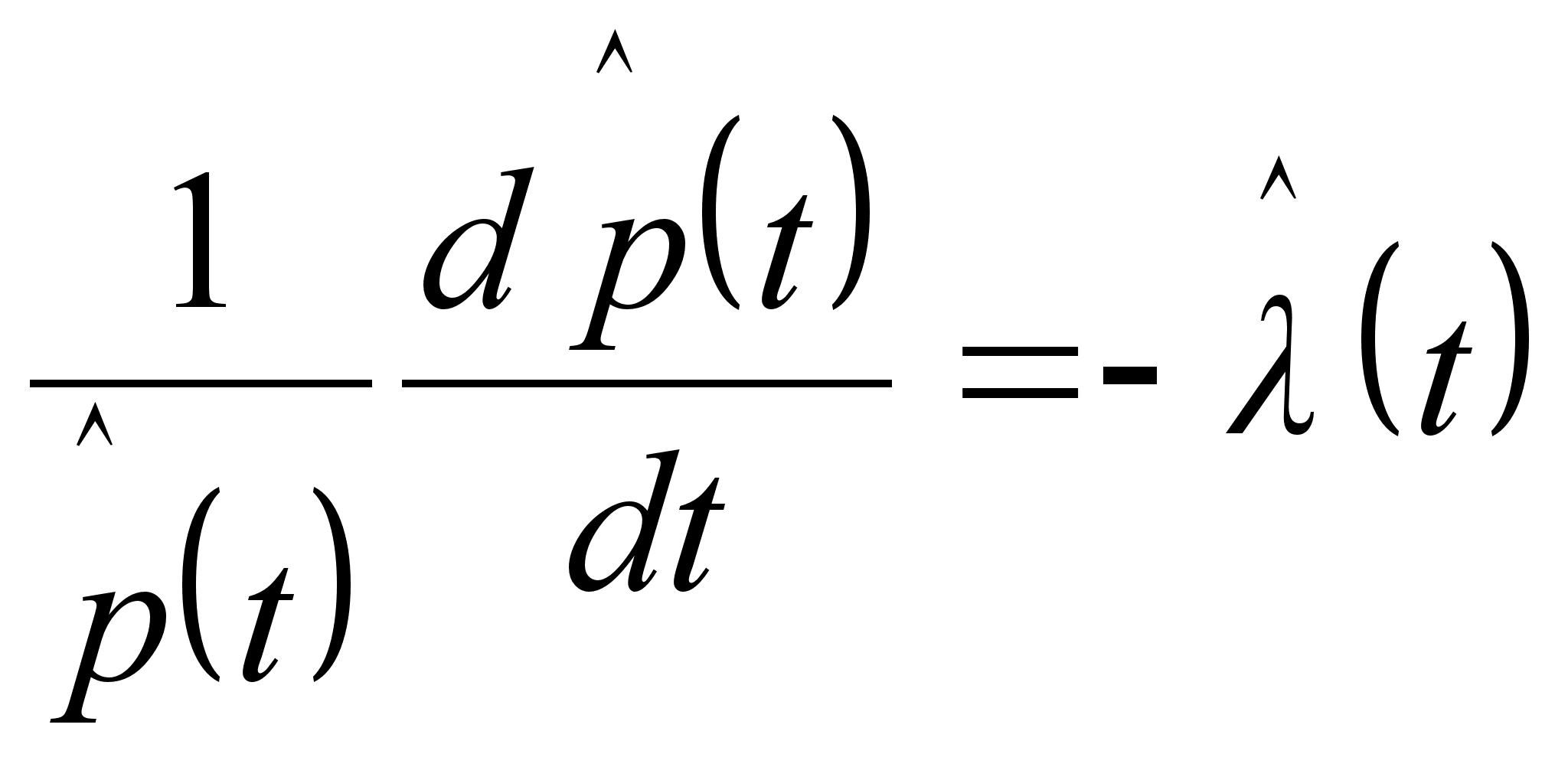, где

(3.3)

оценка интенсивности отказов изделия.

При увеличении количества изделий, участвующих в испытании на надежность до уровня оценки вероятности и интенсивности отказов стремятся к постоянным истинным значениям вероятности и интенсивности отказов . Поэтому получаем уравнение

.

Решение этого дифференциального уравнения находится интегрированием левой и правой частей уравнения с учетом того, что , имеем

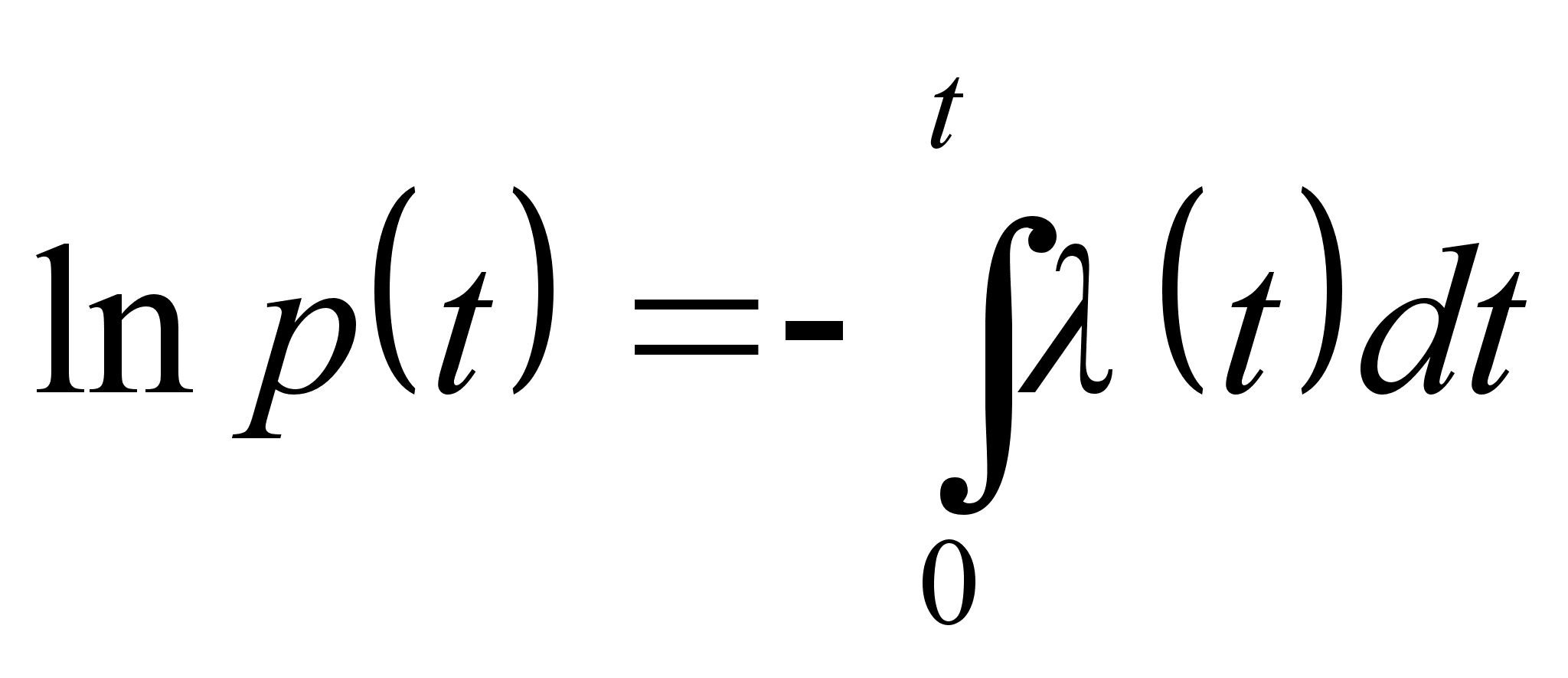
или .

На практике выполняется ограничение, когда не зависит от времени на достаточно большом интервале времени и равна . Тогда

. (3.4)

Это соотношение устанавливает связь вероятности безотказной работы изделия с интенсивностью отказов данного изделия .

Используя соотношение (3.1) и (3.4), получим

.

Определим плотность вероятности отказов изделия

, (3.5)

которая подчиняется экспоненциальному закону распределения. Для любого закона распределения отказов справедливы соотношения

, .

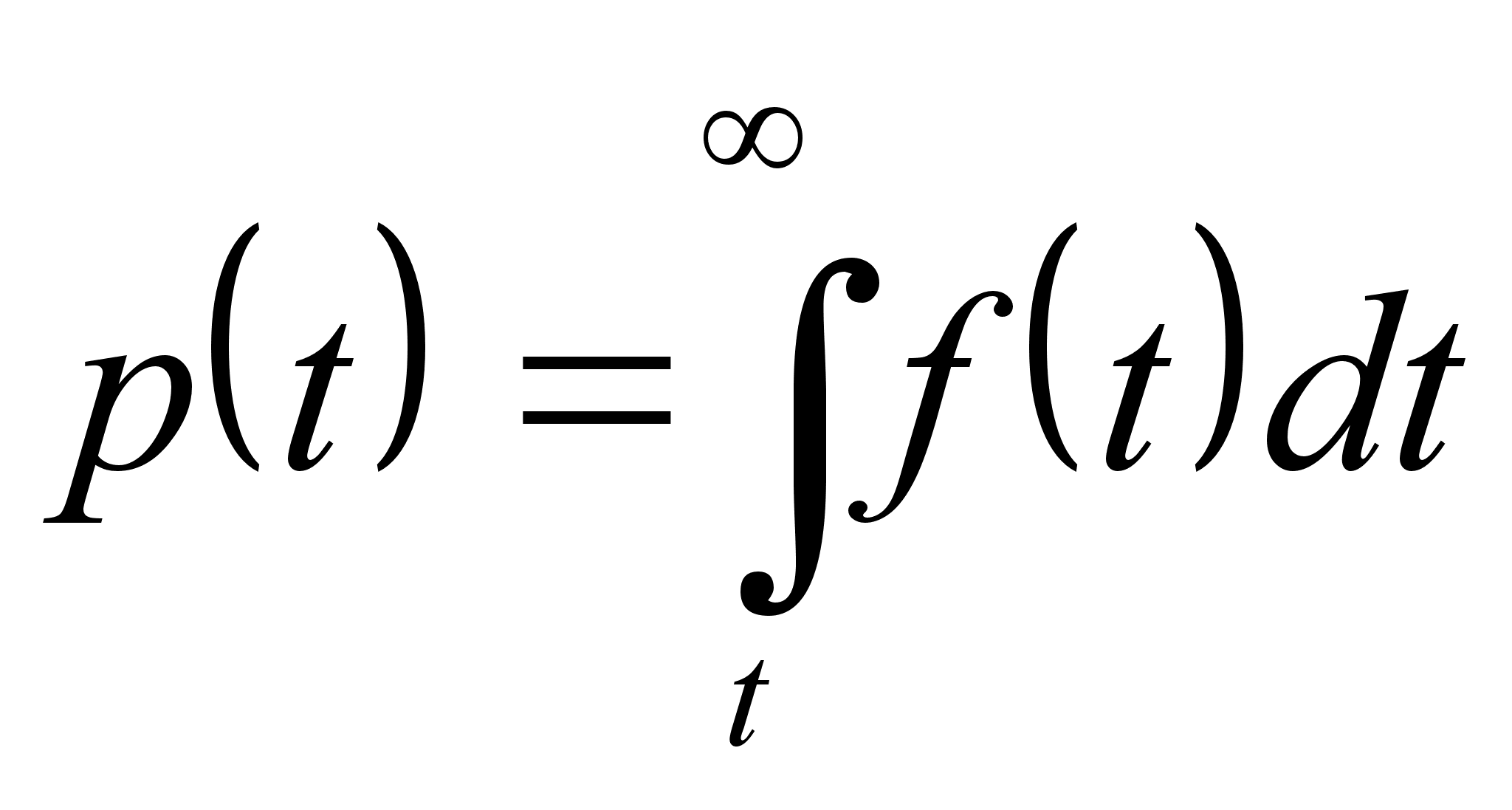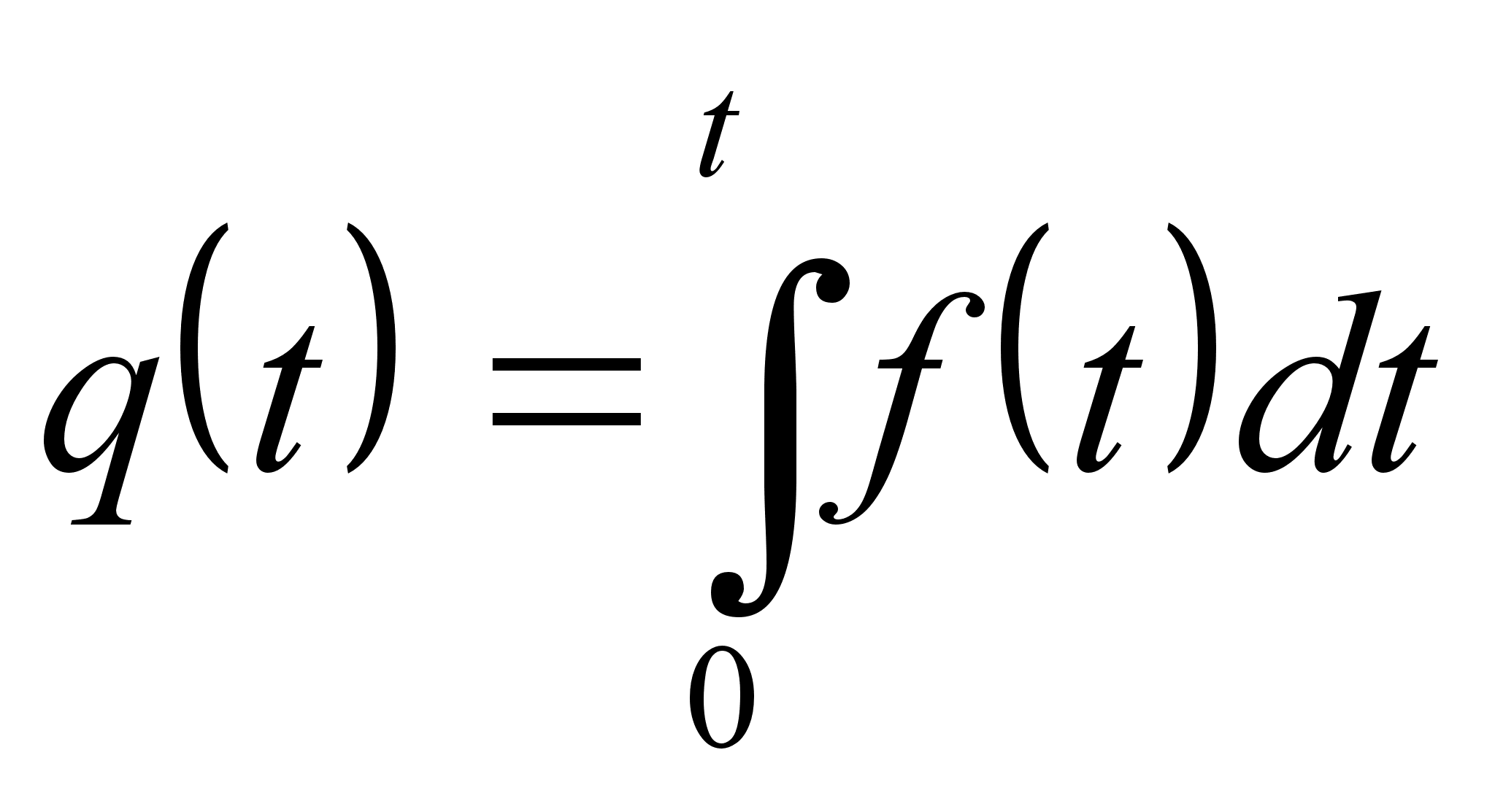В качестве показателя надежности ЭА используют только среднее время безотказной работы (математическое ожидание случайной величины )

.

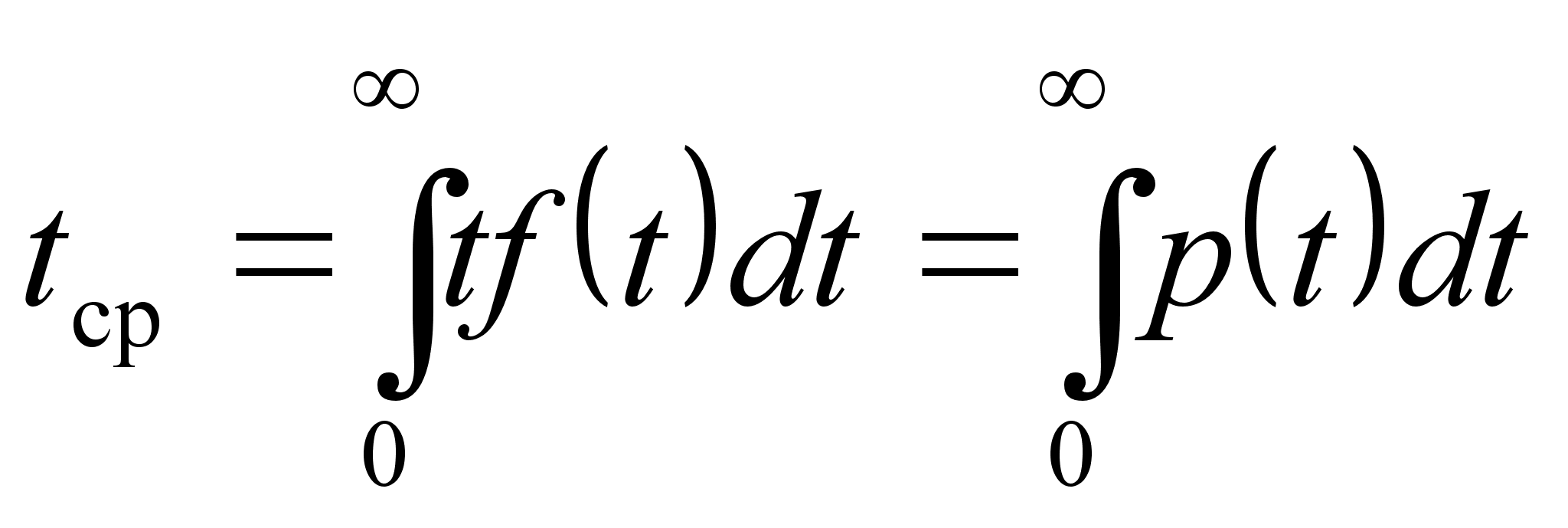Для экспоненциального закона распределения отказов (3.5)

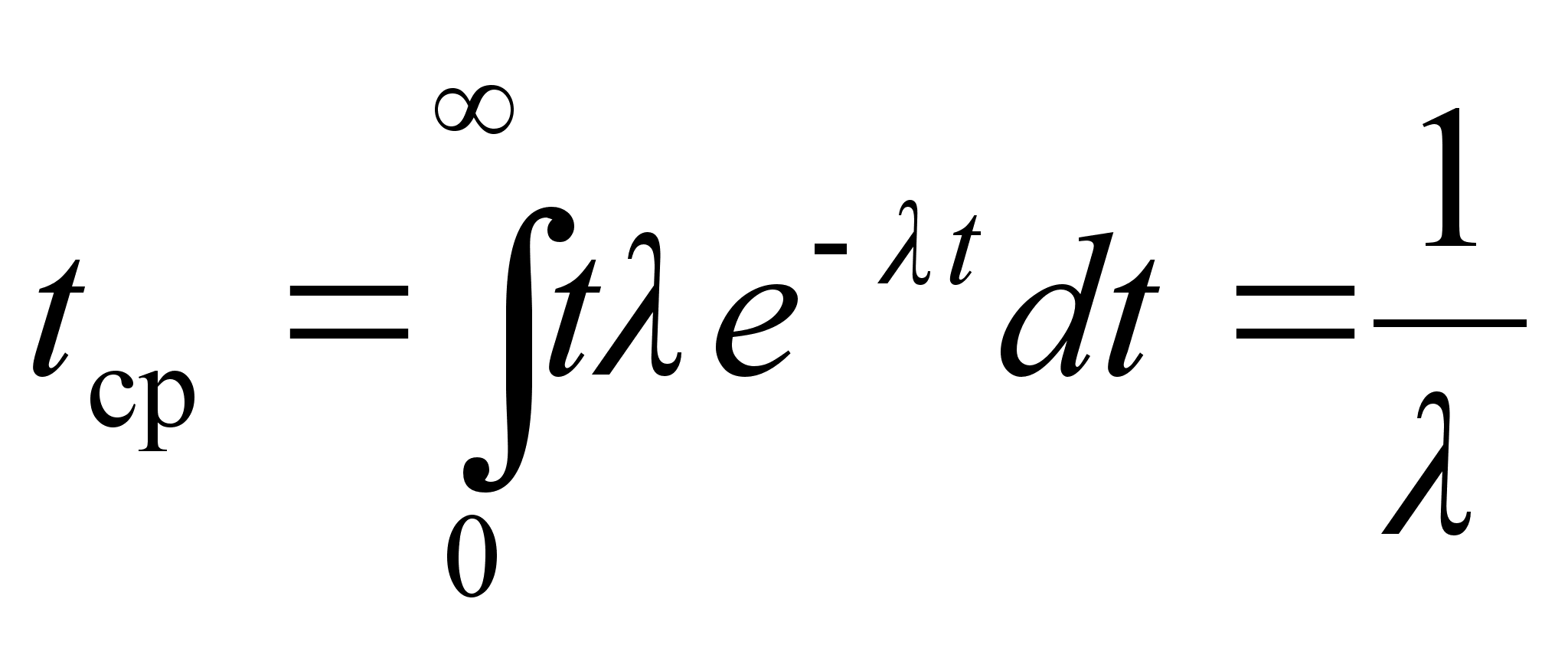. (3.6)

При экспериментальной оценку среднее время безотказной работы изделия определяется следующим образом

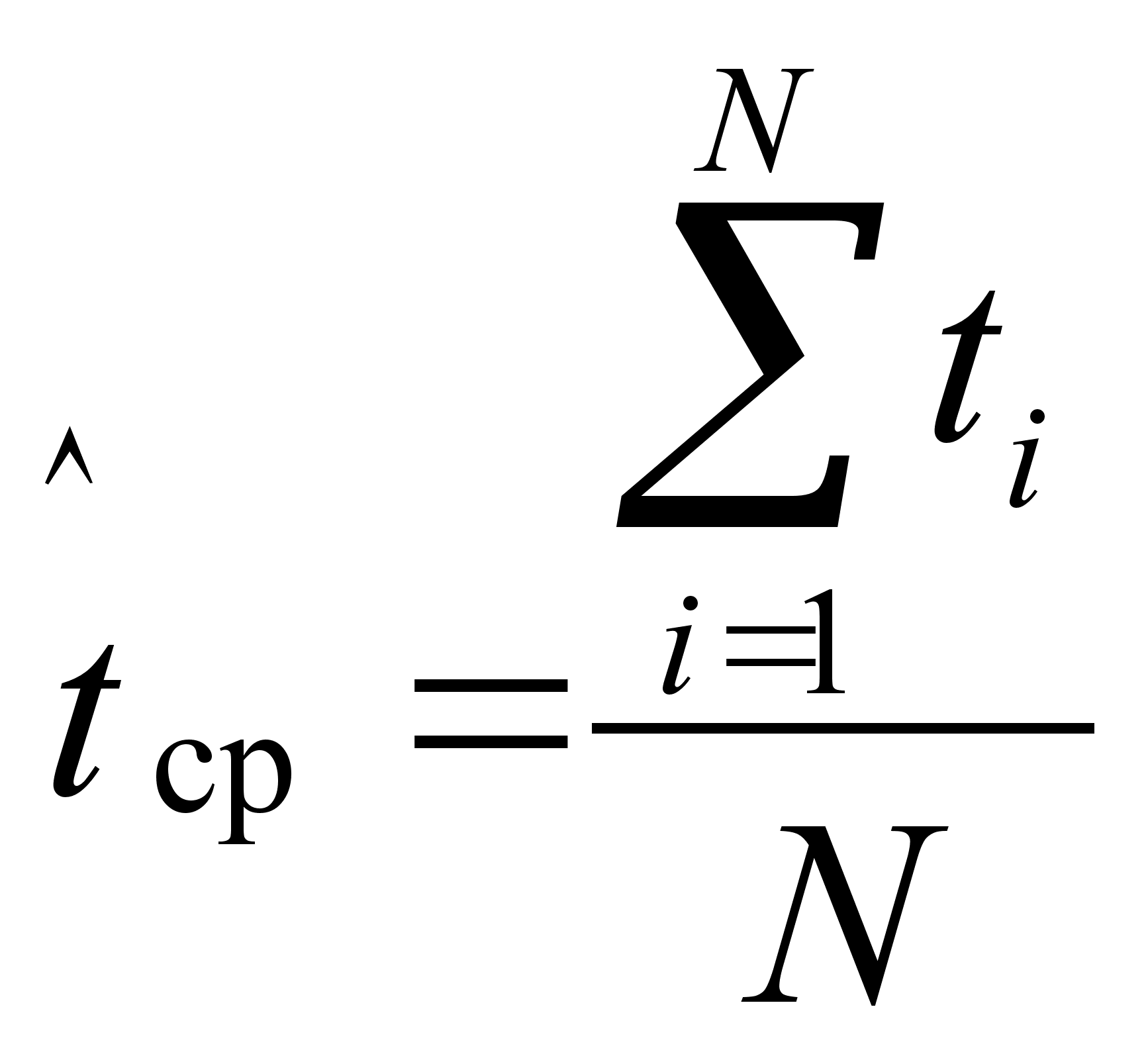, где

– время исправной работы i-го изделия,

– число изделий в партии, над которой производится испытание.

Используя соотношение (3.6) для вероятности безотказной работы (3.4) получим

.

Положим . Тогда , т.е. на интервале времени отказали 63% изделий и сохранили безотказность 37%.

Дисперсия времени безотказной работы определяется из выражения

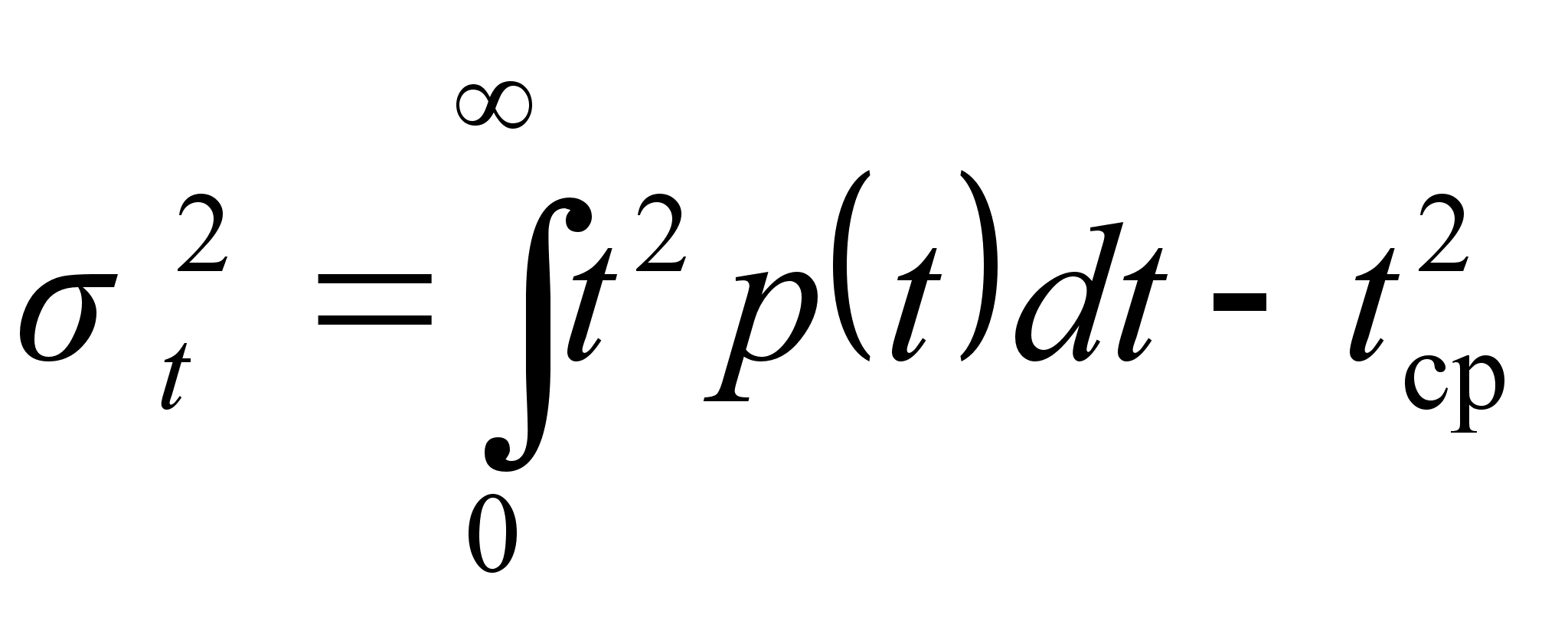
и при экспоненциальном законе распределения отказов равна

.

Отсюда среднеквадратическое отклонение времени безотказной работы изделия будет

.

Интенсивность отказов любого изделия определяется выражением (3.3). Для небольших интервалов времени справедливы приближения , , , поэтому из (3.3) имеем

.

Эта оценка интенсивности отказов может быть использована при опытном определении интенсивности отказов. Физически интенсивность отказов изделий определяет относительное число отказавших изделий в единицу времени. Единицей измерения интенсивности отказов обычно является величина .

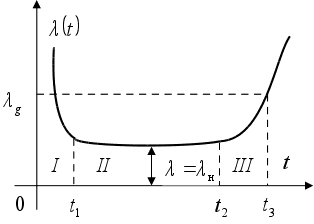
Интенсивность отказов изделия на большом интервале времени описывается качественной кривой (рис.4). Она характеризуется тремя явно выраженными периодами: приработки I, нормальной эксплуатации II и износа III.

На участке приработки наблюдаются внезапные приработочные отказы. Они возникают вследствие того, что часть элементов, входящих в состав изделия, являются либо бракованными, либо имеют низкий уровень надежности. Период приработки составляет обычно доли и единицы процента от времени нормальной эксплуатации изделия.

На втором участке интенсивность отказов изделия имеет минимальный, примерно постоянный номинальный уровень . Для этого периода работы изделия характерны внезапные отказы, вследствие действия ряда случайных факторов. Предупредить их приближение практически невозможно, тем более, что к этому времени в изделии остаются только полноценные компоненты, срок износа которых еще не наступил.

Рис.4 Зависимость интенсивности отказов изделия от времени .

Третий участок кривой характеризуется увеличением интенсивности отказов. На этом интервале времени наблюдаются как внезапные, так и постепенные отказы, связанные с износом (старением) элементов. При износе происходит частичное разрушение материалов, изменение их физико-химических свойств. Период износа завершается в точке , когда интенсивность отказов изделия приблизится к максимально допустимой для данного изделия.

При расчетах изделий на надежность с учетом внезапных отказов обычно принимают интенсивность отказов изделий, равную , т.е. расчет производят для нормального участка эксплуатации изделий.

Средние значения номинальной интенсивности отказов для элементов приведены в таблице 1. Эти значения даны для нормальных лабораторных условий эксплуатации изделий (температура – , относительная влажность – 60%, атмосферное давление – 1013 гПа). В реальных условиях эксплуатации внешние воздействия на ЭА могут существенно отличаться от нормальных. Изменение действующих реальных интенсивностей отказов элементов учитывается путем введения поправочных коэффициентов.

При ориентировочных оценках надежности особенности эксплуатации ЭА учитываются следующим образом

, где

– поправочный коэффициент.

всегда больше единицы. Коэффициент учитывает воздействия на ЭА механических факторов (вибраций, ударных нагрузок), – климатических (температуры, влажности), – условия работы при пониженном атмосферном давлении. Значения этих коэффициентов для полупроводниковой ЭА приведены в таблицах 2, 3, 4 соответственно.

При окончательном расчете надежности ЭА расчетные интенсивности отказов элементов уточняются с поправкой на электрические режимы элементов и определяются выражением

, где

– поправочный коэффициент, учитывающий температуру окружающей среды и коэффициент электрической нагрузки . Значения для различных типов элементов приведены в таблице 5. Величина для и температуре окружающей среды близкой к нормальной может быть осуществлено ниже единицы.

Коэффициент нагрузки элемента равен

, где

Н и Н_д – соответственно электрическая нагрузка в реальном и допустимом номинальном (по техническим условиям) режимах. Коэффициент нагрузки либо расчитывается, либо определяется экспериментально, путем замера режимов работы для реальной ЭА.

Коэффициенты нагрузок для различных элементов ЭА находятся следующим образом.

Резисторы

, где

– реальная мощность, рассеиваемая резистором, – допустимая рассеиваемая резистором мощность по справочнику.

Конденсаторы

, где

– реальное напряжение на конденсаторе, – допустимое напряжение на конденсаторе по справочнику.

Полупроводниковые диоды

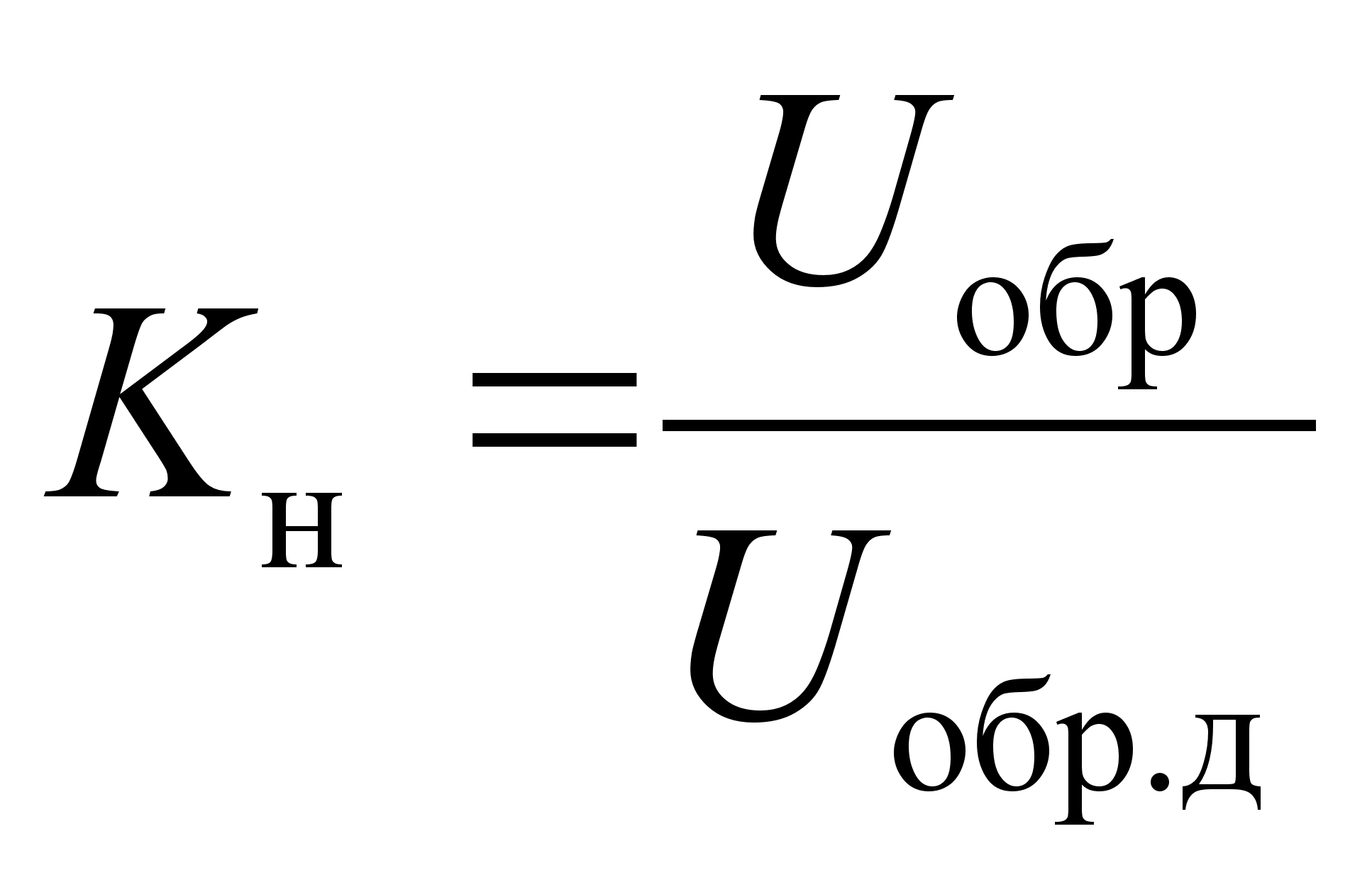, , где

– средний рабочий выпрямленный ток, – выпрямленный допустимый ток, – обратное рабочее напряжение, – допустимое обратное напряжение.

Транзисторы

, , , , , , где

, – токи коллектора и эмиттера; , – допустимые токи коллектора и эмиттера; , , – напряжение коллектор-база, коллектор-эмиттер, эмиттер-база; , , – допустимые напряжения; – мощность, рассеиваемая транзистором; – допустимая мощность.

При определении надежности простой системы обычно вводятся следубщие ограничения.

Отказы, происходящие в системе, являются независимыми.

Отказы системы вызваны отказом элементов. При отказе любого из элементов происходит отказ системы.

Данные ограничения надежности систем без резервирования при расчетах устанавливают математическую модель, состоящую из последовательно включенных элементов (рис.6), независимо от действительных связей элементов в реальной системе.

Рис.6 Последовательная модель системы при расчетах на надежность

Если известны вероятности безотказной работы элементов , то вероятность безотказной работы всей системы равна

.

Полагая в соответствии с выражением (3.4), что и – интенсивность отказа элемента, имеем

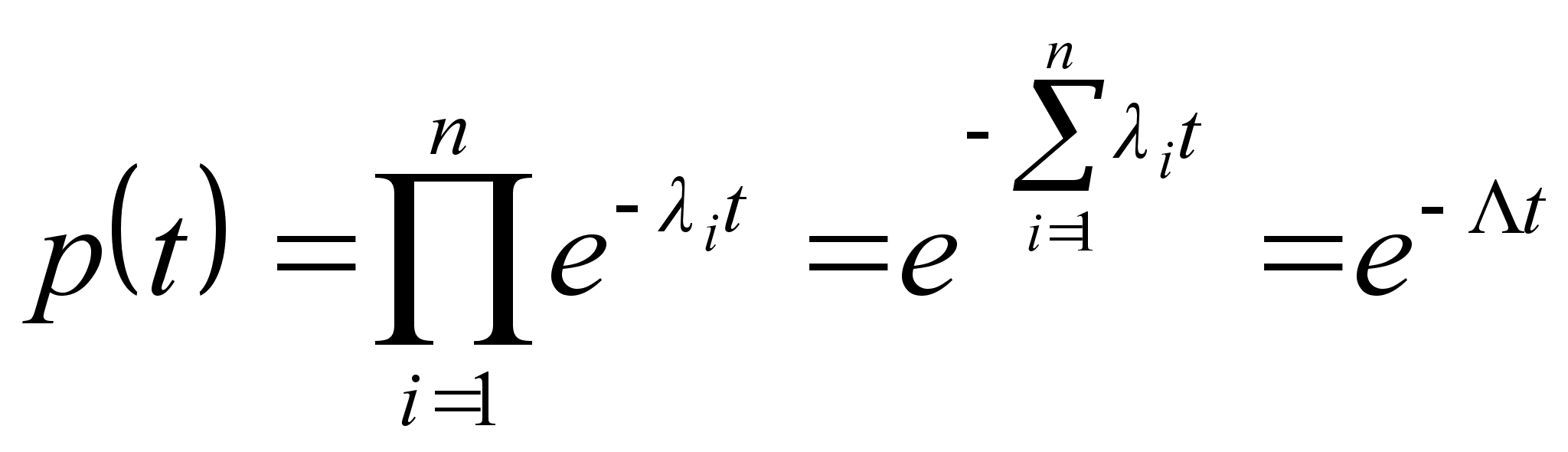, где

– (3.8)

суммарная интенсивность отказов, есть интенсивность отказов системы.

Аналогично выражению (3.6) определяется среднее время безотказной работы системы

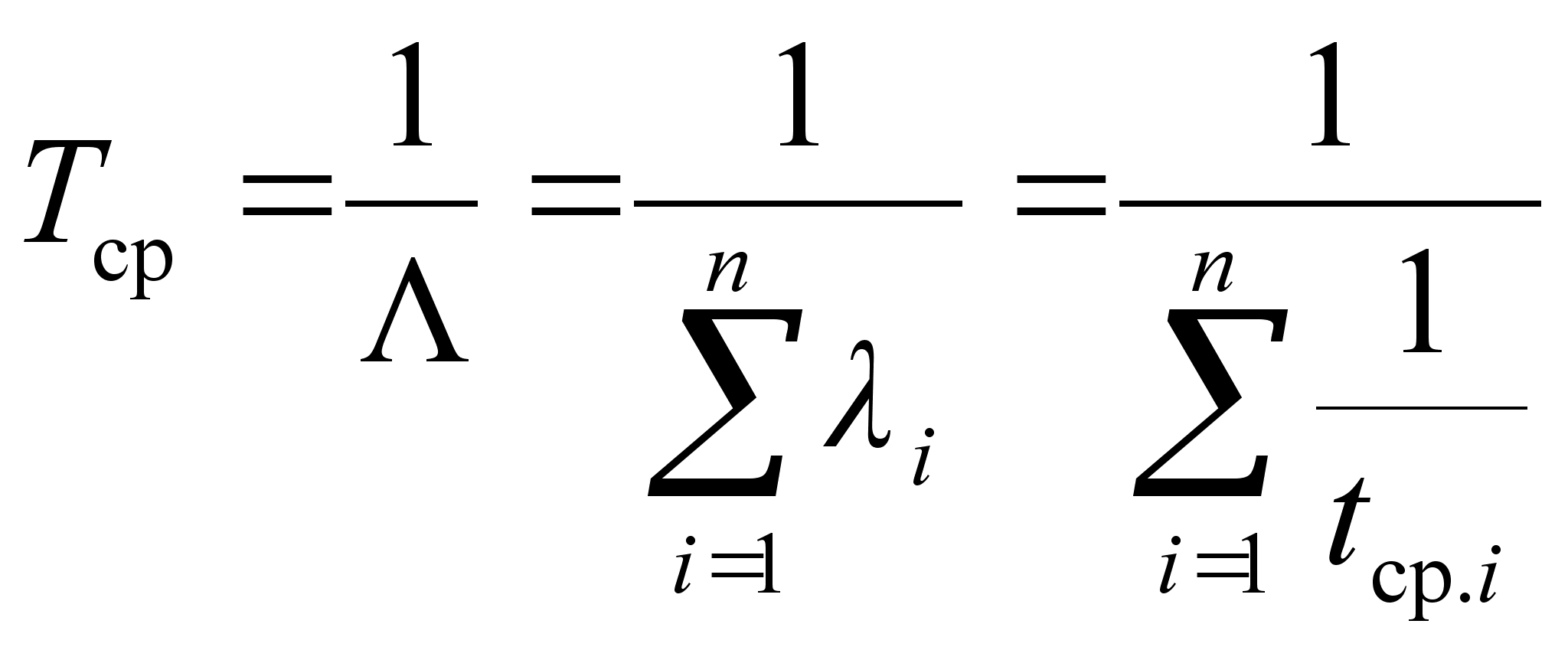. (3.9)

Из приведенных соотношений (3.7) – (3.9) следует:

Чем меньше интенсивность отказов элементов системы, тем выше характеристики надежности самой системы;

Чем меньше общее количество элементов системы, тем лучше характеристики надежности системы.

Таким образом, при конструировании систем необходимо стремиться к более простым системам, состоящим из высоконадежных элементов при заданных ограничениях на технические характеристики и стоимость системы.