Навигация
100 q = 1
t = t + q
s = v * t * COS(f)
h = v * t * SIN(f) - (g * t ^ 2) / 2
PRINT t, h, s
IF h < 0 THEN 200
GOTO 100
200 END
Где V-начальная скорость (м/с), g-ускорение свободного падения (м/с2 ), a-угол, f-формула пересчета угла в радианы, q-единица времени ∆t, t-текущее время, s- проекция горизонтальной дальности, h- высота. Каждой строчке в программе может быть присвоен номер или имя. Причем номера идут по возрастающей, при этом нет необходимости все строчки нумеровать. В данном случае между номером 100 и 200 заложено тело цикла в семь строк. Запуск программы осуществляется RUNSTART.
Программа выдаст решение задачи из трех столбиков значений: t, h, s (табл.2).
Табл.2
| t | H | s |
| 1 | 20.08851 | 43.3079 |
| 2 | 30.37701 | 86.61581 |
| 3 | 30.86552 | 129.9237 |
| 4 | 21.55403 | 173.2316 |
| 5 | 2.442531 | 216.5395 |
| 6 | -26.46896 | 259.8474 |
Из анализа полученных данных делаем вывод, что максимальная дальность падения тела лежит в пределах 216-259 м, а максимальная высота полета превысила 30 м. Более точные значения можно получить уменьшив дискретную составляющую времени ∆t. Если в программе переменной q присвоить 0.5; 0.25; 0.1 и т.д., полученные значения будут более точные. Но полученный объем данных становится не наглядным. Для решения данной задачи, значительно удобней, если решение будет представлено графически.
2. Этап второй. Графика.Сохраним отработанную программу (FILESAVE AS*.bas).
Для построения графика нам потребуется соединить на плоскости уже имеющиеся шесть точек.
Откроем новую программу (FILENEW) и наберем следующий блок:
REM полет тела
REM построение координат
SCREEN 9:
x0 = 50
y0 = 300
x1 = 600
y1 = 100
REM координата Y
LINE (x0, y0)-(x0, y1), 12
LOCATE 18, 4: PRINT "10"
LOCATE 14, 4: PRINT "20"
LOCATE 10, 4: PRINT "30"
LINE (48, 245)-(52, 245), 11
LINE (48, 190)-(52, 190), 11
LINE (48, 135)-(52, 135), 11
REM координата X
LINE (x0, y0)-(x1, y0), 12
LOCATE 23, 19: PRINT "50"
LOCATE 23, 31: PRINT "100"
LOCATE 23, 44: PRINT "150"
LOCATE 23, 56: PRINT "200"
LOCATE 23, 69: PRINT "250"
LINE (150, 302)-(150, 298), 11
LINE (250, 302)-(250, 298), 11
LINE (350, 302)-(350, 298), 11
LINE (450, 302)-(450, 298), 11
LINE (550, 302)-(550, 298), 11
END
Ключевое слово (оператор) SCREEN 9 – обеспечивает перевод в графический режим работы программы. Для построения координат надо учитывать, что точка с координатами X=0, Y=0 лежит в верхнем левом углу экрана монитора. По-этому координаты X0, Y0 определяют начало координат, а X1, Y1- конец координат. Построение линии осуществляется оператором LINE- с указанием координат начала и конца линии и ее цвета (от 0 до 15). Строчка c ключевым словом LOCATE- означает расположить надпись в точке с указанными координатами. После запуска программы на экране появится сетка координат.
Объединим ( EDITCOPY, EDITPASTE) имеющийся блок с сохраненной программой, не значительно ее видоизменив.
REM полет тела
REM построение координат
SCREEN 9:
x0 = 50
y0 = 300
x1 = 600
y1 = 100
x2 = 50
y2 = 300
REM координата Y
LINE (x0, y0)-(x0, y1), 12
LOCATE 18, 4: PRINT "10"
LOCATE 14, 4: PRINT "20"
LOCATE 10, 4: PRINT "30"
LINE (48, 245)-(52, 245), 11
LINE (48, 190)-(52, 190), 11
LINE (48, 135)-(52, 135), 11
REM координата X
LINE (x0, y0)-(x1, y0), 12
LOCATE 23, 19: PRINT "50"
LOCATE 23, 31: PRINT "100"
LOCATE 23, 44: PRINT "150"
LOCATE 23, 56: PRINT "200"
LOCATE 23, 69: PRINT "250"
LINE (150, 302)-(150, 298), 11
LINE (250, 302)-(250, 298), 11
LINE (350, 302)-(350, 298), 11
LINE (450, 302)-(450, 298), 11
LINE (550, 302)-(550, 298), 11
REM полет
v = 50
g = 9.8
a = 30
f = a * 3.14 / 180
100 q = 1
t = t + q
s = v * t * COS(f) (2.1)
h = v * t * SIN(f) - (g * t ^ 2) / 2 (2.2)
LINE (x2, y2)-(x0 + s, y0 - h), 14
x2 = x0 + s
y2 = y0 - h
IF h < 0 THEN 200
GOTO 100
200 END
Веденные дополнительные значения X2, Y2 обеспечивают привязку координат к началу системы отчета. Программа выдаст график полета тела, который в данном случае не привязан к масштабу сетки координат. Устранить это неудобство можно в ведя множитель для Y координаты 5.5 (1:5,5), а для координаты X множитель 2 (1:2).
Заменив строчки 2.1 и 2.2 на выражения 2.3 и 2.4
s = v * t * COS(f) * 2 (2.3)
h = (v * t * SIN(f) - (g * t ^ 2) / 2) * 5.5 (2.4)
получим окончательную программу полета тела (Приложение 1). График полета представлен на рисунке 2.
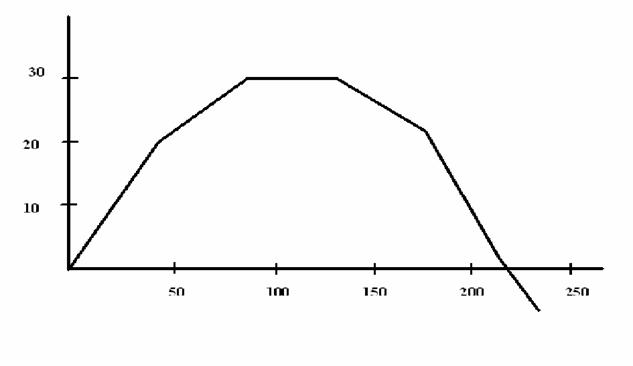
Рис. 2
В данном случаи он не отражает истинной траектории полета тела, так как значение координат получены с шагом (дискретой) в 1 сек. Если значению q присвоить 0,5; 0,25; 0,1; и т.д., то график приблизится к идеальной кривой полета тела.
На кривизну графика так же влияет изменение скорости и начального угла полета тела.
3.Этап третий. Работа пользователя.Хорошую наглядность программа приобретает, когда она становится унифицированной, т.е. чтобы ее можно было успешно использовать для различных параметров. Для того, чтобы можно было менять начальные условия, несколько модернизируем уже имеющуюся программу полета тела. Но вместо тела используем пушечное ядро и попытаемся им попасть в цель находящуюся на каком-то заданном расстоянии.
Для составления программы необходимо учитывать, что начальная скорость ядра составляет примерно 200 м/с, следовательно, и дальность полета значительно возрастет, при этом сопротивлением воздуха опять пренебрегаем. Программу начнем с ввода данных в соответствии с условием задачи.
REM ЯДРО
5 INPUT « Ввести угол стрельбы от 5 до 80 град»; a
7 IF a < 5 THEN 10
IF a > 80 THEN 20
GOTO 40
10 INPUT « Угол должен быть >=5»; a
GOTO 7
20 INPUT « Угол должен быть <=80»; a
GOTO 7
40 INPUT « Ввести дальность до цели от 200 до 5000 м»; l
45 IF l < 200 THEN 50
IF l > 5000 THEN 60
GOTO 70
50 INPUT « Расстояние до цели должно быть >=200»; l
GOTO 45
60 INPUT « Расстояние до цели должно быть <=5000»; l
GOTO 45
70 INPUT « Для выстрела нажать F1»; enter
PRINT a, l
END
Данный отрезок программы, используя условные операторы (IF, THEN), позволяет присвоить переменным a(угол) и l(расстояние), необходимые значения, жестко ограниченные по условию задачи.
Допишем программу с 70-й строки используя за основу программу полета тела, изменив масштаб координат и определив место цели на координате Х:
Похожие работы
... тенденция к снижению снаряда, то таймер 1 останавливается: If Label17.Caption < 150 Then Timer1.Interval = 0 Цель поражена (Рис.13). Рис.13 Заключение Таким образом, язык программирования Visual Basic, наглядно позволяет смоделировать физический процесс, получить конкретные результаты и навыки. Отличительной особенностью VB, является возможность работы его непосредственно в среде Windows, что ...
... Show UserForm14. Hide Следовательно, при ответе «Да» на данный вопрос балл засчитывается в нейротизм. Таким образом, я научилась работать в среде Visual Basic и создавать тестовую программу. Corel DRAW. Введение Corel DRAW является единственным графическим пакетом, позволяющим делать буквально все, начиная от рисования и заканчивая версткой и обработкой растровых изображений[4]. Отличие ...
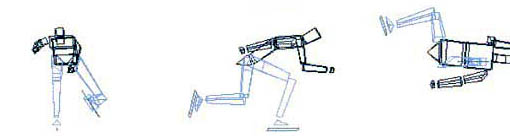
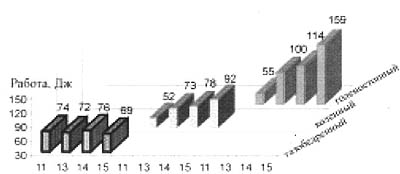
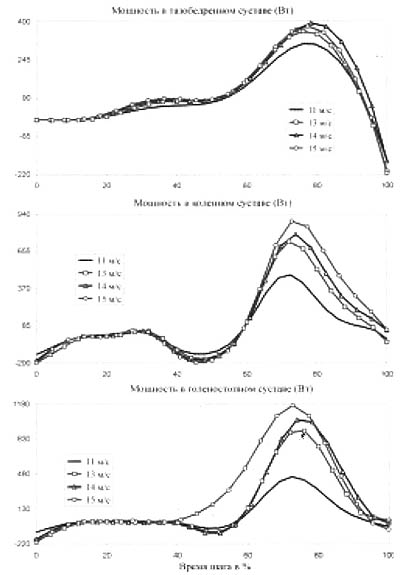
... влияет на конечный результат. Такая постановка имитационной задачи сводится к ответу на вопрос: "Что, если?". Имитационное моделирование в биомеханике . Метод имитационного моделирования применительно к биомеханическим задачам позволяет, не регистрируя кинематику и динамику двигательного действия, только по кинетограмме, созданной на компьютере: а) оценить [6, 41] максимальные усилия мышц; ...
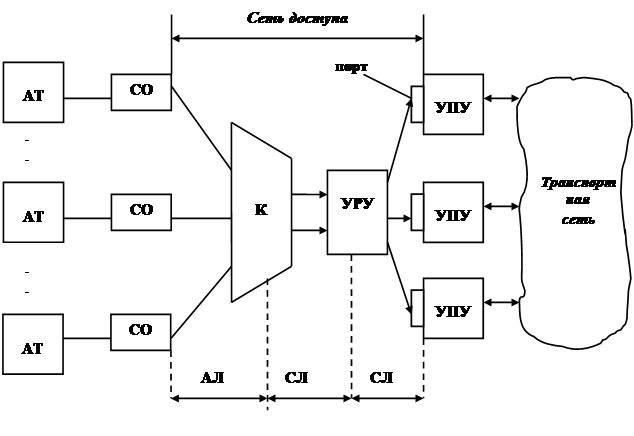
... своевременное распределение средств на развитие. Данными вопросами я и занимаюсь в настоящей дипломной работе. 4. Математическое моделирование Интернет - услуг 4.1 Математическое моделирование dial-up подключений Сначала рассмотрим моделирование услуги предоставления доступа в Интернет по dial-up, так как данная услуга является показателем потенциальных абонентов для монопольной услуги ...


0 комментариев