Навигация
Сравнение с преобразованиями Лоренца
3. Сравнение с преобразованиями Лоренца
Выражение (11) представляет собой упрощенный вариант релятивистских преобразований координат, справедливый при нулевых их начальных значениях (для большей наглядности). Нетрудно видеть, что любые соотношения однонаправленных координат и времен
![]() , (12)
, (12)
представляет собой инвариантную величину, равную скорости света ![]() , что и наблюдается в реальной природе.
, что и наблюдается в реальной природе.
А теперь вновь обратимся к выражению (6). Очевидно, что оно остается справедливым только для одного единственного случая, а именно для плоскости ![]() , проходящей через центр движущейся системы отсчета
, проходящей через центр движущейся системы отсчета ![]() и перпендикулярной вектору скорости ее движения относительно неподвижной системы отсчета.
и перпендикулярной вектору скорости ее движения относительно неподвижной системы отсчета.
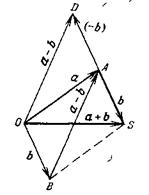
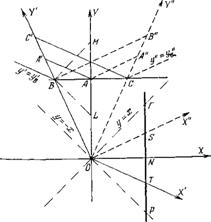
Действительно, если рассмотреть прямоугольный треугольник ![]() (рис. 1) с отрезком
(рис. 1) с отрезком ![]() , лежащим в вышеуказанной плоскости, то видно, что только для него последнее слагаемое в выражении (5) обращается в нуль так, что оно превращается в выражение (6). Таким образом, оказывается, что как ковариантность интервала, так и правомочность использования преобразований Лоренца справедливы только для ортогональных компонент преобразуемых величин (традиционная электродинамика этому удовлетворяет).
, лежащим в вышеуказанной плоскости, то видно, что только для него последнее слагаемое в выражении (5) обращается в нуль так, что оно превращается в выражение (6). Таким образом, оказывается, что как ковариантность интервала, так и правомочность использования преобразований Лоренца справедливы только для ортогональных компонент преобразуемых величин (традиционная электродинамика этому удовлетворяет).
А теперь детальнее проанализируем формулы преобразования Лоренца:
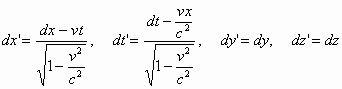 . (13)
. (13)
В них не все так просто, как кажется на первый взгляд. И касается это, в первую очередь, соотношения между интервалом времени между двумя какими-то событиями и величиной единицы времени. Очевидно, что, увеличивая единицу времени (при каких-либо преобразованиях координат), мы тем самым сокращаем интервал времени между двумя событиями. И наоборот, сокращая единицу времени, мы тем самым увеличиваем интервал времени. Так что же описывают преобразования (13): изменение интервала времени или единицы времени?
Если во втором соотношении выражения (13) взять ![]() , то получится выражение
, то получится выражение
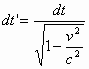 , (14)
, (14)
которое совпадает с формулами преобразований (11) для ![]() и
и ![]() , т.е. “работает” только в плоскости, перпендикулярной вектору скорости движения подвижной системы отсчета.
, т.е. “работает” только в плоскости, перпендикулярной вектору скорости движения подвижной системы отсчета.
Именно так и нужно записывать выражение для изменения единицы времени при переходе к движущейся системе отсчета. Но если преобразуется интервал времени, то соотношение (14) изменится к виду
![]() . (15)
. (15)
Именно данная формула, как считается в СТО, описывает замедление хода времени в движущейся системе отсчета. Однако если наблюдатель находится в движущейся системе отсчета, то все эти рассуждения носят абсолютно противоположный характер, что является полным абсурдом СТО.
В конечном итоге, если перейти к соответствующим соотношениям единиц (дифференциалов) пространства и времени, то данные преобразования нужно записать в виде:
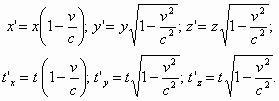 (16)
(16)
Как известно, электромагнитные волны в электродинамике Максвелла поперечны, т.е. их векторы электрической ![]() и магнитной
и магнитной ![]() напряженностей находятся в перпендикулярной к направлению распространения плоскости. Применение преобразований Лоренца к этим компонентам электромагнитного поля давало единственный правильный результат, что и стало триумфом вышеуказанных преобразований. Это подтолкнуло ученых считать и все остальные комбинации правильными.
напряженностей находятся в перпендикулярной к направлению распространения плоскости. Применение преобразований Лоренца к этим компонентам электромагнитного поля давало единственный правильный результат, что и стало триумфом вышеуказанных преобразований. Это подтолкнуло ученых считать и все остальные комбинации правильными.
Между тем, ряд электромагнитных явлений (продольные электромагнитные волны, продольные силы между токовыми элементами, несоблюдение законов сохранения в некоторых задачах традиционной электродинамике и т.п.) уже давно ставят под сомнение всеобщую правильность преобразований Лоренца и полноту уравнений Максвелла. Несоответствие этих преобразований элементарным определениям единиц длины и времени – новое тому доказательство.
Из вышеуказанных рассуждений также вытекает важный вывод о существовании синхронной деформации пространства-времени при переходе от одной инерциальной системы отсчета к другой, а не замедления времени, как это принято в СТО. Данное обстоятельство подтверждается также тем, что вышеуказанные преобразования (11) и (16) не только сохраняют инвариантной скорость света, но и дают правильные результаты для аберрации света и поперечного эффекта Допплера. В то же время продольный эффект Допплера для света должен выражаться такой же формулой, как и соответствующий эффект Допплера для звука при неподвижном относительно воздуха источнике. Это результат различий двух преобразований, касающийся только продольных компонент преобразуемых величин.
Похожие работы
... то поймем, как оно устроено, или, грубо говоря, каковы его основные «исходные компоненты». Тогда станет видно, как эти «компоненты» могут сочетаться в иных комбинациях, образуя иные типы пространств. 2.1 Основные понятия описания пространства-времени 2.1.1 Геометрические векторы и линейные операции над ними Для математического описания пространства удобно пользоваться векторами. Этот объект ...
... позитивистских, а позже – прагматических настроений [14], [15], связанных с отходом от материалистического миропонимания. Поэтому не удивительно, что идея Эйнштейна о необходимости распространения преобразования Лоренца на все без исключения явления материального мира (требование от уравнений физики обязательной лоренц-ковариантной формы) было принято некритически большинством ученых. А было ли ...
... инерциальных системах отсчета. Пространственно-временной континуум – неразрывная связь пространства и времени и их зависимость от системы отсчета. Тема 11. Основные концепции химии 1. Химия как наука, ее предмет и проблемы Важнейшим разделом современного естествознания является химия. Она играет большую роль в решении наиболее актуальных и перспективных проблем современного общества. К ...
... логический смысл безразмерной постоянной тонкой структуры выражается в том, что она показывает соответствие между континуумом Минковского и квартернионным время-пространством. Я полагаю, что Вольфганг Паули, который настаивал на теоретическом обосновании физического статуса этого загадочного числа 137,0306..., имел в виду нечто подобное. Однако формальных аргументов здесь не достаточно. Мы должны ...


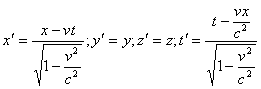

0 комментариев