Математические уравнения модели

4. Математические уравнения модели

Условие максимальности функционала (8) в любом интервале (t1, t2) позволяет применить к нему известное в вариационном исчислении уравнение Эйлера и найти явную зависимость между функциями q(t) и n(t). Но прежде заметим, что, ввиду замкнутости цивилизации, параметр n в любой момент времени должен полностью определяться своими главными внутренними материальными причинами, то есть значением параметра q. Значит, должна существовать функциональная зависимость n = n(q).

Считая это аксиоматическое условие выполненным и применяя к функционалу (8) вариационное уравнение Эйлера [3], приходим к равенству

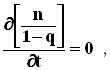
выражающему условие его максимума в любом интервале времени (t1, t2).

Так как моменты t1 и t2 произвольны, то это условие дает:

(9)

Получен первый фундаментальный результат теории - интеграл социального движения:

В периоды медленного и плавного общественного развития удельный относительный фонд потребления c производительной группы остается неизменным. Значит, изменить величину c можно только путем скачкообразного изменения параметров q и n, от которых она зависит.

Из формулы (9) видно, что функция n(q) является линейной, то есть траектории на фазовой плоскости q, n, изображенные на рис.3, являются отрезками прямых линий.

С учётом условия (9), равенство (7) можно записать в виде:

(10)

то есть импульс социальной неустойчивости прямо пропорционален приращению отчуждаемого продукта и обратно пропорционален удельному относительному фонду потребления производительной группы (который постоянен).

Ранее было отмечено, что социальная неустойчивость f может скачком уменьшаться; из (7) следует, что в этом случае уменьшается, также скачком, и величина импульса социальной неустойчивости.

Нетрудно видеть, что локальное уменьшение величин можно осуществить, как это следует из (5), пятью способами:

уменьшить скорость отчуждения , оставив удельный относительный фонд потребления c производительной группы неизменным;

уменьшить и увеличить c;

уменьшить и в меньшей степени уменьшить c;

оставить неизменной величину и увеличить c;

увеличить

и в ещё большей степени увеличить c.

Так как величину c, как это видно из (4), можно изменить, или оставить неизменной, каждый раз тремя способами, то всего получается 15 вариантов скачкообразного уменьшения социальной неустойчивости. Какой из этих вариантов реализуется на практике, в кризисной ситуации назревания скачка величины f, - зависит от соотношения социальных сил и тенденций общественного развития. Однако в любом случае, повторяем ещё раз, социальная неустойчивость после этих скачков может только уменьшиться. (Иначе теряется сам смысл скачка социальной неустойчивости.)

Заметим, что скачки величины f, связанные с изменением относительного удельного фонда потребления

производительной группы, могут сопровождаться резкими изменениями её относительной численности n в ту или иную сторону. Следствием этого может стать множество неблагоприятных общественных явлений, таких как безработица, нехватка рабочей силы и специалистов, массовые репрессии (массовые заключения людей в концлагеря), и даже массовая гибель людей. Последнее, например, имеет место, когда резкое снижение относительной численности производительной группы происходит путём физического уничтожения населения страны – с помощью войн, террора и даже геноцида.

Самым нежелательным из пяти перечисленных способов снижения социальной неустойчивости является третий способ, когда одновременно, скачком, уменьшаются величины и c, то есть когда одновременно, скачком, снижаются темпы экономического развития страны и ухудшается материальное положение членов производительной группы. Тем не менее, на практике возможен и такой способ снижения социальной неустойчивости, о чём свидетельствуют многочисленные примеры из истории человеческих цивилизаций, на которых мы, однако, останавливаться не будем.

Детальное рассмотрение и анализ всех 15 возможных вариантов уменьшения величины f – весьма обширная тема для специальных будущих исследований. В данной работе такое рассмотрение не проводится, поскольку сделать это просто невозможно.

Для начала процесса отчуждения, то есть для момента появления развитых товарно-денежных отношений, частной собственности и государства, характерно, как это следует из формулы (4), приближённое равенство c = 1. (Если в этой формуле положить n = 1, q = 0.) Однако со временем такой относительный фонд потребления перестал удовлетворять членов производительной группы (в основном - рабов), что стало весьма отрицательно сказываться на производительности их труда и процессе отчуждения. В результате рабовладельческое общество, продолжая развиваться, стало в сильной степени внутренне неустойчивым.

Так как для этого общества f =, то, после достижения некоторой критической скорости отчуждения на восходящей ветви экономического цикла, социальная неустойчивость рабовладельческого общества также достигла критической величины, в результате чего произошло скачкообразное, с исторической точки зрения, уменьшение социальной неустойчивости, то есть произошла феодальная революция, в результате которой: быстро уменьшился отчуждаемый продукт q (рабы приобрели кое-какую собственность и стали крепостными крестьянами); уменьшилась относительная численность производительной группы n, за счёт внутренних и внешних войн и роста городов; увеличилась скорость отчуждения (увеличились темпы экономического развития общества), за счёт повышения производительности труда, обусловленного быстрым развитием науки и техники.

Такова же, в общих чертах, сущность и других социальных революций.

Следует остановиться ещё на одном важном обстоятельстве.

Ранее было показано, что удельный относительный фонд потребления производительной группы в периоды медленной эволюции общества постоянен. Но это совершенно не означает постоянства материального положения её членов в абсолютном смысле, так как оно зависит от очень многих факторов, и подвержено значительным не детерминируемым колебаниям. Однако, в длительной перспективе, по мере роста параметра q, то есть экономической развитости общества, удельный относительный фонд потребления производительной группы наполняется всё новым реальным содержанием, так что социальное и материальное положение членов производительной группы (как и остальных людей общества!), в общем, неизменно улучшается. С этой точки зрения, марксистский тезис об абсолютном обнищании пролетариата и людей труда при капитализме является несостоятельным, но невозможность увеличения удельного относительного фонда потребления производительной группы, без социальной революции, К. Марксом угадана правильно.

Несмотря на это положительное обстоятельство, экономические возможности, которыми располагает общество для удовлетворения материальных потребностей производительной группы, всё равно остаются ниже этих потребностей, и это основное социальное противоречие, до окончания процесса отчуждения, нельзя устранить никакими способами.

Формула (9) дает простую линейную зависимость

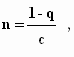(11)

но следует ещё знать зависимость от времени q = q (t).

Для отыскания функции q (t) введем ещё одно очень важное вспомогательное понятие: поле социальных противоречий, характеризуемое функцией двух переменных P(t,n). Но прежде чем определить это понятие математически, заметим следующее.

Процесс отчуждения – это реальный диалектический социальный процесс, характеризуемый двумя безразмерными параметрами q и n. Параметр q характеризует внешнюю сторону этого процесса, то есть ту часть общества, которая не принимает непосредственного участия в производстве материальных благ, но, тем не менее, отчуждает часть из них от производительной группы в свою пользу в силу общественной необходимости. (Не случайно Гегель всегда повторял, что миром движет необходимость.)

Параметр же n характеризует внутреннюю сторону процесса отчуждения, то есть ту часть общества, которая непосредственно производит все материальные блага, в том числе и отчуждаемый продукт q, путём разрешения своих внутренних противоречий, приводящих, в конечном счете, к сокращению относительной численности производительной группы, что, в свою очередь, автоматически ведёт к увеличению относительной численности непроизводительной части общества и к дальнейшему увеличению отчуждаемого продукта. (А на восходящей ветви экономического цикла – ещё и к увеличению скорости отчуждения!).

В результате всего этого получается замкнутая причинно-следственная связь, одновременно порождающая, разрешающая и воспроизводящая социальные противоречия, для количественной оценки которых в данной работе и вводится совершенно новое понятие поля социальных противоречий.

Социальные противоречия как бы пронизывают всю сферу общественного сознания в виде некоторого идеального поля, связывая его неразрывными духовными узами в единую систему и наполняя своим идеальным содержанием все общественные процессы и явления, в том числе и процесс отчуждения.

Поле социальных противоречий – это особая идеальная форма высокоорганизованной материи, необходимая для реализации связей между людьми и функциональными группами. Однако в отличие от материальных полей, идеальное поле социальных противоречий существует только в общественном сознании и в головах и людей. Никакими физическими опытами и приборами его уловить, зафиксировать и измерить невозможно, хотя числовая мера этому полю в данной работе даётся. Здесь кроется кажущийся парадокс материалистической диалектики, которого в жизни на самом деле нет.

В определённом смысле, поле социальных противоречий играет в данной социологической теории такую же роль, как гравитационное поле в небесной механике, электромагнитное поле в электродинамике и кривизна пространства - времени в общей теории относительности Эйнштейна, то есть в его теории гравитации.

После этих предварительных, слегка расплывчатых, но очень важных теоретических рассуждений дадим точное математическое определение идеального поля социальных противоречий, опираясь на материалистическое понимание основного вопроса философии.

Используя принцип вторичности общественного сознания по отношению к общественному бытию, поле социальных противоречий, и сами социальные противоречия, в количественном отношении будем характеризовать некоторой функцией двух переменных P(t, n). Реальные же свойства этой функции, оказывающие воздействия на основные социальные процессы через сознательную деятельность людей, определим следующим образом:

(12)

(13)

где - малый элемент производительной группы; - приращение отчуждаемого продукта, соответствующее малому приращению времени ; t – безразмерное время.

Равенство (12) отражает связь функции социальных противоречий с внешней стороной процесса отчуждения и состоит в том, что дополнительный отчуждаемый продукт , создаваемый в малую единицу времени некоторым малым элементом производительной группы, обусловлен непрерывным ростом функции социальных противоречий (или просто: социальных противоречий) вдоль временной оси, и прямо пропорционален скорости возрастания этой функции и абсолютной величине элемента производительной группы. При этом все элементы считаются однородными, то есть воздействию поля социальных противоречий они подвергаются одинаково. В этом состоит интегрирующая роль этого поля.

Равенство (13) отражает связь поля социальных противоречий с внутренней стороной (неуравновешенностью) процесса отчуждения. Состоит оно в том, что локальный импульс социальной неустойчивости, вычисленный для фиксированного момента времени t, численно равен разности значений функции поля социальных противоречий, взятых при этом значении времени и при значениях второго аргумента, равных и , соответственно.

Заметим, что в интервалах времени, где q=const, n=const, , f=0, функция P(t, n) постоянна. (Социальные противоречия не растут.) В дальнейшем эти интервалы времени из рассмотрения исключаем.

Так как , то уравнение (13) показывает, что вдоль оси (как и вдоль временной оси) функция P(t,n) только растет, поэтому рост социальных противоречий вдоль временной оси можно компенсировать только за счёт одновременного уменьшения относительной численности производительной группы, что и происходит на самом деле.

Используя равенство (10), запишем равенство (13) следующим образом:

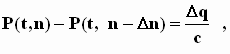
откуда, с учётом обычного осреднённого предельного равенства

получаем совершенно понятное и прозрачное равенство

Далее рассуждаем следующим образом.

Совокупный отчуждаемый продукт q1, создаваемый производительной группой в интервале (t1, t2), и при одновременном уменьшении её численности в этом интервале от n1 до n2 (n1 > n2), равен:

(14)

С другой стороны, равенство (12) позволяет подсчитать величину дополнительного продукта q2, отчуждаемого от производительной группы за время t1 - t2, по-другому, а именно:

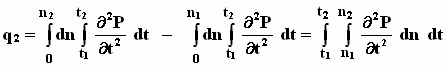(15)

Очевидно, что для любого интервала времени (t1, t2), внутри которого частные производные и непрерывны, выполняется условие неразрывности: q1 = q2, поэтому, сравнивая подынтегральные выражения в интегралах (14) и (15), получаем очень важную дифференциальную зависимость

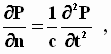(16)

представляющую собой дифференциальное уравнение в частных производных 2-го порядка, решением которого и является функция поля социальных противоречий.

Уравнение (16) – это хорошо известное в математической физике дифференциальное уравнение в частных производных 2-го порядка, описывающее одномерный процесс мгновенного распределения тепла от внезапно возникшего импульсного источника.

Роль линейной координаты в этом уравнении играет безразмерное время t, роль времени – относительная численность производительной группы n, роль температуры – функция поля социальных противоречий P(t,n), роль удельной теплоёмкости – величина , а плотность и коэффициент внутренней теплопроводности “вещества” одномерного стержня (в данном случае - временной оси) равны 1. Вот такая сверхинтересная и сверхудивительная аналогия получается!

Рассмотрим теперь какой-либо непрерывный и гладкий кусок кривой .

Если предположить, что процесс отчуждения завершится в некоторый, заранее неизвестный, момент времени , при заданном значении величины , то задача отыскания функции P(t, n) сводится к следующей:

Найти функцию , удовлетворяющую уравнению (16) и условию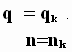

Это модифицированная задача Коши для мгновенного точечного источника, решением которой является фундаментальное решение уравнения теплопроводности, но с одним отличием, что тепло распространяется от импульсного источника тепла (точки с координатой ) не в обе стороны теплопроводного стержня (в данном случае временной оси), а только влево от него.

С учётом этого замечания, нетрудно получить способом, изложенном в [4], следующее фундаментальное решение этой задачи:

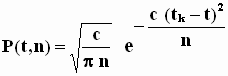(17)

Графики этого довольно простого решения, при фиксированном значении , как функции от t, для отдельных значений параметра n, имеют вид:

Учитывая соотношение (11), запишем уравнение (17) в виде

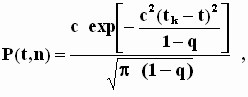 (18)

где .

Отсюда видно, что при фиксированном t, по мере роста отчуждаемого продукта q, функция P(t, n), то есть величина социальных противоречий, уменьшается, так как экспонента, стоящая в знаменателе этой дроби, уменьшается гораздо быстрее, чем уменьшается знаменатель

Для отчуждаемого продукта, с помощью равенств (10) и (13), получаем интегральное уравнение

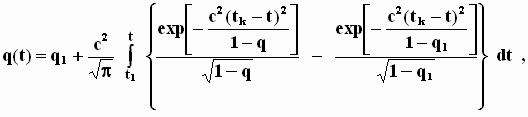
равносильное дифференциальному нелинейному уравнению 1-го порядка

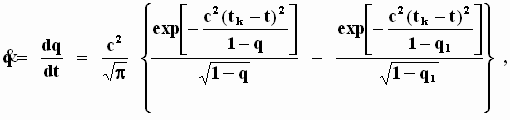
(19)

где - начальный момент времени, а q1 = q(t1).

Поскольку момент времени неизвестен, то, чтобы его найти, хотя бы теоретически, следует, кроме величины q1 задать ещё начальную скорость .

Из этого уравнения, путем численных методов, следует сначала найти неизвестную величину , выразив её через величины , q1 , и c, которые можно считать известными; затем можно численно проинтегрировать дифференциальное уравнение (19) и найти приближенную зависимость q(t), а затем, по формуле (11), - найти неизвестную функцию n(t). Таков трудный и долгий путь решения поставленной задачи. Это работа не для одного человека.

Таким образом, в принципе, основная задача данной работы решена, то есть функции q(t) и n(t) найдены.

В заключение кратко остановимся на характере поведения функции поля социальных противоречий.

Из рис.4 видно, что вдоль временной оси эта функция возрастает, следовательно, социальные противоречия при и с течением времени только растут. Однако скорость их роста, по мере приближения к моменту времени , имеет тенденцию к уменьшению, вплоть до нуля.

Что касается скорости отчуждения и связанной с ней равенством (5) социальной неустойчивости f, то эти величины с течением времени, то есть по мере приближения к моменту времени , стремятся, как это следует из (19), к своим предельным минимальным значениям

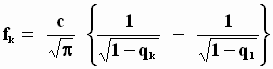
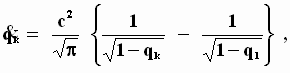
Прибегая к механико-геометрической аналогии, можно сказать, что точка, описывающая траекторию некоторой цивилизации на поверхности функции поля социальных противоречий P(t,n), участвует сразу в двух движениях: поднимается вверх вдоль временной оси и одновременно, чтобы компенсировать социальные противоречия увеличением отчуждаемого продукта, скатывается вбок вниз, вдоль оси параметра q, причём подъем всегда преобладает над спуском.

В конечном счёте, в периоды медленной эволюции общества социальные противоречия только растут, но при этом в любой момент времени возможен, хотя и с разной вероятностью, разрыв функций q(t), , n(t) и P(t, n).

Если же разрыва не произойдёт, то параметры q и n в некоторый момент времени достигнут своих предельных значений qk и nk, при некоторой минимальной, но отличающейся от нуля, скорости отчуждения , и процесс отчуждения на этом закончится. На этом развитие общества, безусловно, не остановится, но предлагаемая физико-математическая модель дальше его не описывает. Можно только предположить, что при товарно-денежные отношения и государство сохранятся, структурная эволюция закончится, а социальные противоречия расти не будут, то есть произойдёт "замораживание" социальных противоречий и одновременно - стагнация его экономического и структурного развития. Этот вывод следует из того, что при можно считать q = const и n = const, как это показано на рис.1, 2. Условно это состояние общества можно считать его концом. Современные интеграционные процессы, имеющие место в Европе, направлены на то, чтобы как можно дольше оттянуть этот конец. Но опять же, это - тема для других, очень трудоёмких, исследований.

Список литературы

1. Г.М. Фихтенголц. “Основы математического анализа”, Т.1, Т.2. М., “Наука”, 1960 г.

2. Ф.Р. Гантмахер. “Лекции по аналитической механике”. М., “Наука”, 1966 г.

3. Л.Э. Эльсгольц. “Дифференциальные уравнения и вариационное исчисление”. М., “Наука”, 1964 г.

4. М.М. Смирнов. “Дифференциальные уравнения в частных производных”. М., “Наука”, 1964 г.

5. К .Маркс. “Капитал”, Т.1. М., “Политиздат”, 1951 г.

6. К. Маркс. “К критике политической экономии”. М., “Политиздат”, 1951 г.

7. “Марксистско-ленинская философия”. Диалектический и исторический материализм. Высшая партийная школа при ЦК КПСС. М., “Мысль”, 1977 г.

8. А.М. Румянцев, Г.А. Козлов и др. “Политическая экономия”, Т.1, Т.2. М., “Политиздат”, 1976 г

Для подготовки данной работы были использованы материалы с сайта http://www.sciteclibrary.ru