Навигация
Схема фильтра с вещественными отводами
3.6.3. Схема фильтра с вещественными отводами
Реализация фильтров по схеме на Рис. 3.10, а сопряжена с некоторыми особенностями, обусловленными комплексным характером коэффициентов в отводах. Поэтому на практике получил распространение еще один вариант схемы такого фильтра, отличающийся вещественным характером коэффициентов.
Фильтр с вещественными коэффициентами получается за счет объединения каждой пары отводов с индексами К и (N-K), которая является комплексно-сопряженной по причине комплексно-сопряженной симметрии частотных характеристик фильтра относительно частоты 0,5wд. В результате
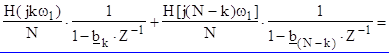
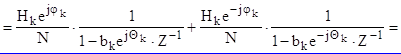
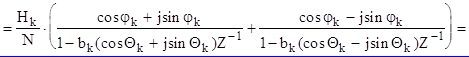
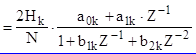 (3.15)
(3.15)
где a0k = cos jk, a1k = -bk cos (jk - qk), b1k = -2bk cos qk, b2k = b2k
Схема вещественного отвода, соответствующего (3.15), приведена на Рис. 3.12.
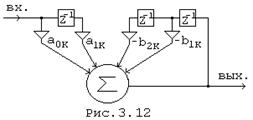
Завершая обсуждение фильтра с частотной выборкой следует отметить еще одно важное качество таких фильтров: в схеме отсутствуют звенья, соответствующие нулевым значениям требуемой АЧХ. В результате, например, схема частотно-селективного фильтра существенно упрощается, сохраняя при этом возможность получения линейной фазы.
3.7. Расчет рекурсивных фильтров. Метод билинейного преобразования.
Методы расчета рекурсивных ЦФ можно разделить на прямые и косвенные. Прямые методы предполагают расчет непосредственно рекурсивного ЦФ, косвенные используют в качестве промежуточного этапа расчет аналогового фильтра (АФ).
К числу косвенных методов относится метод билинейного преобразования, основанный на таком преобразовании частот, при котором частотная ось сжимается до конечных размеров. Формула частотного преобразования
![]() или
или ![]()
где w - реальная частота, т.е. частота проектируемого ЦФ, ![]() - расчетная частота, т.е. частота вспомогательного АФ,
- расчетная частота, т.е. частота вспомогательного АФ, ![]() ,
, ![]() - соответствующие комплексные частоты.
- соответствующие комплексные частоты.
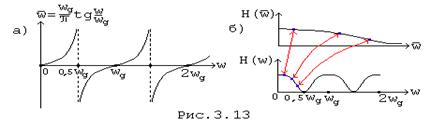
На рис. 3.13, а приведен график зависимости расчетной частоты от реальной частоты, на Рис. 3.13, б - пример соответствия кривых АЧХ фильтров АФ и ЦФ.
Связь комплексных переменных вспомогательного АФ и реального ЦФ, т.е. ![]() и Z определяется равенством
и Z определяется равенством
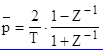 (3.17)
(3.17)
Формула (3.17) получается подстановкой в (3.16) Z = epT. В результате
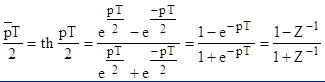
Перечислим последовательность этапов расчета ЦФ методом билинейного преобразования.
1. Перевести требуемые характеристики и нормы ЦФ в соответствующие требования к АФ, применяя формулу
![]()
2. Рассчитать передаточную функцию АФ ![]() , применяя методы расчета аналоговых фильтров.
, применяя методы расчета аналоговых фильтров.
3. Определить передаточную функцию ЦФ H(Z) по известной ![]()
4. Построить схему ЦФ по H(Z).
5. Выполнить необходимые расчеты по учету эффектов конечной разрядности.
Пример. Рассчитать рекурсивный ЦФ нижних частот методом билинейного преобразования по следующим исходным данным:
ПП ® [0; 200] Гц, перех. область ® [200; 300] Гц, DА = 3 дБ, Аmin = 15 дБ.
Решение
Выбираем fд = 800 Гц.
Контрольные частоты для перевода норм ЦФ в нормы АФ: 0; 200 Гц; 300 Гц.
Расчетная формула для преобразования частот
![]()
В результате
f = 0 ® ![]() ® Wн = 0
® Wн = 0
f = 200 Гц ® ![]() 1600 ® Wн = 1
1600 ® Wн = 1
f = 300 Гц ® ![]() 3840 ® Wн = 2,4
3840 ® Wн = 2,4
где Wн = ![]() - нормированная частота ФНЧ,
- нормированная частота ФНЧ,
![]() = 1600 - частота среза ФНЧ.
= 1600 - частота среза ФНЧ.
Основная формула расчета АФ
![]()
В данном случае достаточно ограничиться аппроксимирующим полиномом Баттерворта второго порядка. Поэтому, учитывая что Е=1 для DА = 3 дБ, получаем
![]()
следовательно ![]()
Отсюда полюсы Н(рн): рн 1,2 = -0,707 ± j 0,707,
что соответствует нормированной передаточной функции
![]()
Подставляя здесь
![]() ,
,
получаем денормированную передаточную функцию АФ
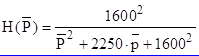
После подстановки здесь (3.17), получаем передаточную функцию рекурсивного ЦФ
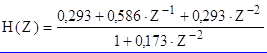
Что соответствует схеме рекурсивного ЦФ, приведенной на Рис. 3.14, а.
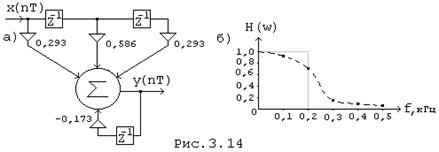
Уместно напомнить, что схему цепи по дробной передаточной функции от Z удобно строить в 2 этапа: вначале строится не рекурсивная часть, соответствующая числителю Н(Z), затем каскадно с ней - рекурсивная часть, соответствующая дроби, в числителе которой - единица.
График реализованной АЧХ приведен на рис. 3.14, б.
Нелинейная зависимость частотного преобразования (3.16) определяет как недостатки, так и достоинства метода билинейного преобразования. Недостаток в том, что наклонные участки частотной характеристики изменяют свой наклон тем больше, чем выше частота. Поэтому, например, линейная фаза после преобразования (3.16) становится нелинейной. Достоинство определяется отсутствием ошибок наложения при переходе АФ ® ЦФ, что позволяет получить высокие уровни ослабления в ПН при конструировании частотно-селективных фильтров.
Похожие работы
... Студент группы 220352 Чернышёв Д. А. Справка— отчет о патентном и научно- техническом исследовании Тема выпускной квалификационной работы: телевизионный приёмник с цифровой обработкой сигналов. Начало поиска 2. 02. 99. Окончание поиска 25.03.99 Предмет поиска Страна, Индекс (МКИ, НКИ) № ...
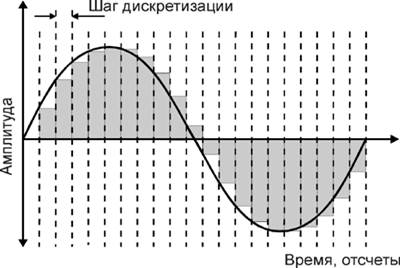
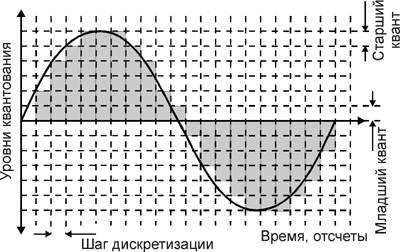
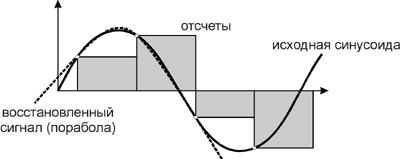
... 1 – «-» Причем 1-ый разряд слева – знаковый разряд. 16 14 12 10 8 6 4 2 Т 2Т 2. Связи между аналоговыми и дискретными сигналами. При обработке сигнала на ЭВМ необходимо в максимальной степени, чтобы дискретный или цифровой сигнал содержал все признаки аналогового сигнала. При дискретизации возможна потеря информации, которая ...
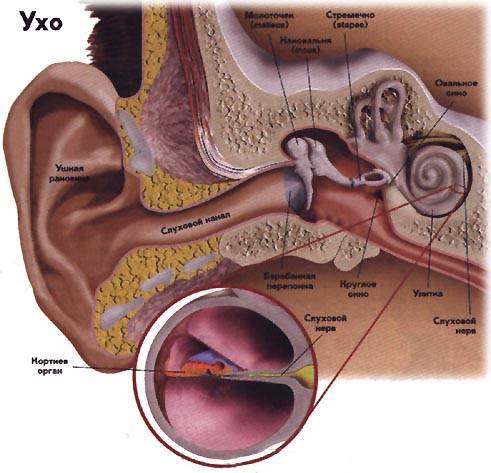
... примерно 6%. В общем, в районе 1 - 4 кГц чувствительность уха по всем параметрам максимальна, и составляет не так уж и много, если брать не логарифмированные значения, с которыми приходится работать цифровой технике. Примите на заметку - многое из того, что происходит в цифровой обработке звука, может выглядеть ужасно в цифрах, и при этом звучать неотличимо от оригинала. В цифровой обработке ...
... несущими и амплитудно-фазовая модуляция с одной боковой полосой (АФМ-ОБП). 3. Выбор длительности и количества элементарных сигналов, используемых для формирования выходного сигнала В реальных каналах связи для передачи сигналов по частотно ограниченному каналу используется сигнал вида , но он бесконечен во времени, поэтому его сглаживают по косинусоидальному закону. , где - ...
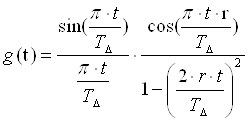
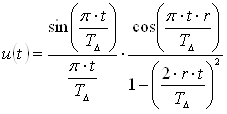
0 комментариев