Валерий Петров
Более 350 лет математики всего мира безуспешно ищут ответ на вопрос: «Верна ли великая теорема Ферма?». Не находит его и дьявол, изучив за 10 часов все без исключения разделы математики и потратив остаток времени на собственные изыскания, он, за 10 минут до истечения срока, появляется с пачкой исписанных листков, швыряет их на пол и топчет ногами. И, признав свое поражение, исчезает... Однако спустя несколько минут появляется вновь и вместе с человеком начинает искать ответ на поставленный вопрос».
В действительности, однако, все было несколько иначе. Когда дьявол узнал об условии заключения договора с ученым-математиком о продажи его души, он рассмеялся и сказал: «Нет ничего проще. У меня есть доказательство этой теоремы, написанное самим Ферма». С этими словами дьявол достал из кармана аккуратно сложенный лист бумаги и протянул его ученому. Флэгг уселся поудобнее в кресло у камина и стал читать.
«Пусть имеется три целых числа, удовлетворяющих уравнению:
| z3 = x3 + y3 | (1) |
Очевидно, эти числа попарно не должны иметь общих множителей. Также очевидно, что число z меньше суммы двух других чисел, т.е.
| z < x + y | (2) |
Пусть имеется три отрезка длиной z, x, y, удовлетворяющих условию (2). Тогда в силу известной теоремы на этих отрезках можно построить треугольник как на сторонах. Предположим, что треугольник прямоугольный. Тогда для сторон этого треугольника справедливы два соотношения:
z3 = x3 + y3 и z2 = x2 + y2,
откуда следует:
![]()
![]()
(x3 + y3)2 = (x2 + y2)3;
x6 + 2x3y3 + y6 = x6 + 3x4y2 + 3x2y4 + y6;
2x3y3 = 3x4y2 + 3x2y4;
2x3y3 = 3x2y2(x2 + y2);
2xy = 3(x2 + y2).
Пусть x = y + b. Тогда:
2y(y + b) = 3(x2 + y2);
2y2 + 2yb = 3x2 + 3y2;
2y2 + 2yb – 3y2 = 3x2;
2yb – y2 = 3x2;
y(2b – y) = 3x2;
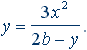
Пусть 2b – y = c, тогда y = 3x2/c.
Пусть 3/c = d, тогда
| y = dx2 | (3) |
Таким образом, число x является одним из сомножителей числа y, что недопустимо и, следовательно, уравнение (1) не имеет целочисленных решений удовлетворяющих условию (2).
Применяя бином Ньютона для возведения в степень суммы чисел x2+y2 в степень, можно аналогичным образом доказать теорему для любых чисел n>3.
Известно, однако, что существует теорема, согласно которой треугольник, между сторонами которого имеется соотношение zn=xn+yn, при n>3 является остроугольным. Тогда для сторон этого треугольника справедливы два соотношения:
zn = xn + yn и z2 = x2 + y2 + 2xy · cosα,
где α – угол между сторонами x и y.
Однако и в этом случае доказательство сводится к тому, что y оказывается равным dx2, так же, как это было показано для прямоугольного треугольника (3).
Флэгг задумался на мгновенье и неожиданно швырнул бумагу прямо в огонь. «Зачем Вы это сделали?» – воскликнул дьявол. «Я нахожу, что слишком дешево продал свою душу. Так пусть же никто больше не воспользуется этим доказательством!» – ответил Флэгг.
«В самом деле», подумал дьявол, «пусть математики еще поломают головы над доказательством этой теоремы».
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.n-t.org/
Похожие работы
... , что возможно, наша цивилизация подойдет к концу прежде, чем удастся доказать Великую теорему Ферма. Доказательство Великой теоремы Ферма стало самым ценным призом в теории чисел, и поэтому не удивительно, что поиски его привели к некоторым наиболее захватывающим эпизодам в истории математики. В эти поиски оказались вовлеченными величайшие умы на нашей планеты, за доказательство назначались ...
... іють властивостями, аналогічними властивостям магічних квадратів. Хоча Ферма вніс великий внесок до розвитку теорії чисел алгебри, докази його доводів майже ні в одному випадку знайдені не були (доведення Великої теореми Ферма для n=4 – виключення, оскільки в рукописах воно було). Деякі виводи, зроблені Ферма, були і зовсім помилковими, але теореми, повні докази яких, як затверджував Ферма, у ...
... n = q ³ 3 и четном значении z также не имеет целочисленных решений. Поэтому далее достаточно доказать, что целочисленных решений не имеет также и уравнение (14). Доказательство великой теоремы ферма. Уравнения (1) и (14) полностью эквивалентны, т.е. либо не существует целочисленных решений у обоих уравнений, либо целочисленные решения одновременно имеют уравнения (1) и (14). Покажем, что ...
... алгебраических чисел. – М. – Наука. – 1982. - С. 13). Вывод: Великая теорема Ферма для степени простом доказана. ******** Утверждение 2, частным случаем которого является Великая теорема Ферма, для показателя q = 4 Часть 1 Уравнение ( - четное, q = 4 = 2m, где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах , и таких, чтобы - было четным, и - ...
0 комментариев