Навигация
3.3 Û 4.3, 3.4 Û 4.4.
Первая их этих эквиваленций означает, что стратегия Ai является оптимальной по критерию 3.3 тогда и только тогда, когда она оптимальна по критерию 4.3.
Аналогичное объяснение относится и ко второй эквиваленции.
Доказательство. Докажем сначала эквиваленцию 3.3 Û 4.3. Так как функции игры W и S соответственно критериев 3.3 и 4.3 удовлетворяют равенству S = –W, то и показатели игры удовлетворяют аналогичному равенству Sij = –Wij. Тогда
![]()
откуда
![]() .
.
Таким образом, Si будет минимальным для номера i, для которого Wi будет максимальным, и эквиваленция 3.3 Û 4.3 доказана.
Совершенно аналогично доказывается и эквиваленция 3.4 Û 4.4. n
Максимаксные критерии (крайнего оптимизма).
В данном случае функция игры, которую мы обозначим через M(a, r, q), должна не убывать по выигрышу ![]() и по вероятности
и по вероятности ![]() состояний природы и не возрастать по риску
состояний природы и не возрастать по риску ![]() :
:
M(a, r, q) Ú а; Ø по r; по Ú q. (8)
Показатели игры Mij= M(aij, rij, qj). Показатели оптимальности стратегий
![]()
Оптимальной называется стратегия Ai0, для которой
![]() .
.
Максимаксные критерии являются критериями крайнего оптимизма, поскольку предполагают, что природа будет находиться в наиболее благоприятном для игрока А состоянии и потому в качестве оптимальной выбирается стратегия, при которой максимальный показатель игры – показатель оптимальности максимален среди максимальных показателей всех стратегий.
В качестве максимаксных критериев с конкретными функциями игры M(a, r, q), обладающими свойствами (8), можно взять, например, следующие:
5.1. M(a, r, q) = а;
5.2. M(a, r, q) = qa;
5.3. M(a, r, q) = a-r;
5.4. M(a, r, q) =qa-(1-q)r.
В критерии 5.1 показателями игры являются выигрыши Mij = aij, и мы получаем максимаксный критерий относительно выигрышей ([2], с. 42).
Миниминные критерии (крайнего оптимизма).
Функция игры, обозначим ее через E(a, r, q), выбирается невозрастающей по выигрышу а и по вероятности q состояний природы и неубывающей по риску r:
E(a, r, q) Ø по а; Ú по r; Ø по q. (9)
В качестве показателей неоптимальности стратегий Аi берутся
![]()
где Eij = E(aij, rij, qi) – показатели игры.
Оптимальной назначается стратегия Ai0, минимизирующая показатель неоптимальности ![]() , т.е.
, т.е.
![]()
Миниминные критерии также являются критериями крайнего оптимизма, поскольку под оптимальной стратегией понимается стратегия, при которой показатель неоптимальности минимален среди показателей неоптимальности всех стратегий.
Примерами миниминных критериев с функциями игры E(a, r, q) со свойствами (9) могут быть:
6.1. E(a, r, q) = r;
6.2. E(a, r, q) = (1–q)r;
6.3. E(a, r, q) = r –a;
6.4. E(a, r, q) = (1–q)r –qa.
Показателями игры в критерии 6.1 являются риски, и он, таким образом, превращается в миниминный критерий относительно рисков.
Утверждение 2. Максимаксные критерии 5.3 и 5.4 эквиваленты соответственно миниминным критерием 6.3 и 6.4:
5.3 Û 6.3, 5.4 Û 6.4.
Доказательство аналогично доказательству утверждения 1, а именно для критериев 5.3 и 6.3 имеем: E = –M и, следовательно, Eij = –Mij, откуда
![]()
Поэтому
![]()
Таким образом, эквиваленция 5.3 Û 6.3 доказана.
Аналогично доказывается и эквиваленция 5.4 Û 6.4. n
Для лучшей обозримости стрелок, указывающих в (4), (5), (8) и (9) на невозрастание или неубывание функций игры рассмотренных критериев в пп. 3, 4, 5, 6 в зависимости от выигрышей а, рисков r и состояний природы q, сведем их в следующую таблицу.
Таблица 1
| Аргументы | Функции игры и критерии | |||
| функций игры | W(a, r, q) | S(a, r, q) | M(a, r, q) | E(a, r, q) |
| max min | min max | max max | min min | |
| a | Ú | Ø | Ú | Ø |
| r | Ø | Ú | Ø | Ú |
| q | Ø | Ú | Ú | Ø |
Из этой таблицы видно, что стоящие в первой строке стрелки, обозначающие поведение функций игры в зависимости от выигрышей а, соответствуют первому значку в названии критерия: max – Ú , min – Ø , ,max – Ú , min – Ø . А стрелки во второй строке, обозначающие поведение функций игры в зависимости от рисков r , противоположны стрелкам первой строки.
Критерии максимизации взвешенного среднего показателя оптимальности стратегий.
Функция игры L(a, r, q) должна неубывать по выигрышу a и невозрастать по риску r :
L(a, r, q) Ú по а; Ø по r. (10)
Показатели оптимальности стратегий Ai0 определяются следующим образом:
![]() (11)
(11)
где Lij = L(aij, rij, qj) – показатели игры.
По определению оптимальной является стратегия Ai0, максимизирующая показатель оптимальности Li:
![]()
В качестве функций игры L(a, r, q), удовлетворяющих условиям (10), можно взять функции:
Похожие работы
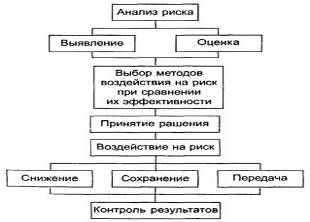
... , способных нанести урон компании. Вместе с тем рисками можно управлять так же, как процессами производства или закупки материалов. Для того чтобы компания могла принимать обоснованные решения в условиях неопределенности, она должна выработать политику по управлению рисками. Управление рисками следует регламентировать специальным внутренним документом – программой по управлению рисками. Основная ...
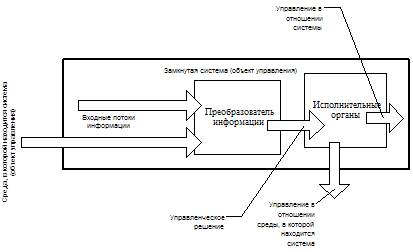
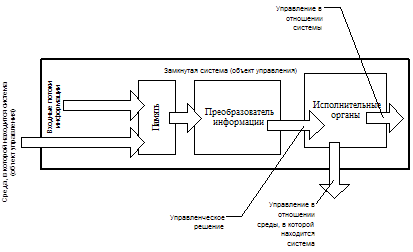
... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...
... . // Информатика и образование. -1994. - №4. 45. Подиновский В.В., Ногин В.Д. Паретооптимальные решения многокритериальных задач. - М.: Наука, 1982, - 256 с., ил. 46. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр: Учебное пособие для университетов: / - М.: Высш. шк., Книжный дом "Университет", 1998. - 304с.: ил. 47. Программа курса информатики для начальной школы по ...
... из сторон преследует собственные цели, не всегда совпадающие друг с другом. Неопределенность такого рода при принятии решений относят к классу поведенческих неопределенностей. Теоретической основой нахождения оптимального решения в условиях неопределенности и конфликтных ситуаций является теория игр. Игра - это математическая модель процесса функционирования конфликтующих элементов систем, в ...



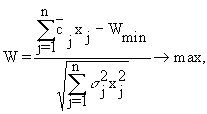
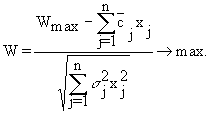
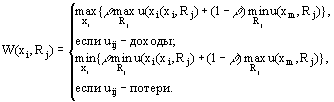
0 комментариев