Навигация
8.1, 7.1 8.2, 7.2 8.1, 7.2 8.2, из которыx следует требуемая экиваленция (13)
7.1 8.1, 7.1 8.2, 7.2 8.1, 7.2 8.2, из которыx следует требуемая экиваленция (13).
Отметим, что эквиваленция 7.1 8.1 – известный факт (доказанный, например, в [1], с. 502).
Из эквиваленции (13) можно сделать вывод о том, что из критериев 7.1, 7.2, 8.1, 8.2 достаточно применить один, причем с более простой функцией игры.
Максиминно-максимаксные критерии.
Такие критерии представляют собой комбинации максиминного и максимаксного критериев. В качестве показателя оптимальности стратегии ![]() берется величина
берется величина
![]()
где [0,1]– коэффициент оптимизма, а ![]() и
и ![]() – показатели оптимальности стратегии Ai соответственно в максиминном и максимаксном критериях (см. п. 3 и п. 5). При этом функции игры в этих двух критериях целесообразно использовать соответствующие друг другу. Это соответствие показано в табл. 3.
– показатели оптимальности стратегии Ai соответственно в максиминном и максимаксном критериях (см. п. 3 и п. 5). При этом функции игры в этих двух критериях целесообразно использовать соответствующие друг другу. Это соответствие показано в табл. 3.
Таблица 3
| Критерии | Выигрыши a | Риски r | Вероятности состояний природы q | W (a, r, q) | M (a, r, q) |
| 9.1 | + | a | a | ||
| 9.2 | + | + | (1-q)a | qa | |
| 9.3 | + | + | a-r | a-r | |
| 9.4 | + | + | + | (1-q)a-qr | qa-(1-q)r |
Оптимальной считается стратегия Ai0, максимизирующая показатель оптимальности Нi( ):
![]()
Коэффициент оптимизма выбирается субъективно в пределах от 0 до 1, включая концы, в зависимости от опасности ситуации: чем более опасной представляется ситуация, тем меньше оптимизма и тем меньше коэффициент оптимизма ; чем более благоприятная ситуация, тем больше оптимизма и значит можно выбирать ближе к 1.
При наименьшем значении коэффициента оптимизма = 0 данный критерий превращается в максиминный критерий крайнего пессимизма, а при наибольшем значении коэффициента оптимизма = 1 рассматриваемый критерий превращается в максимаксный критерий крайнего оптимизма. При = 1/2 максиминно-максимаксный критерий можно считать критерием реализма.
Критерий 9.1 является критерием Гурвица относительно выигрышей ([1], с. 505; [2], с. 120; [3], с. 47; [5], с. 57).
Минимаксно-миниминные критерии.
Минимаксно-миниминные критерии являются результатом комбинации минимаксного и миниминного критериев. Показатель неоптимальности стратегии Ai определяется следующим образом:
![]()
где [0,1]– коэффициент оптимизма, а ![]() и
и ![]() – показатели неоптимальности стратегии Ai соответственно в минимаксном и миниминном критериях (см. п. 4 и п. 6). Функции игры в этих двух критериях лучше выбирать соответствующими друг другу, как это указано в табл. 4.
– показатели неоптимальности стратегии Ai соответственно в минимаксном и миниминном критериях (см. п. 4 и п. 6). Функции игры в этих двух критериях лучше выбирать соответствующими друг другу, как это указано в табл. 4.
Таблица 4
| Критерии | Выигрыши a | Риски r | Вероятности состояний природы q | S (a, r, q) | M (a, r, q) |
| 10.1 | + | r | r | ||
| 10.2 | + | + | qr | (1-q)r | |
| 10.3 | + | + | r-a | r-a | |
| 10.4 | + | + | + | qr-(1-q)a | (1-q)r-qa |
Оптимальной по критерию является стратегия Ai0, для которой
![]() .
.
Данный критерий превращается в минимаксный критерий при = 0, в миниминный критерий при = 1, в критерии Гурвица относительно рисков при ![]() (критерий 10.1).
(критерий 10.1).
Утверждение 4. При одном и том же коэффициенте оптимизма ![]() максиминно-максимаксные критерии 9.3 и 9.4 эквиваленты соответственно минимаксно-миниминным критериям 10.3 и 10.4.
максиминно-максимаксные критерии 9.3 и 9.4 эквиваленты соответственно минимаксно-миниминным критериям 10.3 и 10.4.
Доказательство. Для критериев 10.3 и 9.3 имеем:
![]()
откуда
![]()
т.е. показатель неоптимальности Di( ) будет минимальным для того значения i, для которого показатель оптимальности Hi( ) будет максимален. Таким образом, эквиваленция 9.3 10.3 доказана.
Эквиваленция 9.4 10.4 доказывается аналогично. n
ПРИМЕР. Рассмотрим игру с природой, в которой игрок А имеет возможность применить одну из четырех стратегий А1, А2, А3, А4, а природа П может находиться в одном из трех состояний П1, П2, П3 с вероятностями соответственно q1 = 0,7; q2 = 0,1; q3 = 0,2. Известны выигрыши (aij) игрока А. Найдем оптимальные стратегии по рассмотренным выше критериям.
Выпишем таблицы показателей игры и в дополнительных столбцах – показатели оптимальности и неоптимальности для соответствующих критериев. При этом на основании утверждений 1-4 из эквивалентных критериев будем рассматривать только один.
| Таблица для критериев 3.1 и 5.1 | Таблица для критерия 3.2 | |||||||||||
| Пj Ai | П1 | П2 | П3 | Wi | Mi | Пj Ai | П1 | П2 | П3 | Wi | ||
| A1 | 4 | 7 | 1 | 1 | 7* | A1 | 1,2 | 6,3 | 0,8 | 0,8 | ||
| (aij) = | A2 | 4 | 3 | 5 | 3* | 5 |
| A2 | 1,2 | 2,7 | 4,0 | 1,2 |
| A3 | 6 | 5 | 2 | 2 | 6 | A3 | 1,8 | 4,5 | 1,6 | 1,6* | ||
| A4 | 0 | 6 | 3 | 0 | 6 | A4 | 0,0 | 5,4 | 2,4 | 0,0 |
Таблица для критериев 4.1 и 6.1 Таблица для критерия 4.2
| Пj Ai | П1 | П2 | П3 | Si | Ei | Пj Ai | П1 | П2 | П3 | Si | ||
| A1 | 2 | 0 | 4 | 4 | 0* | A1 | 1,4 | 0,0 | 0,8 | 1,4 | ||
| (rij) = | A2 | 2 | 4 | 0 | 4 | 0* | (qjrij) = | A2 | 1,4 | 0,4 | 0,0 | 1,4 |
| A3 | 0 | 2 | 3 | 3* | 0* | A3 | 0,0 | 0,2 | 0,6 | 0,6* | ||
| A4 | 6 | 1 | 2 | 6 | 1 | A4 | 4,2 | 0,1 | 0,4 | 4,2 |
Таблица для критерия 3.3 и 5.3 Таблица для критерия 3.4
| Пj Ai | П1 | П2 | П3 | Wi | Mi | Пj Ai | П1 | П2 | П3 | Wi | ||
| A1 | 2 | 7 | -3 | -3 | 7* | A1 | -0,2 | 6,3 | 0,0 | -0,2 | ||
| (аij–rij)= | A2 | 2 | -1 | 5 | -1* | 5 | ((1-qj )аij– qjrij)= | A2 | -0,2 | 2,3 | 4,0 | -0,2 |
| A3 | 6 | 3 | -1 | -1* | 6 | A3 | 1,8 | 4,3 | 1,0 | 1,0* | ||
| A4 | -6 | 5 | 1 | -6 | 5 | A4 | -4,2 | 5,3 | 2,0 | -4,2 |
Таблица для критерия 5.2 и 7.1 Таблица для критерия 6.2
| Пj Ai | П1 | П2 | П3 | Mi | Li | Пj Ai | П1 | П2 | П3 | Ei | ||
| A1 | 2,8 | 0,7 | 0,2 | 2,8 | 3,7 | A1 | 0,6 | 0,0 | 3,2 | 0,0* | ||
| (qj аij) = | A2 | 2,8 | 0,3 | 1,0 | 2,8 | 4,1 | ((1-qj)rij) = | A2 | 0,6 | 3,6 | 0,0 | 0,0* |
| A3 | 4,2 | 0,5 | 0,4 | 4,2* | 5,1* | A3 | 0,0 | 1,8 | 2,4 | 0,0* | ||
| A4 | 0,0 | 0,6 | 0,6 | 0,6 | 1,2 | A4 | 1,8 | 0,9 | 1,6 | 0,9 |
Таблица для критерия 5.4
| Пj Ai | П1 | П2 | П3 | Mi | |
| A1 | 2,2 | 0,7 | -3,0 | 2,2 | |
| (qj aij -(1-qj)rij) = | A2 | 2,2 | -3,3 | 1,0 | 2,2 |
| A3 | 4,2 | -1,3 | -2,0 | 4,2* | |
| A4 | -1,8 | -0,3 | -1,0 | -0,3 |
Теперь выпишем таблицы показателей оптимальности для критериев 9 с коэффициентом оптимизма = 1/2.
Таблица для критерия 9.1 Таблица для критерия 9.2
| Ai | Wi =
| Mi =
| Hi(1/2)= | Ai | Wi =
| Mi =
| Hi(1/2)= | |
| A1 | 1 | 7 | 4* | A1 | 0,8 | 2,8 | 1,8 | |
| A2 | 3 | 5 | 4* | A2 | 1,2 | 2,8 | 2,0 | |
| A3 | 2 | 6 | 4* | A3 | 1,6 | 4,2 | 2,9* | |
| A4 | 0 | 6 | 3 | A4 | 0,0 | 0,6 | 0,3 |
Таблица для критерия 9.3 Таблица для критерия 9.4
| Ai | Wi =
| Mi =
| Hi(1/2)= | Ai | Wi =
| Mi =
| Hi(1/2)= | |
| A1 | -3 | 7 | 2 | A1 | -0,2 | 2,2 | 1,0 | |
| A2 | -1 | 5 | 2 | A2 | -0,2 | 2,2 | 1,0 | |
| A3 | -1 | 6 | 2,5* | A3 | 1,0 | 4,2 | 2,6* | |
| A4 | -6 | 5 | -0,5 | A4 | -4,2 | -0,3 | -2,25 |
Выпишем таблицы показателей неоптимальности для критериев 10.
| Таблица для критерия 10.1 | Таблица для критерия 10.2 | |||||||
| Ai | Si=
| Ei=
| Hi(1/2)= | Ai | Si=
| Ei=
| Hi(1/2)= | |
| A1 | 4 | 0 | 2 | A1 | 1,4 | 0,0 | 0,7 | |
| A2 | 4 | 0 | 2 | A2 | 1,4 | 0,0 | 0,7 | |
| A3 | 3 | 0 | 1,5* | A3 | 0,6 | 0,0 | 0,3* | |
| A4 | 6 | 1 | 3,5 | A4 | 4,2 | 0,9 | 2,55 |
Звездочкой * во всех таблицах отмечены оптимальные по соответствующему критерию стратегии.
Для лучшей обозримости сведем полученные результаты в таблицу.
Таблица оптимальных стратегий по различным критериям
| № критерия | Критерии. Функции игры | Оптимальная стратегия |
| 3 | Максиминные критерии (крайнего пессимизма) | |
| 3.1 | W(a,r,q)=a | A2 |
| 3.2 | W(a,r,q)=(1-q)a | A3 |
| 3.3 | W(a,r,q)=a-r | A2 , A3 |
| 3.4 | W(a,r,q)=(1-q)a-qr | A3 |
| 4 | Минимаксные критерии (крайнего пессимизма) | |
| 4.1 | S(a,r,q)=r | A3 |
| 4.2 | S(a,r,q)=qr | A3 |
| 5 | Максимаксные критерии (крайнего оптимизма) | |
| 5.1 | М(a,r,q)=а | А1 |
| 5.2 | М(a,r,q)=qа | А3 |
| 5.3 | М(a,r,q)=а-r | A1 |
| 5.4 | М(a,r,q)=qa-(1-q)r | А3 |
| 6 | Миниминные критерии (крайнего оптимизма) | |
| 6.1 | E(a,r,q)=r | A1, A2, A3 |
| 6.2 | E(a,r,q)=(1-q)r | A1, A2, A3 |
| 7 | Критерий максимизации взвешенного среднего выигрыша (критерий Лапласа) | |
| 7.1 | L(a,r,q)=qа | А3 |
| 9 | Максиминно-максимаксные критерии с коэффициентом оптимизма =1/2 | |
| 9.1 | W(a,r,q)= М(a,r,q)=а | A1, A2, A3 |
| 9.2 | W(a,r,q)=(1-q)a; М (a,r,q)=qа | А3 |
| 9.3 | W(a,r,q)= М(a,r,q)=a-r | А3 |
| 9.4 | W(a,r,q)=(1-q)a-qr; М(a,r,q)=qa-(1-q)r | А3 |
| 10 | Минимаксно-миниминные критерии с коэффициентом оптимизма =1/2 | |
| 10.1 | S(a,r,q)=E(a,r,q)=r | А3 |
| 10.2 | S(a,r,q)=qr; E(a,r,q)=(1-q)r | А3 |
Из этой таблицы видно, что в качестве оптимальной стратегии A1 и A2 выступают по 5 раз, стратегия А3 – 16 раз, а стратегия А4 – ни разу. n
Поэтому, если у лица, принимающего решение, нет серьезных возражений, то стратегию А3 можно считать оптимальной.
Список литературыВентцель Е.С. Исследование операций. М.: Советское радио, 1972.
Дубров А.М., Лагоша Б.А., Хрусталев Е.Ю. Моделирование рисковых ситуаций в экономике и бизнесе. М.: Финансы и статистика, 1999.
Князевская Н.В., Князевский В.С. Принятие рискованных решений в экономике и бизнесе. М.: ЭБМ – Контур, 1998.
Федосеев В.В. Экономико-математические методы и модели в маркетинге. М.: Финстатинформ, 1996.
Чернов В.А. Анализ коммерческого риска. М.: Финансы и статистика, 1998.
Исследование операций в экономике / Под ред. проф. Н.Ш. Кремера. М.: ЮНИТИ, 1
Похожие работы
... , способных нанести урон компании. Вместе с тем рисками можно управлять так же, как процессами производства или закупки материалов. Для того чтобы компания могла принимать обоснованные решения в условиях неопределенности, она должна выработать политику по управлению рисками. Управление рисками следует регламентировать специальным внутренним документом – программой по управлению рисками. Основная ...
... за собой её гибель, либо требующие подключения к процессу самоуправления суперсистемы иерархически высшего управления. Так соборный интеллект видится индивидуальному интеллекту с точки зрения достаточно общей теории управления; возможно, что кому-то всё это, высказанное о соборных интеллектах, представляется бредом, но обратитесь тогда к любому специалисту по вычислительной технике: примитивная ...
... . // Информатика и образование. -1994. - №4. 45. Подиновский В.В., Ногин В.Д. Паретооптимальные решения многокритериальных задач. - М.: Наука, 1982, - 256 с., ил. 46. Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр: Учебное пособие для университетов: / - М.: Высш. шк., Книжный дом "Университет", 1998. - 304с.: ил. 47. Программа курса информатики для начальной школы по ...
... из сторон преследует собственные цели, не всегда совпадающие друг с другом. Неопределенность такого рода при принятии решений относят к классу поведенческих неопределенностей. Теоретической основой нахождения оптимального решения в условиях неопределенности и конфликтных ситуаций является теория игр. Игра - это математическая модель процесса функционирования конфликтующих элементов систем, в ...



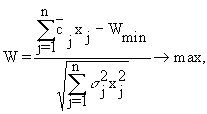
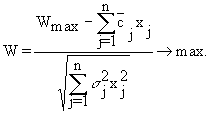
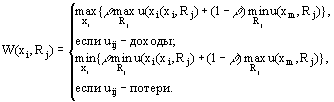
0 комментариев