Навигация
Структура группы симметрий системы независимости
9265
знаков
4
таблицы
2
изображения
2. Структура группы симметрий системы независимости
Итак, будем считать, что у нас зафиксирована система независимости 
на множестве E={e1,e2,,en}; RE-пространство, ассоциированное с E; P-многогранник системы независимости .
Так как 
, то для всякой симметрии со сдвигом h найдется такое H, что h=xH. Таким образом, группу S() можно разбить на непересекающиеся классы 
, где SH - класс симметрий многогранника P(), имеющих сдвиг xH. Это позволяет свести описание группы S() к описанию
.
Лемма 1. Пусть SH, a 1 - аффинное невырожденное преобразование пространства RE. Тогда 1SH, если и только если существует такое 2L(), что 1 = jj2.
Доказательство. Так как L() и SH являются подмножествами группы S(), то j1 = jj2S(). Очевидно, что j1 имеет сдвиг xH. Обратно, если j1 SH, то j2 = j-1j1S(), причем с нулевым сдвигом. Следовательно, j2L().
Таким образом, наличие какой-либо (любой) симметрии из SH позволяет с помощью группы L() найти весь класс SH.
Лемма 2. Пусть j - невырожденное преобразование пространства RE. Преобразование jSH тогда и только тогда, когда j=j1j2, где
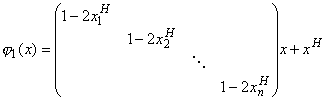
a j2 - H-отображение.
Доказательство. Прямыми вычислениями легко убедиться, что j1(xS) = xSH для любого SE, и j1-1=j1.
Если 2 - H-отображение, то для любого Iсуществует такой J, что 2(xI) = xJH. То есть 12(xI) = x(JH)H = xJ.
Следовательно, = 12 - симметрия многогранника P и jSH.
Если же jSH, то для любого I существует такой J, что (xI)=xJ. Следовательно, 2(xI) =1-1(xI) = 1-1(xJ) = 1(xJ) = xJH
Значит, 2 - H-отображение. Данная лемма дает возможность свести поиск представителя класса SH к поиску одного H-отображения. Причем, если H-отображений для данного H не существует, то SH=.
Поиск H-отображения существенно упрощается с помощью следующего предложения.
Предложение 1. Матрица H-отображения булева.
Доказательство. Так как {ej} для любого j{1n}, то ,по определению H-отображения, вектор (x{ej}), являющийся j-м столбцом матрицы отображения, булев, что и требовалось доказать.
Похожие работы
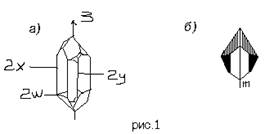
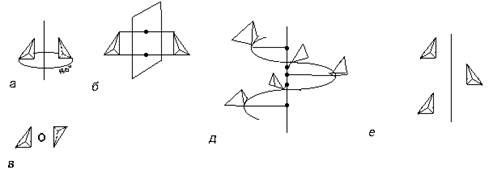
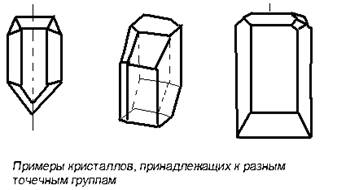
... , а затем и более фундаментального, одновременно и самого абстрактного (динамического) понимания симметрии. 2. 2.2.Симметрия кристаллов. Правильную, симметричную форму кристаллов издавна объясняли симметричным расположением атомов. Само существование атомов было еще гипотезой, но внешнее проявление стройного порядка заставляло предполагать внутреннюю причину. Быть может, правильные пирамиды, ...
... имеют достаточно четкое и правильное представление из собственного жизненного опыта, а формулировки которых являются слишком громоздкими. Выводы по § 1 1. Основные цели изучения темы «Объемы многогранников» в курсе стереометрии – развитие пространственных представлений учащихся, освоение способов вычисления практически важных величин и дальнейшее развитие логического мышления учащихся. ...
... . Реакции узлов более высокого уровня менее зависят от позиции и более устойчивы к искажениям. Структура Неокогнитрон имеет иерархическую структуру, ориентированную на моделирование зрительной системы человека. Он состоит из последовательности обрабатывающих слоев, организованных в иерархическую структуру (рис. 10.8). Входной образ подается на первый слой и передается через плоскости, ...
... , только если, например, нагреть кристалл так, чтобы он начал плавится. Порядок, закономерность, периодичность, симметрия расположения атомов - вот что характерно для кристаллов. Во всех кристаллах, во все твердых веществах частицы расположены правильным, четким строем, выстроены симметричным, правильным повторяющимся узором. Пока есть этот порядок существует твердое тело, кристалл. Нарушен ...
0 комментариев