Замкнутые инвариантные пространства функций на кватернионных сферах

И.А. Латыпов, Омский государственный университет, кафедра математического анализа,

Кватернионную сферу S4n-1 естественно рассматривать как однородное пространство группы Sp(n), действие задается левыми сдвигами. В связи с этим возникает задача описания замкнутых Sp(n)-инвариантных подпространств L p при и пространства непрерывных функций на сфере S4n-1, решенная в данной работе.

1. Предварительные сведения из теории алгебр Ли.

Группу Sp(n,C) зададим как множество матриц, удовлетворяющих условию StJS=J, где , 1n - единичная матрица размером . Дифференцированием получим соотношение XtJ+JX=0 для элементов алгебры Ли sp(n,C), а в блочном виде B=Bt, C=Ct. Выберем базис :

Подалгебра диагональных матриц будет картановской, - корневая система, где . Неприводимое представление алгебры Ли характеризуется своим старшим весом, лежащим в доминантной камере Вейля и имеющим целочисленные координаты. Размерность неприводимого представления, соответствующего старшему весу , вычисляется по формуле

где - полусумма положительных корней. Порядок будем считать лексикографическим. Более подробную информацию об алгебрах Ли можно найти в [2].

2. Представления алгебры Ли sp(n,C) в пространствах H(p,q).

Введем обозначения: Ok- пространство однородных полиномов степени однородности k, O(p,q) - пространство однородных полиномов степени однородности p и q по переменным z и соответственно (однородность понимается в вещественном смысле), Hk - пространство гармонических полиномов из Ok, H(p,q) - пространство гармонических полиномов из O(p,q).

Рассмотрим сначала алгебру u(n). Выберем ее базис над R в виде

Пусть - представление группы U(n) в Ok левыми сдвигами, . Дифференцированием функции s(exp(-tX)z) по t при t=0 получаем представление алгебры Ли u(n): где , , умножение - скалярное.

Задавая в u(n)C базис , получаем

Применим полученные формулы для представления алгебры sp(n,C)=sp(n)C:

где wi=zn+i.

H(p,q) - неприводимые компоненты представления u(n) и u(n)C, см. [4]. Значит, неприводимыми компонентами представления sp(n) и sp(n,C) будут некоторые подпространства H(p,q). Введем операторы ,

Проверка на базисных элементах дает

Предложение 1. Операторы L1 и L2 являются сплетающими для некоторых пар неприводимых представлений.

Найдем теперь старшие векторы из H(p,q), соответствующие неприводимым представлениям sp(n,C), они должны зануляться положительными операторами Dbij для всех i и j и Daij при i>j. Прямой проверкой получается

Предложение 2. При n>1 многочлен - старший вектор неприводимого представления sp(n,C) со старшим весом

Теорема 1. При n=1 H(p,q) неприводимо, а при n>1 .

Доказательство . Размерность H(p,q) равна

идею доказательства см. в [1].

Если n=1, вектор порождает неприводимое подпространство в H(p,q). Поскольку Da11S=(p+q)S, этот вектор соответствует старшему весу . Тогда 2x1 - единственный положительный корень, то есть H(p,q) неприводимо.

Пусть n>1. Осталось теперь показать, что

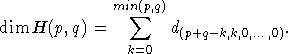
Эту формулу можно доказать по индукции, индуктивный переход делается от пары (p,q) к паре (p+1,q-1), а , что доказывает теорему.

Обозначим через инвариантную относительно вращений положительную борелевскую меру на S4n-1, для которой .

Следствие 1. Пространство является прямой суммой попарно ортогональных пространств P(p,q,r).

Следствие 2. Справедливы утверждения: a) В P(p1,q1,r1) и P(p2,q2,r2) при n>1 реализуются эквивалентные представления тогда и только тогда, когда p1+q1=p2+q2 и r1=r2.

b) При n=1 в H(p1,q2) и H(p2,q2) реализуются эквивалентные представления тогда и только тогда, когда p1+q1=p2+q2.

Пусть Ws,r и Ws - пространства линейных комбинаций векторов и соответственно с комплексными коэффициентами, . Введем также пространства и при n>1.

Следствие 3. Ws,r и Ws - пространства старших векторов неприводимых представлений со старшим весом и s соответственно. Сплетающие операторы неприводимых представлений можно выразить как многочлены от операторов L1 и L2.

Более подробные сведения из теории представлений можно найти, например, в [3].