В.П. Ильев, И.Б. Парфенова, Омский государственный университет, кафедра прикладной и вычислительной математики
1. Коалиционные игрыИгра есть математическая модель конфликта.Нас будут интересовать только такие конфликты, в которых допускается неограниченная кооперация его участников, вплоть до образования коалиций - устойчивых союзов для согласования действий в процессе выбора окончательного решения (исхода конфликта). Типичными примерами конфликтов являются выборы и законодательные процедуры.
Дж.фон Нейман и О.Моргенштерн [1] предложили следующую модель, наиболее адекватно отражающую кооперативную сущность подобных конфликтов.
Пусть ![]() - конечное множество, элементы которого называются игроками. Характеристической функцией (или коалиционной игрой) называется функция
- конечное множество, элементы которого называются игроками. Характеристической функцией (или коалиционной игрой) называется функция
|
| (1) |
Подмножества ![]() называются коалициями.
называются коалициями.
Действительное число v(S) можно интерпретировать как потенциальную силу коалиции S, то есть тот суммарный выигрыш, который гарантированно могут получить игроки из S, если объединятся в коалицию и будут действовать совместно.
Игрой в (0,1)-редуцированной форме (или в (0,1)-форме) называется игра, для которой v(N)=1 и ![]() . Игра в (0,1)-форме называется простой, если
. Игра в (0,1)-форме называется простой, если ![]() либо v(S)=0, либо v(S)=1. Простая игра характерна тем, что в ней любая коалиция является либо проигрывающей (если v(S)=0), либо выигрывающей (если v(S)=1).
либо v(S)=0, либо v(S)=1. Простая игра характерна тем, что в ней любая коалиция является либо проигрывающей (если v(S)=0), либо выигрывающей (если v(S)=1).
Примером простой игры является введенная Р.Боттом [2] и исследованная Д.Джиллисом [3] мажоритарная игра, названная ими (n,k)-игрой. Она определяется условием
|
| (2) |
где k - фиксированное целое число, ![]() .
.
В форме таких игр достаточно адекватно представляются различные модели голосования. Например, правилу простого большинства соответствует случай k=n/2, а правилу "двух третей" - квалифицированного большинства - случай k=2n/3.
Дележом в игре n лиц с характеристической функцией v называется вектор ![]() , удовлетворяющий условиям:
, удовлетворяющий условиям: ![]() Множество всех дележей в игре v обозначим I.
Множество всех дележей в игре v обозначим I.
Для простой игры n лиц множество дележей определяется условиями:
![]() На множестве всех дележей введем отношение предпочтения.
На множестве всех дележей введем отношение предпочтения.
Дележ x доминирует дележ ![]() , если найдется такая коалиция
, если найдется такая коалиция ![]() , что
, что ![]()
Легко видеть, что в простых играх доминирование возможно только по выигрывающим коалициям.
Дадим определение решения коалиционной игры n лиц по фон Нейману - Моргенштерну.
Множество дележей L называется внутренне устойчивым, если никакие два дележа из L не доминируют друг друга. Множество ![]() называется внешне устойчивым, если
называется внешне устойчивым, если ![]() . Множество дележей L называется NM-решением, если оно внутренне и внешне устойчиво.
. Множество дележей L называется NM-решением, если оно внутренне и внешне устойчиво.
В общем случае (для произвольной игры) задача нахождения NM-решения, а тем более всех NM-решений является очень трудной. К настоящему времени NM-решения найдены только для некоторых отдельных классов игр (подробнее см. обзор [4]).
Даже сравнительно простые игры могут иметь очень много NM-решений. Например, Р.Ботт [2] описал все симметричные решения (n,k)-игр, а Д.Джиллис [3] нашел огромное число разнообразных несимметричных решений таких игр.
Далее мы покажем, что любая (n,k)-игра может быть рассмотрена, как игра на матроиде специального вида. Рассмотрим другой класс игр на матроидах, являющийся обобщением (n,k)-игр, и опишем NM-решения игр этого класса.
2. Решения игр на матроидах разбиенийПусть ![]() - конечное множество,
- конечное множество, ![]() - семейство его подмножеств, обладающее следующими свойствами:
- семейство его подмножеств, обладающее следующими свойствами: ![]()
![]() Тогда пара
Тогда пара ![]() называется матроидом. Множества семейства
называется матроидом. Множества семейства ![]() называются независимыми множествами матроида M. Матроид называется дискретным, если
называются независимыми множествами матроида M. Матроид называется дискретным, если ![]() .
.
Важным классом матроидов являются так называемые матроиды разбиений. Рассмотрим какое-либо разбиение множества N, то есть ![]() для
для ![]() Заданы целые числа
Заданы целые числа ![]() Легко видеть, что тогда семейство
Легко видеть, что тогда семейство
![]() является семейством независимых множеств некоторого матроида. Этот матроид называется матроидом разбиения. Частным случаем матроида разбиения является (k-1)-однородный матроид (при p=1), семейство независимых множеств которого определяется как
является семейством независимых множеств некоторого матроида. Этот матроид называется матроидом разбиения. Частным случаем матроида разбиения является (k-1)-однородный матроид (при p=1), семейство независимых множеств которого определяется как
![]() где k - целое,
где k - целое, ![]()
С любым матроидом ![]() , отличным от дискретного, мы можем связать простую коалиционную игру n лиц, определив ее характеристическую функцию следующим образом:
, отличным от дискретного, мы можем связать простую коалиционную игру n лиц, определив ее характеристическую функцию следующим образом:
|
| (3) |
Такую игру будем называть игрой на матроиде.
Характеристическая функция игры на матроиде разбиения имеет вид:
|
| (4) |
Эту игру можно рассматривать как обобщение мажоритарной (n,k)-игры. Сама же (n,k)-игра является игрой на (k-1)-однородном матроиде.
Игру на матроиде разбиения (4) можно интерпретировать как игру с голосованием, когда голосование проводится по непересекающимся округам и выигрывающей считается коалиция, набравшая хотя бы в одном округе заданное число голосов.
NM-решение игры на матроиде разбиения будем строить, исходя из NM-решений (уже изученных Боттом и Джиллисом) игр на соответствующих (k-1)-однородных матроидах.
Пусть ![]() - матроид разбиения,
- матроид разбиения, ![]() .
.
Рассмотрим коалиционную игру (4) на матроиде разбиения M, а также для всех j рассмотрим мажоритарные (nj,kj)-игры
|
| (5) |
Фиксируем вектор ![]() такой, что
такой, что
|
| (6) |
Теорема. Пусть ![]() - какие-то NM-решения (nj,kj)-игр
- какие-то NM-решения (nj,kj)-игр ![]() . Тогда для любого
. Тогда для любого ![]() , удовлетворяющего (6), множество
, удовлетворяющего (6), множество
|
| (7) |
является NM-решением коалиционной игры (4) на матроиде разбиения M.
Очевидно, что векторы вида ![]() , где
, где ![]() , являются дележами в игре (4).
, являются дележами в игре (4).
Доказательство
1.Внутренняя устойчивость. Предположим, что в L найдутся такие дележи
![]() , что
, что ![]() по некоторой выигрывающей коалиции
по некоторой выигрывающей коалиции ![]() . Тогда
. Тогда ![]() - выигрывающая коалиция в игре vj и
- выигрывающая коалиция в игре vj и ![]() по коалиции
по коалиции ![]() . Это противоречит внутренней устойчивости множества Lj.
. Это противоречит внутренней устойчивости множества Lj.
2. Внешняя устойчивость. Рассмотрим произвольный делeж ![]() Докажем, что найдется такой делeж
Докажем, что найдется такой делeж ![]() , что
, что ![]() Заметим, что если бы
Заметим, что если бы ![]() то
то ![]() , и y не был бы дележом. Поэтому
, и y не был бы дележом. Поэтому ![]() Без ограничения общности можно считать, что
Без ограничения общности можно считать, что ![]() Возможны 2 случая:
Возможны 2 случая:
Случай 1. ![]() Рассмотрим вектор yj с компонентами вида
Рассмотрим вектор yj с компонентами вида ![]() . Тогда
. Тогда ![]() то есть yj - дележ в игре vj.
то есть yj - дележ в игре vj.
Если при этом окажется, что ![]() то сменим j (то есть рассмотрим другой номер j, для которого
то сменим j (то есть рассмотрим другой номер j, для которого ![]() . Такой обязательно существует, так как в противном случае
. Такой обязательно существует, так как в противном случае ![]() . Не может быть также, чтобы
. Не может быть также, чтобы ![]() и
и ![]() , так как это означает, что
, так как это означает, что ![]() ). Поэтому далее будем считать,что
). Поэтому далее будем считать,что ![]() Тогда
Тогда ![]() по некоторой выигрывающей коалиции
по некоторой выигрывающей коалиции ![]() Значит
Значит ![]() по коалиции Sj, где
по коалиции Sj, где ![]() .
.
Случай 2. ![]() Рассмотрим вектор yj с компонентами вида
Рассмотрим вектор yj с компонентами вида ![]() Заметим, что yj - не дележ в игре vj, так как
Заметим, что yj - не дележ в игре vj, так как ![]() Рассмотрим вектор zj с компонентами
Рассмотрим вектор zj с компонентами ![]() где
где ![]() Тогда
Тогда ![]() то есть zj - дележ в игре vj.
то есть zj - дележ в игре vj.
Если при этом окажется, что ![]() то
то ![]() , где xr - произвольный дележ из
, где xr - произвольный дележ из ![]() и
и ![]() по любой выигрывающей коалиции
по любой выигрывающей коалиции ![]() . Если же
. Если же ![]() , то
, то ![]() по некоторой выигрывающей коалиции
по некоторой выигрывающей коалиции ![]() Но тогда
Но тогда ![]() по коалиции Sj, где
по коалиции Sj, где ![]()
Пример. Голосование в Совете Безопасности ООН. Совет безопасности (СБ) состоит из 11 членов, из которых 5 - "Большая пятерка" имеют право вето. Для проведения решения за него должно быть подано 7 голосов при отсутствии вето.
Рассмотрим процедуру принятия решения в СБ как коалиционную игру, игроками которой являются страны-члены СБ. Множество N всех игроков естественным образом разделяется на два непересекающихся подмножества: N1-"Большая пятерка" и ![]() .
.
Будем считать успехом отклонение рассматриваемого проекта решения (т.е. отрицательное решение вопроса). Для простоты будем считать, что члены "Большой пятерки" не воздерживаются при голосовании. Тогда коалиция S противников проекта (в число которых мы включаем и воздержавшихся при голосовании) будет выигрывающей, если ![]() или
или ![]() . Характеристическая функция этой игры имеет вид:
. Характеристическая функция этой игры имеет вид:
![]()
Таким образом, мы имеем игру на матроиде разбиения ![]() , где
, где
![]()
Коэффициенты ![]() относительной важности элементов разбиения Nj могут быть получены на основании экспертных оценок либо априорных оценок игры (см. вектор Шепли [4]).
относительной важности элементов разбиения Nj могут быть получены на основании экспертных оценок либо априорных оценок игры (см. вектор Шепли [4]).
Например, Шепли и Шубик [5] утверждают, что 98,7 % силы обладает "Большая пятерка", а остальным шести членам СБ вместе взятым остается лишь 1,3 %. Если согласиться с этими оценками, то в NM-решении игры на матроиде, являющейся моделью системы голосования в СБ, следует принять ![]() .
.
Нейман Дж. фон, Моргенштерн О. Теория игр и экономическое поведение. М.: Наука, 1970.
Bott R. Symmetric solutions to majority games // Annals of Mathematical Studies. Princeton: Princeton Univ. Press, 1953. Vol.28. P.319-323.
Gilles D.B. Discriminatory and bargaining solutions to a class of symmetric n-person games // Там же. P.325-342.
Соболев А.И. Кооперативные игры // Проблемы кибернетики. М.: Наука, 1982. Вып.39. С.201-222.
Shapley L.S., Shubik M. A method for evaluiting the distribution of power in a commitee system // American Political Science Review. 1954. Vol.48. P.787-7
Похожие работы
... меньше веса любого "неотрицательного". К примеру, теорему 4 можно интерпретировать так: S0 и SA не содержат ни одного из наименьших по весу элементов. 3. Оценки погрешности градиентного алгоритма Лемма 2. Пусть - произвольная система независимости, - весовая функция, допускающая отрицательные веса. Если при этом веса всех элементов SA неотрицательны, то справедлива оценка (2). Доказательство. ...
... среди математиков, его разделяли А.Н.Колмогоров, И.М.Гельфанд, В.И.Арнольд, С.П.Новиков и др. Нельзя не восхищаться естественностью и внутренней стройностью математической работ Л.В. по двойственности линейного программирования и их экономической интерпретацией. 2. О математической экономике как области математики и о некоторых ее связях А) Связи линейного программирования с функциональным и ...
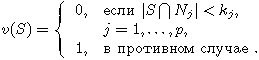
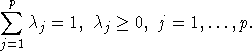
0 комментариев