Матрица A-1 - обратная для матрицы A, если
AA-1=A-1A=I
Для квадратной матрицы A обратная существует
тогда и только тогда, когда detA¹0.
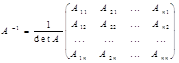
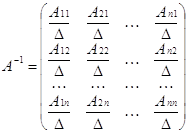
где Aij - алгебраические дополнения элэментов aij
матрицы A. Свойства: (A-1)-1=A,
(AB)-1=B-1A-1, detA-1=1/detA
В частности:
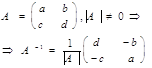
Решение квадратной системы:
Ax=b
если |A|¹0, то x=A-1b
Матричные уравнения.
XA=B Þ X=BA-1
AX=B Þ X=A-1B
Некоторые св-ва определителей:
1.* Величина определителя не изменится, если каждую
строку заменить столбцом с тем же номером.
2. Если матрица B получена из матрицы A
перестановкой двух каких-либо ее строк
(столбцов*), то detB=¾detA.
3. Общий множитель всех элементов произвольной
строки (столбца*) определителя можно вынести за
знак определителя.
4.* Определитель, содержащий две пропор-
циональные строки (столбца), равен нулю.
5. Определитель не меняется от прибавления к
какой-либо его строке (столбцу*) другой его строки
(столбца), умноженной на произвольное число.
6.* Если какая-либо строка (столбец) определителя
есть линейная комбинация других его строк
(столбцов), то определитель равен 0.
7. Если матрица имеет треугольный вид, то ее
определитель равен произведению элементов на
главной диагонали.
*-неизученные свойства.
Фундаментальная система решений.
Фундаментальной системой решений называется
система из (n-r) линейно независимых решений, где
n-число неизвестных, r-ранг матрицы системы:
ФСР: l1,l2,...,ln-r
ФСР может быть бесконечное множество.
Если l1,l2,...,ln-r-ФСР однородной системы, то
xоо = с1l1+с2l2+...+сn-r ln-r
xон = xоо + xчн
Метод Крамера:
Если D=0 и не все Dxj=0, то система несовместна.
Если D¹0, то система имеет единственное решение,
![]()
где Dxj - определитель, полученный заменой j-го
столбца в определителе системы столбцом
свободных членов.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.monax.ru/
Похожие работы
... так и ВּА, существует, так как матрицы согласованны: ·==·==; ·==·== = = АּВ=ВּА, т. е. данные матрицы коммутирующие. ЛЕКЦИЯ 2. ОПРЕДЕЛИТЕЛИ План 1. Определители квадратной матрицы и их свойства. 2. Теоремы Лапласа и аннулирования. Ключевые понятия Алгебраическое дополнение элемента определителя. Минор элемента определителя. ...
... матицы А существует противоположная –А, элементы которой отличаются от элементов А знаком, при этом А+( -А)=О. a(bА) = (ab)А = (aА)b. 6. (a+b)А = aА+bА. 7. a(А+В) = aА+aВ. 8. 1* А = А. 9. 0 * А = 0. Умножение матриц В матричной алгебре важную роль играет операция умножения матриц, это весьма своеобразная операция. Определение. Произведением матрицы А=(аij) размера и ...
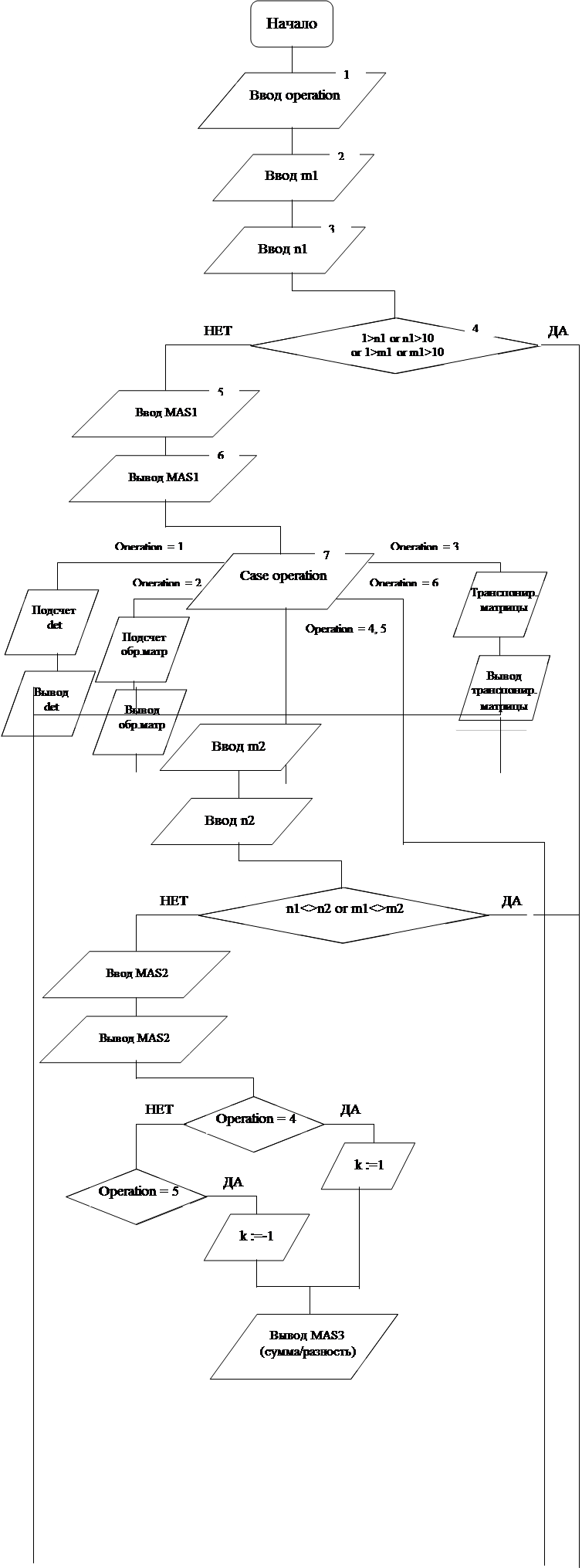
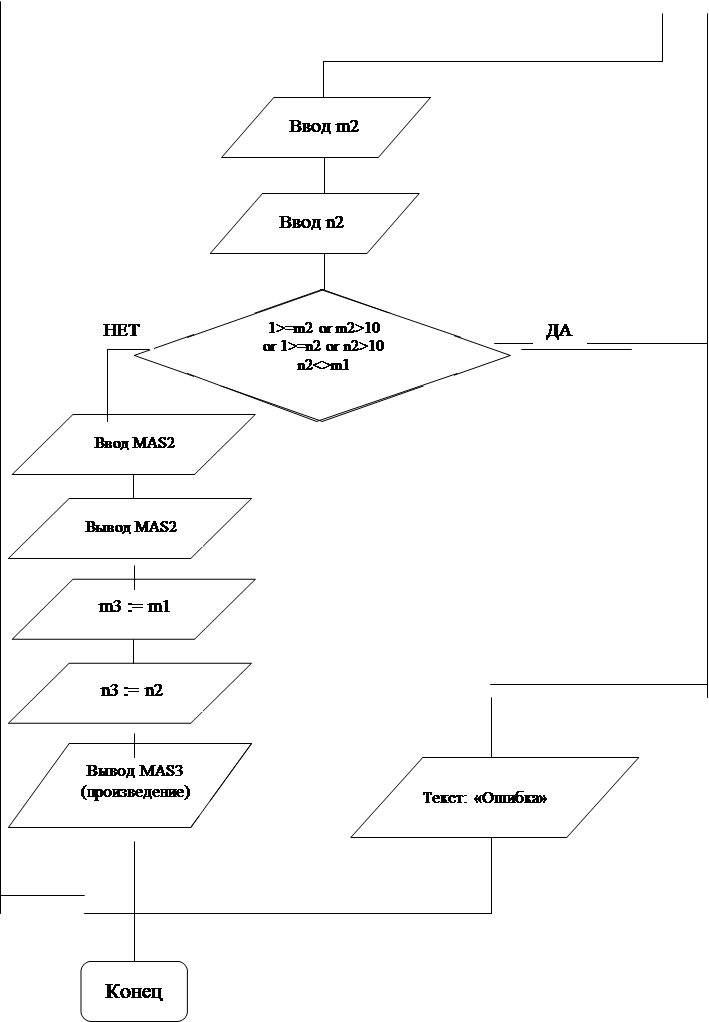
... «В» (в программе – MAS2), пользователю предлагается ввести ее размеры, как и при вводе матрицы «А», далее программа проверяет, возможно ли проведение выбранной операции над матрицами с введенными параметрами. Если операция невозможна, то на экран выводится сообщение об ошибке, и программа завершает работу. Иначе, операция выполняется, и ее результирующая матрица «С» (в программе – MAS3) выводится ...
... компонентами группы . наличие в групповой структуры позволяет высказать о компонентах ряд важных утверждений, отсутствующих в случае произвольного многообразия. 1.3.1 Теорема. Пусть --- алгебраическая группа матриц. Её компонента , содержащая единицу, единственна и является нормальной подгруппой. Остальные компоненты --- смежные классы по (в частности, они являются связными компонентами ...
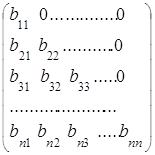
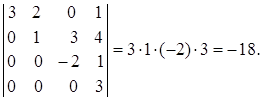
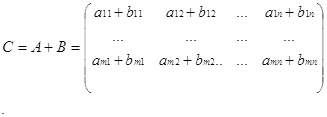

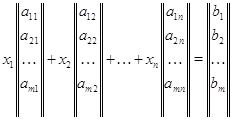
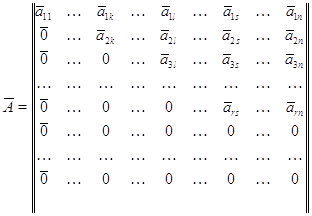
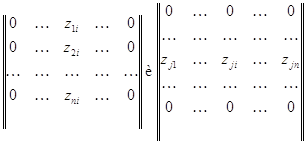
0 комментариев