Навигация
Алгебраические группы матриц
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
"Гомельский государственный университет
имени Франциска Скорины"
Математический факультет
Кафедра алгебры и геометрии
Курсовая работа
АЛГЕБРАИЧЕСКИЕ ГРУППЫ МАТРИЦ
Исполнитель:
студентка группы H.01.01.01 М-42
Мариненко В.В.
Научный руководитель:
доктор физико-математических наук,
профессор Скиба С.В.
Гомель 2003
Содержание
Введение
1. Алгебраические группы матриц
1.1 Примеры алгебраических групп матриц
1.2 О полугруппах
1.3 Компоненты алгебраической группы
1.4 О ![]() -группах
-группах
2 Ранг матрицы
2.1 Возвращение к уравнениям
2.2 Ранг матрицы
2.3 Критерий совместности
3 Линейные отображения. Действия с матрицами
3.1 Матрицы и отображения
3.2 Произведение матриц
3.3 Квадратные матрицы
Заключение
Список использованных источников
Введение
Множество ![]() матриц
матриц ![]() -ой степени над
-ой степени над ![]() будем рассматривать как аффинное пространство
будем рассматривать как аффинное пространство ![]() с имеющейся на ней полиномиальной топологией. Алгебраические группы матриц определяются как невырожденные части алгебраических множеств из
с имеющейся на ней полиномиальной топологией. Алгебраические группы матриц определяются как невырожденные части алгебраических множеств из ![]() , являющиеся группами относительно обычного матричного умножения. Простейший пример такой группы - общая линейная группа
, являющиеся группами относительно обычного матричного умножения. Простейший пример такой группы - общая линейная группа ![]() . В настоящем параграфе мы начнем систематическое изучение алгебраических матричных групп.
. В настоящем параграфе мы начнем систематическое изучение алгебраических матричных групп.
Все топологические понятия относятся к полиномиальной топологии; черта обозначает замыкание в ![]() , диез - замыкание в
, диез - замыкание в ![]() , бемоль - взятие невырожденной части, т. е.
, бемоль - взятие невырожденной части, т. е. ![]() - совокупность всех невырожденных матриц из
- совокупность всех невырожденных матриц из ![]() . Иногда, допуская вольность, мы употребляем для групп те же понятия, что и для подлежащих алгебраических множеств, - например, говорим об общих точках групп; это не должно вызывать недоразумений.
. Иногда, допуская вольность, мы употребляем для групп те же понятия, что и для подлежащих алгебраических множеств, - например, говорим об общих точках групп; это не должно вызывать недоразумений.
1. Алгебраические группы матриц
1.1 Примеры алгебраических групп матрицКлассические матричные группы - общая, специальная, симплектическая и ортогональная:
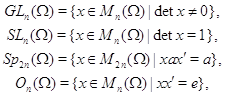
где ![]()
![]() - единичная матрица и штрих обозначает транспонирование.
- единичная матрица и штрих обозначает транспонирование.
Диагональная группа ![]() , группы клеточно-диагональных матриц данного вида. Треугольная группа
, группы клеточно-диагональных матриц данного вида. Треугольная группа ![]() (для определенности --- с нижним нулевым углом), унитреугольная группа
(для определенности --- с нижним нулевым углом), унитреугольная группа ![]() (треугольные матрицы с единичной диагональю), группы клеточно-треугольных матриц данного вида.
(треугольные матрицы с единичной диагональю), группы клеточно-треугольных матриц данного вида.
Централизатор произвольного множества из ![]() в алгебраической группе
в алгебраической группе ![]() , нормализатор замкнутого множества из
, нормализатор замкнутого множества из ![]() в
в ![]() .
.
Пересечение всех алгебраических групп, содержащих данное множество матриц ![]() из
из ![]() --- алгебраическая группа. Она обозначается
--- алгебраическая группа. Она обозначается ![]() и называется алгебраической группой, порожденной множеством
и называется алгебраической группой, порожденной множеством ![]() .
.
Каждую алгебраическую линейную группу из ![]() можно изоморфно --- в смысле умножения и полиномиальной топологии --- отождествить с замкнутой подгруппой из
можно изоморфно --- в смысле умножения и полиномиальной топологии --- отождествить с замкнутой подгруппой из ![]() в силу формулы
в силу формулы
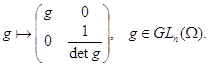
Такое отождествление позволяет при желании ограничиться рассмотрением только таких групп матриц, которые сами являются алгебраическими множествами (а не их невырожденными частями). Это дает другое оправдание тем вольностям в терминологии, которые упоминались в начале параграфа.
Множество всех матриц из ![]() , оставляющих инвариантной заданную невырожденную билинейную форму
, оставляющих инвариантной заданную невырожденную билинейную форму ![]() на
на ![]() .
.
Пусть ![]() --- алгебра над
--- алгебра над ![]() конечной размерности
конечной размерности ![]() (безразлично, ассоциативная или нет),
(безразлично, ассоциативная или нет), ![]() --- группа всех ее автоморфизмов. Фиксируя в
--- группа всех ее автоморфизмов. Фиксируя в ![]() какую-нибудь базу
какую-нибудь базу ![]() и сопоставляя автоморфизмам алгебры
и сопоставляя автоморфизмам алгебры ![]() их матрицы в этой базе, мы получим на
их матрицы в этой базе, мы получим на ![]() строение алгебраической группы. Действительно, пусть
строение алгебраической группы. Действительно, пусть
![]()
т. е. ![]() --- структурные константы алгебры
--- структурные константы алгебры ![]() . Пусть далее
. Пусть далее
![]()
где ![]() . Тогда
. Тогда ![]() задается в матричных координатах
задается в матричных координатах ![]() очевидными полиномиальными уравнениями, вытекающими из соотношений
очевидными полиномиальными уравнениями, вытекающими из соотношений
![]()
Указать в приведенных выше примерах определяющие уравнения, найти общую точку, если она есть.
В дальнейшем нам встретится еще много примеров и конструкций алгебраических матричных групп.
1.1.1 Если матричная группа ![]() содержит алгебраическую подгруппу
содержит алгебраическую подгруппу ![]() конечного индекса, то
конечного индекса, то ![]() сама алгебраическая.
сама алгебраическая.
Доказательство. Пусть ![]() - аннулятор группы
- аннулятор группы ![]() в
в ![]() ,
, ![]() - его корень в
- его корень в ![]() . Надо показать, что
. Надо показать, что ![]() . Пусть, напротив,
. Пусть, напротив, ![]() . Пусть
. Пусть ![]() - смежные классы
- смежные классы ![]() по
по ![]() . Для каждого
. Для каждого ![]() выберем многочлен
выберем многочлен
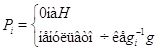
и положим
![]()
Очевидно, ![]() ,
, ![]() . Получили противоречие.
. Получили противоречие.
Пусть ![]() --- алгебраическая группа,
--- алгебраическая группа, ![]() ,
, ![]() --- подмножество и замкнутое подмножество из
--- подмножество и замкнутое подмножество из ![]() . Тогда множества
. Тогда множества
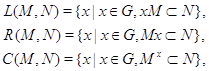
где ![]() , замкнуты. Если
, замкнуты. Если ![]() тоже замкнуто и
тоже замкнуто и ![]() --- общее поле квазиопределения для
--- общее поле квазиопределения для ![]() ,
, ![]() ,
, ![]() , то
, то ![]() ,
, ![]() ,
, ![]() квазиопределены над
квазиопределены над ![]() . В частности, если существует хотя бы одно
. В частности, если существует хотя бы одно ![]() с условием
с условием ![]() (соответственно,
(соответственно, ![]() ,
, ![]() ), то можно считать, что
), то можно считать, что ![]() (см. 7.1.5).
(см. 7.1.5).
Если на множестве ![]() выполняется теоретико-групповое тождество
выполняется теоретико-групповое тождество ![]() , то оно выполняется и на его замыкании
, то оно выполняется и на его замыкании ![]() . В частности, коммутативность, разрешимость, нильпотентность матричной группы сохраняются на ее замыкании в полиномиальной топологии.
. В частности, коммутативность, разрешимость, нильпотентность матричной группы сохраняются на ее замыкании в полиномиальной топологии.
Определим действие элементов из ![]() на рациональные функции из
на рациональные функции из ![]() ,
, ![]() , полагая
, полагая
![]()
Для каждого ![]() отображение
отображение ![]() (сдвиг аргумента) есть автоморфизм поля
(сдвиг аргумента) есть автоморфизм поля ![]() . Отображение
. Отображение ![]() есть изоморфизм полной линейной группы
есть изоморфизм полной линейной группы ![]() в группу автоморфизмов расширения
в группу автоморфизмов расширения ![]() .
.
Имеет место следующее предложение.
1.2.1 Все замкнутые (в полиномиальной топологии) полугруппы из ![]() являются группами. Более общно: замыкание
являются группами. Более общно: замыкание ![]() произвольной полугруппы
произвольной полугруппы ![]() --- группа. Более точно: если
--- группа. Более точно: если ![]() --- аннулятор
--- аннулятор ![]() в
в ![]() , то
, то ![]() совпадает с
совпадает с
![]()
Здесь вместо ![]() можно написать
можно написать ![]() .
.
Доказательство. Во-первых, ![]() и, значит,
и, значит, ![]() . Действительно, если
. Действительно, если ![]() ,
, ![]() и
и ![]() , то
, то ![]() , т. е.
, т. е. ![]() . Подпространство
. Подпространство ![]() многочленов из
многочленов из ![]() степени
степени ![]() отображается оператором
отображается оператором ![]() на себя, так как оно конечномерно, а опрератор обратим. Но тогда и всё
на себя, так как оно конечномерно, а опрератор обратим. Но тогда и всё ![]() отображается на себя, как объединение всех
отображается на себя, как объединение всех ![]() .
.
Во-вторых, ![]() , т. е.
, т. е. ![]() для каждого
для каждого ![]() . Действительно, пусть
. Действительно, пусть ![]() . По уже доказанному,
. По уже доказанному, ![]() . Найдём
. Найдём ![]() с условием
с условием ![]() . Тогда
. Тогда ![]() .
.
В-третьих, ![]() , т. е.
, т. е. ![]() для всех
для всех ![]() ,
, ![]() . Действительно,
. Действительно, ![]() . Предложение доказано.
. Предложение доказано.
Таким образом, теория алгебраических полугрупп из ![]() исчерпывается теорией алгебраических групп.
исчерпывается теорией алгебраических групп.
Отметим ещё одно полезное предложение.
1.2.2 Пусть алгебраическая группа ![]() неприводима, т. е.
неприводима, т. е. ![]() --- многообразие,
--- многообразие, ![]() --- густое подмножество, плотное в
--- густое подмножество, плотное в ![]() . Тогда каждый элемент
. Тогда каждый элемент ![]() является произведением двух элементов из
является произведением двух элементов из ![]() ; в частности, если
; в частности, если ![]() --- подгруппа, то она совпадает с
--- подгруппа, то она совпадает с ![]() .
.
Доказательство. Множества ![]() и
и ![]() тоже густые и плотные, поэтому пересечение
тоже густые и плотные, поэтому пересечение ![]() непусто (см. п. 8.2).
непусто (см. п. 8.2).
Если ![]() --- полугруппа из
--- полугруппа из ![]() , то
, то ![]() .
.
Пусть ![]() --- алгебраическая группа матриц. Невырожденные части компонент её подлежащего многообразия
--- алгебраическая группа матриц. Невырожденные части компонент её подлежащего многообразия ![]() называеются компонентами группы
называеются компонентами группы ![]() . наличие в
. наличие в ![]() групповой структуры позволяет высказать о компонентах ряд важных утверждений, отсутствующих в случае произвольного многообразия.
групповой структуры позволяет высказать о компонентах ряд важных утверждений, отсутствующих в случае произвольного многообразия.
1.3.1 Теорема. Пусть ![]() --- алгебраическая группа матриц. Её компонента
--- алгебраическая группа матриц. Её компонента ![]() , содержащая единицу, единственна и является нормальной подгруппой. Остальные компоненты --- смежные классы
, содержащая единицу, единственна и является нормальной подгруппой. Остальные компоненты --- смежные классы ![]() по
по ![]() (в частности, они являются связными компонентами группы
(в частности, они являются связными компонентами группы ![]() в полиномиальной топологии).
в полиномиальной топологии). ![]() --- единственная связная замкнутая подгруппа конечного индекса в
--- единственная связная замкнутая подгруппа конечного индекса в ![]() . Аннулятор
. Аннулятор ![]() компоненты
компоненты ![]() связан с аннулятором
связан с аннулятором ![]() всей группы
всей группы ![]() следующим образом:
следующим образом:
![]() для некоторого
для некоторого ![]() , зависящего от
, зависящего от ![]()
![]() , где
, где ![]() --- аннулятор единицы в
--- аннулятор единицы в ![]() ,
, ![]() --- некоторый многочлен из
--- некоторый многочлен из ![]() .
.
Доказательство. а) Пусть ![]() --- общее поле определения всех компонент
--- общее поле определения всех компонент ![]() группы
группы ![]() . Пусть
. Пусть ![]() ,
, ![]() содержат единицу
содержат единицу ![]() ,
, ![]() ,
, ![]() --- их независимые общие точки над
--- их независимые общие точки над ![]() и
и ![]() ,
, ![]() . Имеем специализации
. Имеем специализации
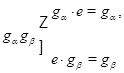
над ![]() , откуда
, откуда ![]() ,
, ![]() ,
, ![]() . Этим доказана единственность компоненты
. Этим доказана единственность компоненты ![]() .
.
б) Очевидно, что отображения
![]()
являются гомеоморфизмами пространства ![]() . Так как
. Так как ![]() инвариантна относительно них, то
инвариантна относительно них, то ![]() --- нормальная подгруппа группы
--- нормальная подгруппа группы ![]() .
.
в) Пусть ![]() . Тогда
. Тогда ![]() при фиксированном
при фиксированном ![]() --- снова все компоненты группы
--- снова все компоненты группы ![]() . В частности,
. В частности, ![]() ,
, ![]() . Этим доказано, что
. Этим доказано, что ![]() --- смежные классы
--- смежные классы ![]() по
по ![]() и, значит, связные компоненты группы
и, значит, связные компоненты группы ![]() .
.
г) Если ![]() --- связная замкнутая подгруппа группы
--- связная замкнутая подгруппа группы ![]() , то, предыдущему,
, то, предыдущему, ![]() . Если, кроме того,
. Если, кроме того, ![]() конечного индекса, то она той же размерности, что и
конечного индекса, то она той же размерности, что и ![]() , потому совпадает с
, потому совпадает с ![]() .
.
д) Для каждого ![]() возьмем многочлен
возьмем многочлен
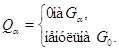
Пусть ![]() --- точка из
--- точка из ![]() , в которой
, в которой ![]() . Рассмотрим многочлен
. Рассмотрим многочлен
![]()
Он искомый. В самом деле, очевидно, ![]() . Оба включения справа налево очевидны (использовать простоту идеала
. Оба включения справа налево очевидны (использовать простоту идеала ![]() ). Остается доказать включение
). Остается доказать включение
![]()
Пусть ![]() ,
, ![]() . Имеем:
. Имеем:
![]()
Если ![]() , то
, то ![]() , если же
, если же ![]() ,
, ![]() , то
, то ![]() . В любом случае
. В любом случае ![]() . Следовательно,
. Следовательно, ![]() . Теорема доказана.
. Теорема доказана.
Мы видим, в частности, что для алгебраической группы неприводимость и связность в полиномиальной топологии --- одно и то же; в дальнейшем мы будем пользоваться только вторым термином, чтобы избежать путаницы с понятием матричной приводимости групп (к полураспавшейся форме).
Доказать, что связанная компонента единицы алгебраической группы содержится в любой замкнутой подгруппе конечного индекса.
Подгруппа ![]() алгебраической группы
алгебраической группы ![]() тогда и только тогда замкнута, когда замкнуто её пересечение со связной компонентой единицы
тогда и только тогда замкнута, когда замкнуто её пересечение со связной компонентой единицы ![]() .
.
<<Только тогда>> очевидно. <<Тогда>> вытекает из 9.1.9, если заметить, что
![]()
Конечная нормальная подгруппа ![]() связной алгебраической группы
связной алгебраической группы ![]() всегда лежит в центре
всегда лежит в центре ![]() .
.
![]()
В заключение отметим, что если в качестве универсальной области выбрано поле комплексных чисел ![]() , то в алгебраической группе можно рассматривать две топологии --- полиномиальную и евклидову. Ясно, что вторая тоньше первой, поэтому, в частности, евклидова связная компонента единицы содержится в полиномиальной связной компоненте. Можно было бы доказать и обратное, т. е. на самом деле связные компоненты комплексной алгебраической группы в обеих топологиях одни и те же. Этот результат становится неверным, если рассматривать
, то в алгебраической группе можно рассматривать две топологии --- полиномиальную и евклидову. Ясно, что вторая тоньше первой, поэтому, в частности, евклидова связная компонента единицы содержится в полиномиальной связной компоненте. Можно было бы доказать и обратное, т. е. на самом деле связные компоненты комплексной алгебраической группы в обеих топологиях одни и те же. Этот результат становится неверным, если рассматривать ![]() -порцию комплексной алгебраической группы (по поводу определения см. следующий пункт).
-порцию комплексной алгебраической группы (по поводу определения см. следующий пункт).
Пусть ![]() - поле. По определению, алгебраическая
- поле. По определению, алгебраическая ![]() -группа --- это группа матриц из
-группа --- это группа матриц из ![]() , выделяемая полиномиальными уравнениями с коэффициентами в
, выделяемая полиномиальными уравнениями с коэффициентами в ![]() . Иначе можно сказать, что это
. Иначе можно сказать, что это ![]() -порция, т. е. пересечение с
-порция, т. е. пересечение с ![]() , некоторой алгебраической группы, квазиопределенной над
, некоторой алгебраической группы, квазиопределенной над ![]() . Обычные алгебраические группы тоже можно трактовать как
. Обычные алгебраические группы тоже можно трактовать как ![]() -группы по отношению к некоторой большей универсальной области
-группы по отношению к некоторой большей универсальной области ![]() . В этом смысле понятие алгебраической
. В этом смысле понятие алгебраической ![]() -группы является более общим, так как от
-группы является более общим, так как от ![]() не требуется ни алгебраической замкнутости, ни бесконечной степени трансцендентности над простым полем.
не требуется ни алгебраической замкнутости, ни бесконечной степени трансцендентности над простым полем.
В свойствах алгебраических групп и ![]() -групп много общего. Имеется сандартный способ перехода от первых ко вторым --- посредством поля определения (в чём и состоит основное значение этого понятия). Нам не раз представится возможность продемонстрировать этот способ. В целом же
-групп много общего. Имеется сандартный способ перехода от первых ко вторым --- посредством поля определения (в чём и состоит основное значение этого понятия). Нам не раз представится возможность продемонстрировать этот способ. В целом же ![]() -группы в нашем изложении останутся на заднем плане, лишь иногда выходя на авансцену.
-группы в нашем изложении останутся на заднем плане, лишь иногда выходя на авансцену.
Многие результаты о ![]() -группах по формулировке и доказательству вполне аналогичны результатам об абсолютных алгебраических группах (в
-группах по формулировке и доказательству вполне аналогичны результатам об абсолютных алгебраических группах (в ![]() ) и опираются на сведения из алгебраической геометрии для
) и опираются на сведения из алгебраической геометрии для ![]() -множеств, (по определению, алгебраическое
-множеств, (по определению, алгебраическое ![]() -множество выделяется в
-множество выделяется в ![]() уравнениями с коэффициентами из
уравнениями с коэффициентами из ![]() ).
).
Похожие работы
... -x * y. Полем называется такое ассоциативное коммутативное кольцо с единицей k, в котором всякий ненулевой элемент обратим: . Таким образом, по определению в поле отсутствуют делители нуля. Кольцом называется множество с двумя алгебраическими операциями R (+, *), если: 0. Обратимыми называют те элементы кольца R, которые имеют обратные относительно операции умножения, множество R в данном случае ...
... гомоморфизм . K= - подгруппа Z и значит K=mZ для некоторого целого m. Отсюда следует, что H= . При этом и потому n=dm где d - целое. По теореме о гомоморфизме . Из доказанных теорем следует, что всякая подгруппа циклической группы циклична. Мы видим также, что для каждого целого d, делящего порядок n конечной циклической группы имеется и притом ровно одна подгруппа порядка d, то есть для ...
... размерность образа тоже равна 2n-2. Наконец, (M(n), L) - очевидно хорошая пара. Достаточно рассмотреть башню и использовать то, что tr(x)-1 - G-инвариант! Заметим еще, что в симплектическом случае характеристика поля произвольна. Пусть теперь G - любая группа типа B, D, C. Дословно повторяя доказательство теоремы 2 из [5], мы получим эпиморфизм , индуцированный (на остальных общих матрицах ...
... числа). Далее по формулам (2) последовательно находятся xn-1 , xn-2 ,…, x1 при i=n-1, n-2,...,1 соответственно. Таким образом, решение уравнений вида (1) описываем способом, называемым методом прогонки, сводится к вычислениям по трём простым формулам: нахождение так называемых прогоночных коэффициентов δi, λiпо формулам (3) при i=1,2,…,n (прямая прогонка) и затем неизвестных xi по ...
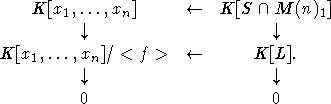
0 комментариев