Навигация
Розрахунок основних параметрів аналогової системи передачі
6. Розрахунок основних параметрів аналогової системи передачі.
Для вибору індексу частотної модуляції ми повинні порівняти значення ![]() та
та ![]() , де
, де 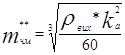 , (6.1)
, (6.1)
![]() - коефіцієнт амплітуди,
- коефіцієнт амплітуди,
![]() - припустиме відношення сигнал-завада на виході демодулятора.
- припустиме відношення сигнал-завада на виході демодулятора.
При частотній модуляції виграш знаходимо за формулою
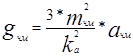 , (6.2)
, (6.2)
де ![]() - індекс частотної модуляції,
- індекс частотної модуляції,
![]() - коефіцієнт розширення смуги частот при ЧМ.
- коефіцієнт розширення смуги частот при ЧМ.
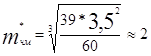 ,
,
![]() ,
,
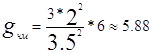 - виграш демодулятора за умови, що
- виграш демодулятора за умови, що ![]() перевищує порогове відношення сигнал-завада
перевищує порогове відношення сигнал-завада ![]() .
.
Залежність ![]() при будь-яких
при будь-яких ![]() , включаючи область границі, описується виразом, отриманим на основі імпульсної теорії границі [3,с.74..80]
, включаючи область границі, описується виразом, отриманим на основі імпульсної теорії границі [3,с.74..80]
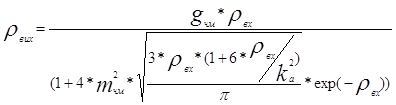
, (6.3)
Будуємо графіки залежностей![]() для значення
для значення ![]() , отриманого вище, та значень
, отриманого вище, та значень ![]() і
і ![]() [рис.5]. За отриманими залежностями визначаю значення
[рис.5]. За отриманими залежностями визначаю значення ![]() , за якого
, за якого ![]() дорівнює заданому
дорівнює заданому ![]() , а
, а ![]() знаходиться в області або трохи вище порога. На відповідній кривій вкажемо точку відповідну заданому
знаходиться в області або трохи вище порога. На відповідній кривій вкажемо точку відповідну заданому ![]() .
.
Таблиця 3.
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
| 0,733 | 2,257 | 5,656 | 11,85 | 20,45 | 29,69 | 38,13 | 45,54 | 52,22 | 58,49 |
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
| 2,93 | 9,02 | 22,61 | 47,37 | 81,77 | --- | --- | --- | --- | --- |
|
| 0,733 | 2,257 | 5,656 | 11,85 | 20,45 | 29,69 | 38,13 | 45,54 | 52,22 | 58,49 |
|
| 6,59 | 20,3 | 50,88 | 106,57 | --- | --- | --- | --- | --- | --- |
![]() - ширина спектру ЧМ сигналу.
- ширина спектру ЧМ сигналу.
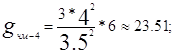
![]()
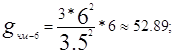
Знайдемо смугу пропускання каналу зв’язку :
![]() , (6.4)
, (6.4)
звідси отримуємо вираз для ![]()
![]()
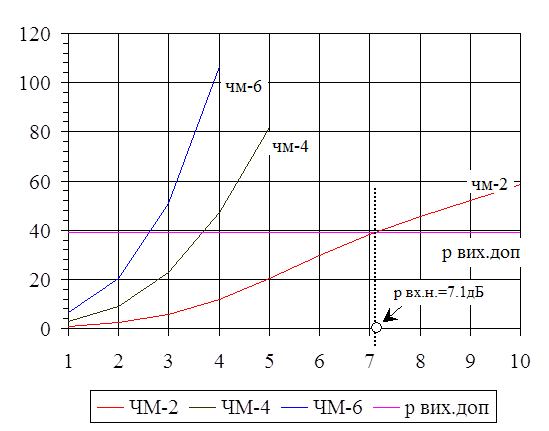
Рис.6 Графік залежності ![]() від
від ![]()
Зобразимо структурну схему аналогової системи передачі методом ЧМ.

Рис. 7 Структурна схема аналогової системи передачі методом ЧМ.
0 комментариев