Навигация
Сравнение выбранной схемы приемника с идеальным приемником Котельникова
2. Сравнение выбранной схемы приемника с идеальным приемником Котельникова
Обычно приемник получает на вход смесь передаваемого сигнала S(t) и помехи n(t). x(t)=S(t)+n(t). Как правило передаваемый сигнал S(t) – это сложное колебание, которое содержит кроме времени, множество других параметров (амплитуду, фазу, частоту и т.д.), т.е. сигнал S(t)=f(a,b,c,…t).Для передачи информации используется один, или группа этих параметров, и для приемника задача состоит в определении значений этих параметров в условиях мешающего действия помех.Если поставленная задача решается наилучшим образом, по сравнению с другими приемниками, то такой приемник можно назвать приемником, обеспечивающим потенциальную помехоустойчивость (идеальный приемник).
Схема идеального приемника

Рис 4
Данный приемник содержит два генератора опорных сигналов S1(t) и S2(t), которые вырабатывают такие-же сигналы, которые могут поступать на вход приемника, а также два квадратора и два интегратора и схему сравнения, которая выполняет функции распознавания и выбора, формируя на выходе сигналы S1 и S2. Т.к. данная схема идеального приемника, является приемником Котельникова, то как и многие другие приемники дискретных сигналов, она выдает на выходе сигналы, отличные от передаваемых. Для решения этой задачи, в схему включены выравнивающие устройства.
Как правило способ передачи информации (кодирование и модуляция) задан и задача сводится к поиску оптимальной помехоустойчивости, которую обеспечивают различные способы приема.
Под помехоустойчивостью системы связи подразумевается способность системы восстанавливать сигналы с заданной достоверностью. Предельно допустимая помехоустойчивость называется потенциальной. Сравнение потенциальной и реальной помехоустойчивости позволяет дать оценку качества приема данного устройства и найти еще не использованные ресурсы. Сведения о потенциальной помехоустойчивости приемника при различных способах передачи позволяют сравнить эти способы между собой и найти наиболее совершенные.
2.1. Рассмотрим и сравним амплитудную, частотную и фазовую (дискретные) модуляции.
ДИСКРЕТНАЯ АМПЛМТУДНАЯ МОДУЛЯЦИЯ (ДАМ).
Сигнал, поступающий на вход приемника (ДАМ) имеет следующий вид:
![]()
Вероятность ошибки зависит не от отношения мощности сигнала к мощности ошибки, а от отношения энергии сигнала к спектральной плотности помехи.
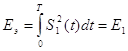 (Eэ – равна энергии первого сигнала)
(Eэ – равна энергии первого сигнала)
тогда аргумент функции Крампа Ф(x) равна ![]() , подставляя это выражение в формулу вероятности ошибки получим:
, подставляя это выражение в формулу вероятности ошибки получим:
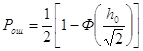 - вероятность ошибки для ДАМ. (4)
- вероятность ошибки для ДАМ. (4)
![]() S1
S1
ДАМ рис. 5
S2
На рис.5 представлена векторная диаграмма для ДАМ из нее видно, что расстояние между векторами S1 и S2 равно длине вектора S1.
ДИСКРЕТНАЯ ЧАСТОТНАЯ МОДУЛЯЦИЯ (ДЧМ).
Сигнал, поступающий на вход приемника, при данном виде модуляции имеет вид:
![]()
При частотной модуляции сигналы S1(t) и S2(t) являются взаимоортогональными, в связи с этим функция взаимной корреляции равна нулю. И так как амплитуды сигналов S1(t) и S2(t) равны, то Е1=Е2. В результате чего Еэ=2Е1, а аргумент функции Крампа будет равен: h0.
Поэтому подставляя эту величину в формулу вероятности получим:![]() - вероятность ошибки, при ДЧМ. (5)
- вероятность ошибки, при ДЧМ. (5)

![]() S1
S1
ДЧМ ![]() рис. 6
рис. 6
![]()
0 S2
На рис.6 представлена векторная диаграмма ДЧМ, на которой можно заметить, что расстояние между векторами (взаимоортогональные сигналы) равно ![]() . Заметим, что по сравнению с ДАМ, мы получаем двойной выигрыш по мощности.
. Заметим, что по сравнению с ДАМ, мы получаем двойной выигрыш по мощности.
ДИСКРЕТНАЯ ФАЗОВАЯ МОДУЛЯЦИЯ (ДФМ).
При ДФМ сигнал, поступающий на вход приемника имеет следующий вид:
![]()
В данном случае аргумент функции Крампа будет равен: ![]()
Поэтому подставляя эту величину в формулу вероятности ошибки получим:
![]() (6)
(6)
![]() S1
S1
![]()
![]() ДФМ 0 рис.7
ДФМ 0 рис.7
S2
Из приведенной векторной диаграммы видно, что расстояние между векторами сигналов равно 2S1. Энергия пропорциональна квадрату разности сигналов.
Заметим, что по сравнению с ДАМ мы получим четырехкратный выигрыш по мощности.
Следует уточнить, что приведенные данные о энергии сигналов ДАМ, ДЧМ и ДФМ относятся к пиковым мощностям этих сигналов. В этом смысле при переходе от ДЧМ к ДАМ мы имеем двукратный выигрыш в пиковой мощности, однако при ДАМ сигналы имеют пассивную паузу, т.е. мощность сигналов в паузе равна нулю, поэтому по потребляемой передатчиком мощности, кроме проигрыша по мощности, имеется еще и двукратный выигрыш. С учетом этого, при переходе от ДЧМ к ДАМ проигрыш по мощности компенсируется двукратным выигрышем за счет пассивной паузы ДАМ, в результате чего по потребляемой мощности эти сигналы оказываются равноценными, однако при ДАМ трудно установить необходимый порог в сравнивающем устройстве, а при приеме сигналов ДЧМ регулировка порога не требуется, в связи с этим свойством ДЧМ применяется чаще, чем ЧАМ.
Вероятность ошибки зависит от вероятности некорректного приема сигналов S1 и S2, но при применении приемника Котельникова предполагается что канал связи – симметричный, т.е. совместные вероятности передачи и приема сигналов
S1 и S2 равны. Исходя из этого запишем формулу вероятности ошибки: 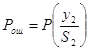 (7)
(7)
Возьмем формулу 7 за основу для определении вероятности ошибки в приемнике Котельникова.
Предположим, что нам известно, что на вход приемника поступает сигнал S1(t). в этом случае используя правило приемника Котельникова, в котором должно выполняться следующее неравенство:
![]() (8)
(8)
При сильной помехе знак неравенства может измениться на противоположный, в результате чего вместо сигнала S1(t) на вход может поступить сигнал S2(t), т.е. произойдет ошибка. Поэтому вероятность ошибки можно рассматривать, как вероятность изменения знака неравенства (8). Подставляя вместо x(t)=S1(t)+n(t). Преобразовывая получаем:
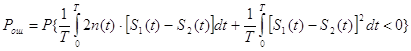 (8)
(8)
Вероятность ошибки в приемнике Котельникова, выраженная, через эквивалентную энергию Еэ, которая представляет собой разность сигналов S1(t) и S2(t) и будет определяться формулой:
![]()
Формулы вероятности ошибки для ДАМ, ДЧМ и ДФМ. Приведены соответственно: 6, 5, 4.
Похожие работы
... работы необходимо начинать с приобретения методических руководств к курсовой работе Ниеталина Ж.Н. и Ниеталиной Ж.Ж. «Электрлiк байланыс теориясы» выпущенной в Алма-Ате в 1999 году, Ниеталина Ж.Н. и Ниеталиной Ж.Ж. «Теория электрической связи» учебное пособие к курсовой работе. Алма-Ата 2001г., а также учебное пособие Зюко А.Г. и др. «Теория передачи сигналов» – М.; «Связь» 1988г., «Теория ...
... Вид сигнала при модуляции прямоугольными импульсами со скважностью 2: рис. 3 Для отыскания спектра сигнала ДФМ запишем: Спектры сигналов для различных значений: Рис. 4 2.3 Расчет вероятности ошибки на выходе приемника. Вероятность ошибки на выходе приемника определяется формулой где Ф() – функция Крампа q – отношение мощности сигнала к ...
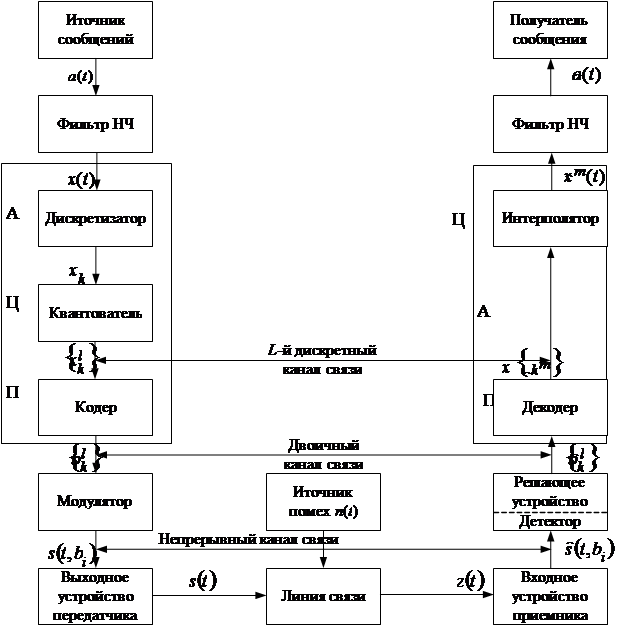
... форму представления информации. Часто сообщения подают в виде изменяющегося во времени тока или напряжения, которые отображают переданную информацию. Рисунок 1.1 – Структурная схема цифровой системы связи В передатчике (ИС) сообщения сначала фильтруется с целью ограничения его спектра некоторой верхней частотой fВ. Это необходимо для эффективного представления отклика ФНЧ x(t) в виде ...
... обратный процесс - преобразование цифрового сигнала в аналоговый. В данной курсовой работе необходимо рассчитать технические характеристики цифровой системы связи. . 1. СТРУКТУРНАЯ СХЕМА СИСТЕМЫ ЦИФРОВОЙ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ. Для передачи непрерывных сообщений можно воспользоваться дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, то есть в ...
0 комментариев