Сравнение выбранной схемы приемника с идеальным приемником Котельникова
Преобразование приемника Котельникова применительно к фазовой модуляции
Передача аналоговых сигналов методом ИКМ
Статистическое (эффективное) кодирование
Статистическое кодирование элементов сообщения
Пропускная способность канала связи
Навигация
Статистическое кодирование элементов сообщения
Теории электрической связи: Расчет приемника, оптимальная фильтрация, эффективное кодирование
42211
знаков
5
таблиц
6
изображений
5.1. Статистическое кодирование элементов сообщения
Осуществим статистическое кодирование трехбуквенных комбинаций, состоящих из элементов двоичного кода 1 и 0: 000,001,010,011,100,101,110,111. Для кодирования воспользуемся алгоритмом неравномерного кодирования Хаффмана. Для этого вычислим вероятности этих комбинаций и расположим их в порядке убывания вероятностей.
| Символы | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 |
| Кодовые комбинации | 111 | 110 | 101 | 011 | 100 | 010 | 001 | 000 |
| Вероятности | 0,729 | 0,081 | 0,081 | 0,081 | 0,009 | 0,009 | 0,009 | 0,001 |
Составим сводную таблицу ветвления кодовых комбинаций.
Табл.1.
| Символ и нач. вероятность | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Z1 | 0.729 | 0.729 | 0.729 | 0.729 | 0.729 | 0.729 | 0.729 | 1 |
| Z2 | 0.081 | 0.081 | 0.081 | 0.081 | 0.109 | 0.162 | 0.271 | |
| Z3 | 0.081 | 0.081 | 0.081 | 0.081 | 0.081 | 0.109 | ||
| Z4 | 0.081 | 0.081 | 0.081 | 0.081 | 0.081 | |||
| Z5 | 0.009 | 0.01 | 0.018 | 0.028 | ||||
| Z6 | 0.009 | 0.009 | 0.01 | |||||
| Z7 | 0.009 | 0.009 | ||||||
| Z8 | 0.001 | |||||||
Согласно таблице 1 составляем граф кодового дерева, из точки · с вероятностью 1 направляем две ветви с большей вероятностью – влево, с меньшей – вправо. Такое ветвление продолжаем до тех пор, пока не дойдем до вероятности р каждой буквы.
Составим граф кодового дерева.
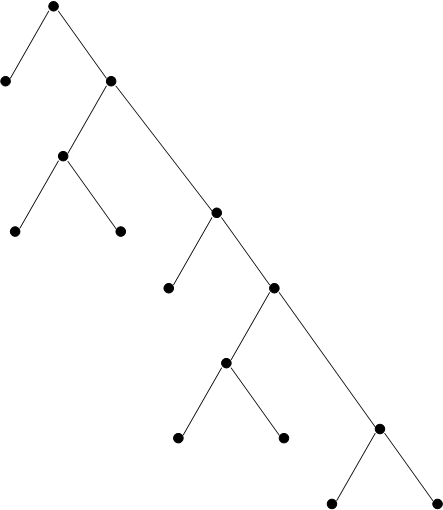
Рис. 7
На основании графа кодового дерева выписываем кодовые комбинации.
| Символы | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 |
| Кодовые комбинации | 1 | 011 | 010 | 001 | 00011 | 00010 | 00001 | 00000 |
Определяем среднюю длину полученных кодовых комбинаций:
Полученные комбинации кода фактически содержат информацию о трех элементах сигнала, поэтому разделив 
на 3 получим среднюю длину новых комбинаций в расчете на одну букву первоначального двоичного кода.
в результате получили среднюю скорость, меньше t. Это и есть эффект статистического кодирования.
Найдем производительность источника после кодирования.
это позволило получить выигрыш производительности источника 0,533 раза.
Похожие работы
... работы необходимо начинать с приобретения методических руководств к курсовой работе Ниеталина Ж.Н. и Ниеталиной Ж.Ж. «Электрлiк байланыс теориясы» выпущенной в Алма-Ате в 1999 году, Ниеталина Ж.Н. и Ниеталиной Ж.Ж. «Теория электрической связи» учебное пособие к курсовой работе. Алма-Ата 2001г., а также учебное пособие Зюко А.Г. и др. «Теория передачи сигналов» – М.; «Связь» 1988г., «Теория ...
... Вид сигнала при модуляции прямоугольными импульсами со скважностью 2: рис. 3 Для отыскания спектра сигнала ДФМ запишем: Спектры сигналов для различных значений: Рис. 4 2.3 Расчет вероятности ошибки на выходе приемника. Вероятность ошибки на выходе приемника определяется формулой где Ф() – функция Крампа q – отношение мощности сигнала к ...
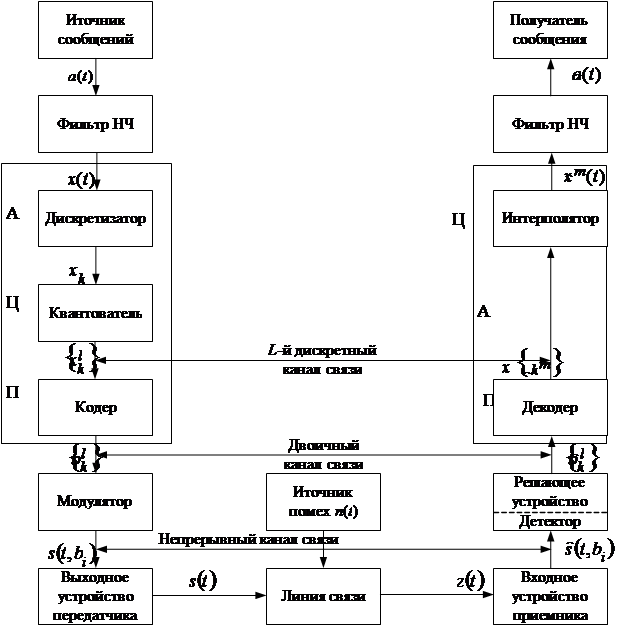
... форму представления информации. Часто сообщения подают в виде изменяющегося во времени тока или напряжения, которые отображают переданную информацию. Рисунок 1.1 – Структурная схема цифровой системы связи В передатчике (ИС) сообщения сначала фильтруется с целью ограничения его спектра некоторой верхней частотой fВ. Это необходимо для эффективного представления отклика ФНЧ x(t) в виде ...
... обратный процесс - преобразование цифрового сигнала в аналоговый. В данной курсовой работе необходимо рассчитать технические характеристики цифровой системы связи. . 1. СТРУКТУРНАЯ СХЕМА СИСТЕМЫ ЦИФРОВОЙ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ. Для передачи непрерывных сообщений можно воспользоваться дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, то есть в ...
0 комментариев