Навигация
Память для данных элементарных типов
3. Память для данных элементарных типов
Типы данных исходной программы должны быть отображены на
типы данных машины. Для некоторых типов это будет соответствием
один к одному ( целые, вещественные и т. д. ), для других могут
понадобиться несколько машинных слов. Можно отметить следующее:
1) Целые переменные обычно содержатся в одном слове или
ячейке области данных; значение хранится в виде стандартного
внутреннего изображения целого числа в машине.
2) Вещественные переменные обычно содержатся в одном слове.
Если желательна большая точность, чем возможно представить в
одном слове, то может быть употреблен машинный формат двойного
слова с плавающей запятой. В машинах, где отсутствует формат с
плавающей запятой, могут быть употреблены два слова - одно
для показателя степени, второе для ( нормализованной ) мантиссы.
Операции с плавающей запятой в этом случае должны выполняться с
помощью подпрограмм.
3) Булевы или логические переменные могут содержаться в
одном слове, причем нуль изображает значение FALSE, а не нуль или
1 -- значение TRUE. Конкретное представление для TRUE и FALSE
определяется командами машины, осуществляющими логические
операции. Для каждой булевой переменной можно также использовать
один бит и разместить в одном слове несколько булевых переменных
или констант.
4) Указатель - это адрес другого значения ( или ссылка на
него ). В некоторых случаях бывает необходимо представлять
указатель в двух последовательных ячейках; одна ячейка содержит
ссылку на описатель или является описателем текущей величины,
на которую ссылается указатель, в то время как другая указывает
собственно на значение величины. Это бывает необходимо в случае
когда во время компиляции невозможно определить для каждого
использования указателя тип величины, на которую он ссылается.
4. Память для массивов
Мы предполагаем, что каждый элемент массива или вектора
занимает в памяти одну ячейку. Случай большего числа ячеек
полностью аналогичен.
Векторы
Элементы векторов ( одномерных массивов ) обычно помещаются
в последовательных ячейках области данных в порядке возрастания
или убывания адресов. Порядок зависит от машины и ее системы
команд.
Мы предполагаем, что используется стандартный возрастающий
порядок, т. е. элементы массива, определенного описанием
ARRAY А [1:10], размещаются в порядке А [1], А [2], ..., А [10].
Матрицы
Существует несколько способов размещения двумерных массивов.
Обычный способ состоит в хранении их в области данных по строкам
в порядке возрастания, т. е. ( для массива, описанного как
ARRAY А [1:M, 1:N], в порядке
А [1, 1], А [1, 2], ..., А [1, N],
А [2, 1], А [2, 2], ..., А [2, N],
...
А [M, 1], А [M, 2], ..., А [M, N].
Вид последовательности показывает, что элемент А[i, j] находится
в ячейке с адресом ADDRESS ( A[1, 1] ) + (i-1)*N + (j-1) который
можно записать так: ( ADDRESS ( A[1, 1] ) - N - 1 ) + ( i*N + j )
Первое слагаемое является константой, и его требуется вычислить
только один раз. Таким образом, для определения адреса А[i, j]
необходимо выполнить одно умножение и два сложения.
Второй метод состоит в том, что выделяется отдельная область
данных для каждой строки и имеется вектор указателей для этих
областей данных. Элементы каждой строки размещаются в соседних
ячейках в порядке возрастания. Так, описание ARRAY А [1:M, 1:N]
порождает
┌────────────────────────┐ ┌─────────────────────┐
│ Указатель на строку 1 ├─────────┤ A[1, 1] ... A[1, N] │
├────────────────────────┤ └─────────────────────┘
│ Указатель на строку 2 ├───────┐ ┌─────────────────────┐
├────────────────────────┤ └─┤ A[2, 1] ... A[2, N] │
│ ... │ └─────────────────────┘
├────────────────────────┤ ┌─────────────────────┐
│ Указатель на строку M ├─────────┤ A[M, 1] ... A[M, N] │
└────────────────────────┘ └─────────────────────┘
Вектор указателей строк хранится в той области данных, с которой
ассоциируется массив, в то время как собственно массив хранится
в отдельной области данных. Адрес элемента массива А[i, j] есть
CONTENTS(i-1) + (j-1).
Первое преимущество этого метода состоит в том, что при
вычислении адреса не нужно выполнять операцию умножения. Другим
является то, что не все строки могут находиться в оперативной
памяти одновременно. Указатель строки может содержать некоторое
значение, которое вызовет аппаратное или программное прерывание
в случае, если строка в памяти отсутствует. Когда возникает
прерывание, строка вводится в оперативную память из на место
другой строки.
Если все строки находятся в оперативной памяти, то массив
требует больше места, поскольку необходимо место и для вектора
указателей.
Когда известно, что матрицы разреженные ( большинство
элементов - нули ), используются другие методы. Может быть
применена схема хеш-адресации, которая базируется на значениях i
и j элемента массива А[i, j] и ссылается по хеш-адресу на
относительно короткую таблицу элементов массива. В таблице
хранятся только ненулевые элементы матрицы.
Многомерные массивы
Мы рассмотрим размещение в памяти и обращение к
многомерным массивам, описанным, следующим образом:
ARRAY A[L1:U1, L2:U2, ..., Ln:Un]
Метод заключается в обобщении первого метода, предложенного для
двумерного случая; он также применим и для одномерного массива.
Подмассив A[i,*, ..., *] содержит последовательность
A[L1,*, ..., *], A[L1+1,*, ..., *], и т.д. до A[U1,*, ..., *].
Внутри подмассива A[i,*, ..., *] находятся подмассивы
A[i,L2,*, ..., *], A[i,L2+1,*, ..., *], ... и A[i,U2,*, ..., *].
Это повторяется для каждого измерения. Так, если мы продвигаемся
в порядке возрастания по элементам массива, быстрее изменяются
последние индексы:
┌───────────────────────────────────────┐ ┌─────────┐ ┌───────┐
│ подмассив A[L1] │ │ A[L1+1] │ │ A[U1] │
│ ┌────────┐ ┌──────────┐ ┌────────┐│ │ │ │ │
│ │A[L1,L2]│ │A[L1,L2+1]│ ... │A[L1,U2]││ │ │ ... │ │
│ └────────┘ └──────────┘ └────────┘│ │ │ │ │
└───────────────────────────────────────┘ └─────────┘ └───────┘
Вопрос заключается в том, как обратиться к элементу
A[i,j,k, ..., l,m]. Обозначим
d1 = U1-L1+1, d2 = U2-L2+1, ..., dn = Un-Ln+1.
То есть d1 есть число различных значений индексов в i-том
измерении. Следуя логике двумерного случая, мы находим начало
подмассива A[i,*, ..., *]
BASELOC + (i-L1)*d2*d3*...*dn
Где BASELOC - адрес первого элемента A[L1,L2,...,Ln], а
d2*d3*...*dn - размер каждого подмассива A[i,*,...,*]. Начало
подмассива A[i,j,*,...,*] находится затем добавлением
(j-L2)*d3*...*dn к полученному значению.
Действуя дальше таким же образом, мы окончательно получим:
BASELOC + (i-L1)*d2*d3*...*dn + (j-L2)*d3*...*dn
+ (k-L3)*d4*...*dn + ... + (i - Ln-1)*dn + m - Ln
Выполняя умножения, получаем CONST_PART + VAR_PART, где
CONST_PART = BASELOC - ((...(L1*d2+L2)*d3+L3)*d4+...+Ln-1)*dn+Ln)
VAR_PART = (...((i*d2)+j)*d3+...+1)*dn + m
Значение CONST_PART необходимо вычислить только 1 раз и
запомнить, т.к. оно зависит лишь от нижних и верхних границ
индексов и местоположения массива в памяти. VAR_PART зависит от
значений индексов i,j,...,m и от размеров измерений d2,d3,...,
dn. Вычисление VAR_PART можно представить в более наглядном виде:
VAR_PART = первый индекс (i)
VAR_PART = VAR_PART*d2 + второй индекс (j)
VAR_PART = VAR_PART*d3 + третий индекс (k)
.....
VAR_PART = VAR_PART*dn + n-й индекс (m)
Информационные векторы
В некоторых языках верхняя и нижняя границы массивов известны
во время трансляции, поэтому компилятор может выделить память для
массивов и сформировать команды, ссылающиеся на элементы массива,
┌────┬────┬────┐
│ L1 │ U1 │ d1 │
├────┼────┼────┤
│ L2 │ U2 │ d2 │
│ . │ . │ . │ Описание массива
│ . │ . │ . │ A[L1:U1,...,Ln:Un]
│ . │ . │ . │
│ Ln │ Un │ dn │
├────┼────┴────┤
│ n │CONSTPART│
├────┴─────────┤
│ BASELOC │
└──────────────┘
Рис. . Информационный вектор для массива
используя верхние и нижние границы и постоянные значения d1,d2,..
.,dn. В других языках это невозможно т.к. границы могут
вычисляться во время счета. Поэтому нужен описатель для массива,
содержащий необходимую информацию. Этот описатель для массива
называется допвектор ( dope vector ) или информационный вектор.
Информационный вектор имеет фиксированный размер, который
известен при компиляции, следовательно, память для него может
быть отведена во время компиляции в области данных, с которой
ассоциируется массив. Память для самого массива не может быть
отведена до тех пор, пока во время счета не выполнится вход в
блок, и котором описан массив. При входе в блок вычисляются
границы массива и производится обращение к программе
распределения памяти для массивов. Здесь же вносится в
информационный вектор необходимая информация.
Какая информация заносится в информационный вектор? Для
предложенной выше n-мерной схемы нам как минимум нужны d2,...dn
и CONST_PART. Если перед обращением к массиву нужно проверять
правильность задания индексов, то следует также занести в
информационный вектор значения верхних и нижних границ.
Похожие работы
... 12 Библиографический список................................................................. 15 Введение Целью работы является демонстрация работы с динамической памятью на примере программ разработанных к заданиям 2, 6, 8, 10, 12, 14, 16 из методического указания [1]. Динамическое распределение памяти предоставляет программисту большие возможности при обращении к ресурсам памяти в ...
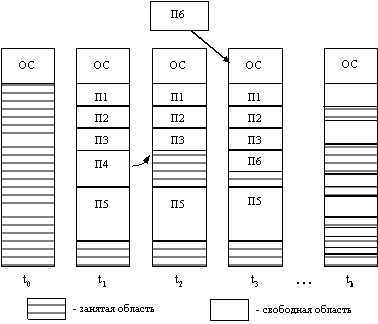
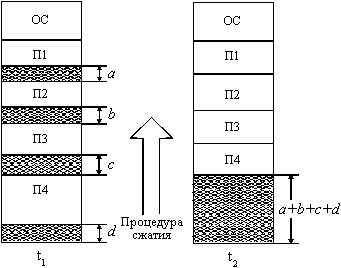
... задачи П4 место загружается задача П6, поступившая в момент t3. Рис. 2.10. Распределение памяти динамическими разделами Задачами операционной системы при реализации данного метода управления памятью является: ведение таблиц свободных и занятых областей, в которых указываются начальные адреса и размеры участков памяти, при поступлении новой задачи - анализ запроса, просмотр ...
... .) В системах, в которых страницы инструкций (в противоположность страницам данных) являются реентерабельными, бит изменения никогда не устанавливается. 2. Разработка алгоритма управления оперативной памятью Ниже приведён алгоритм управления оперативной памятью в системе Linux. В основе всего лежат страницы памяти. В ядре они описываются структурой mem_map_t. typedef struct page { /* ...
... новые следы памяти могут поступать в активном или неактивном состоянии. Именно это свойство лежит в основе исключительно важного феномена — так называемого латентного обучения. Концепция состояний памяти свободна от условного деления на кратковременную и долговременную и потому может объяснять феномены, которые остаются непонятными с точки зрения временного подхода к организации памяти. То, что ...
0 комментариев